
非线性方程求根 用数值方法求非线性方程的根,通常分两步进行: 第一步:对根进行隔离,找出隔根区间,或在隔根区间内 确定一个解的近似值x; 第二步:逐步逼近,利用近似解x(或隔根区间) 通过迭代算法得到更精确的近似解, 设fx)=0的根为x*,通过迭代计算,产生序列: x0今x1今x2今…今Xm 只须 limx=x n→∞ 1/14
1/14 第一步: 对根进行隔离,找出隔根区间,或在隔根区间内 确定一个解的近似值x0; 设f(x) = 0的根为 x* ,通过 , 产生序列: x0 x1 x2 ··· xn ········· 用 求非线性方程的根,通常分两步进行: 第二步:逐步逼近,利用近似解x0 (或隔根区间) 通过迭代算法得到更精确的近似解. * lim x n x n 只须 非线性方程求根

一、二分法 定理2.1设函数fc)在区间a,b上连续,且 f(a)f(b)<0, 则方程f(x)=0在区间(a,b)内至少有一个根。 基本思想: 对有根区间[a,b]逐次分半,直到满足精 度要求 。 b2 br X2 Xo a a 2/14
2/14 一、二分法 设函数 f (x)在区间[a,b]上连续,且 f(a)f(b)< 0, 则方程f(x)= 0 在区间(a,b)内至少有一个根。 基本思想: 对有根区间[a,b]逐次分半,直到满足精 度要求

二分法计算过程中产生区间序列 [ak,bJ(k=1,2,3,…) 显然有 [a,b]a,biaz,b...[an,bnl 有如下性质 (1)bn-an=(b-a)/2m; (2)am1≥an,bH1≤bn; (3)f(am)f(bn)<0. 当n充分大时,令 Xn= bn+an 2 3/14
3/14 二分法计算过程中产生区间序列 [ak,bk] (k= 1,2,3,……) 显然有 [a,b] [a1,b1] [a2,b2] … [an,bn ] 有如下性质 (1)bn – an = (b – a)/ 2 n; (2)an+1 ≥ an,bn+1 ≤ bn ; (3)f(an)f(bn)< 0. 当n充分大时,令 2 n n n b a x

定理2.2设x*为方程f(x)=0在区间[a,b]内的唯一根, f(x)满足f(a)f(b)<0,则二分法计算过程中第n 个区间Ian,bml的中点xn满足不等式 k.-xlst -4 2+1 证:因为an≤x≤bn,所以 k.-x=2a,+6)-x=2a.-+w.-x sa.-x1+1,-x1 (x-a)+6.-x1 4/14
4/14 定理2.2 设x *为方程f(x)= 0在区间[a,b]内的唯一根, f(x)满足f(a)f(b)< 0,则二分法计算过程中第n 个区间[an,bn ]的中点xn满足不等式 1 * 2 n n b a x x 证:因为an≤ x * ≤ bn,所以 * * ( ) 2 1 x n x an bn x ( ) ( ) 2 1 * * an x bn x [| | | |] 2 1 * * a x b x n n [( ) ( )] 2 1 * * x a b x n n

故有 b-0= x.-xs b-a 2 2n+1 由此可知,当n→∞时,xm→x*,即二分法产生的序 列收敛。 5/14
5/14 1 * 2 2 n n n n b a b a x x 故有 由此可知,当n∞时,xn x * ,即二分法产生的序 列收敛

算法(二分法求解非线性方程) 第一步:输入误差限,81,计算y1←f(a),Jy2← f(b); 第二步:计算x,←0.5(+b),y←f(x),若 l =so, 则输出x,结束。否则转第三步; 第三步:若%y则转第二步;否则,输出x结 束。 6/14
6/14 算法(二分法求解非线性方程) 第一步:输入误差限0,1,计算 y1 f(a),y2 f(b); 第二步:计算x0 0.5(a+b),y0f(x0),若 | y0 |1则转第二步;否则,输出x0结 束

例1.水中浮球问题 有一半径r=10cm的球体,密度 p=0.638.球体浸入水中后,浸入水 中的深度d是多少? 根据阿基米德定律,物体排开水的质量就是水对物 体的浮力。 M= axr'p v=mr2-(r-x)'l 整理得:d3-3rd2+4r3p=0 7/14
7/14 r d .水中浮球问题 有一半径r =10 cm的球体,密度 =0.638.球体浸入水中后,浸入水 中的深度d 是多少? 根据阿基米德定律,物体排开水的质量就是水对物 体的浮力。 3 3 4 M r d V r r x dx 0 2 2 [ ( ) ] 整理得: d 3 – 3 r d 2 + 4 r 3 = 0
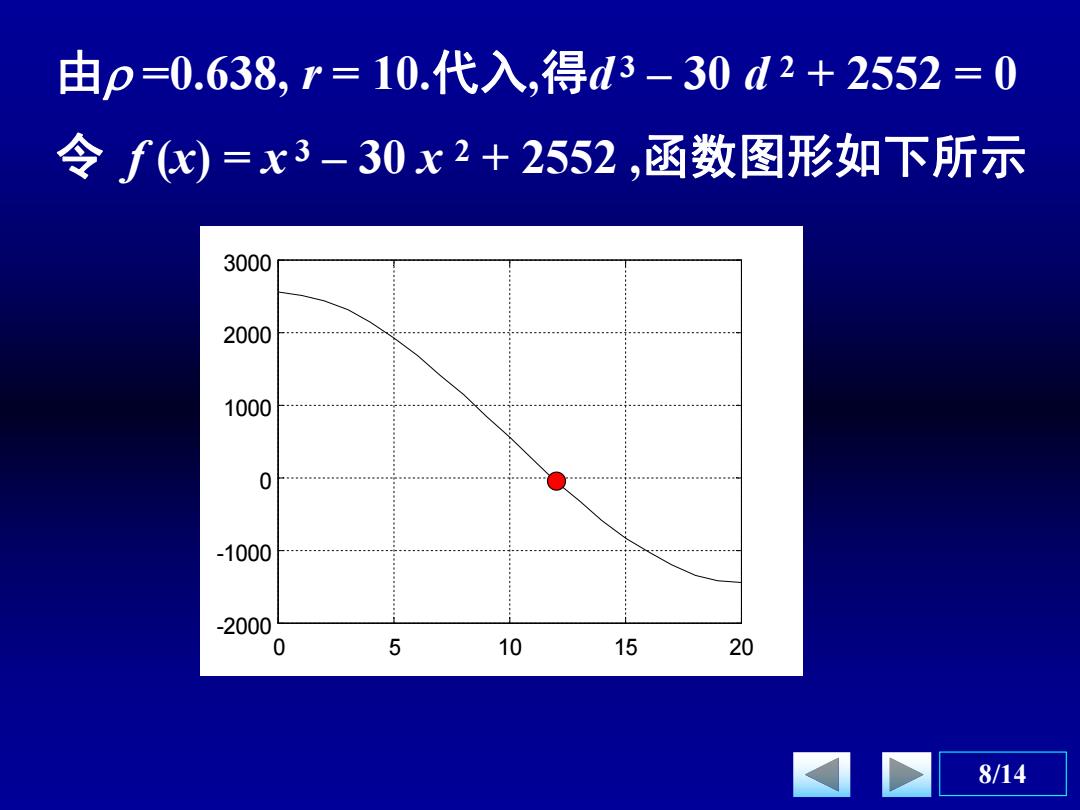
由p=0.638,r=10.代入,得d3-30d2+2552=0 令fx)=x3-30x2+2552,函数图形如下所示 3000 2000 1000 0 -1000 -2000 0 5 10 15 20 8/14
8/14 0 5 10 15 20 -2000 -1000 0 1000 2000 3000 由 =0.638, r = 10.代入,得d 3 – 30 d 2 + 2552 = 0 令 f (x) = x 3 – 30 x 2 + 2552 ,函数图形如下所示

水中浮球问题:x3-30x2+2552=0 delta =5e-6;eps 1e-6 def f(x): return x*x*x-30*x*x+2552 def MyBicection(f,a,b): n=1;fa=f(a);fb=f(b) while True: c=(a+b)/2; fc=f(c) print((三分次数 ,"0:.0f".format(n),"10:.4f".format(a),"0:.4f".format(a),"0:.4f".format(b)) n=n+1 if abs(fc)<delta: break elif fa*fc <0: b=c; fb=fc else: a=c; fa=fc if b-a<eps: break return c x=MyBicection(f,0,20) 11.861501 print(方程的根为x=',"{0:.6f".format(x)》 9/14
9/14 水中浮球问题: x 3 – 30 x 2 + 2552 = 0 x delta =5e-6;eps = 1e-6 def f(x): return x*x*x-30*x*x+2552 def MyBicection(f, a, b): n=1; fa= f(a); fb= f(b) while True: c=(a+b)/2; fc=f(c) print('二分次数 ' , "{0:.0f}".format(n), "{0:.4f}".format(a), "{0:.4f}".format(a), "{0:.4f}".format(b)) n=n+1 if abs(fc)<delta: break elif fa*fc <0: b=c; fb=fc else: a=c; fa=fc if b-a<eps: break return c x=MyBicection(f,0,20) print('方程的根为x=' , "{0:.6f}".format(x)) 11.861501
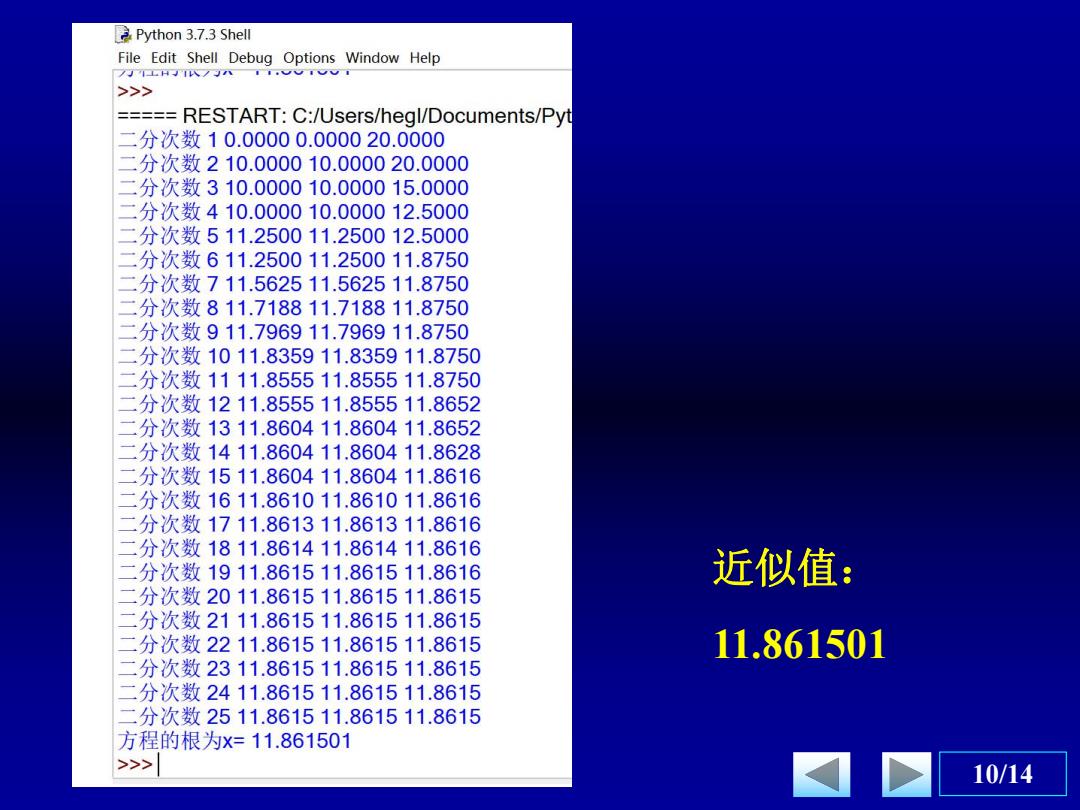
Python 3.7.3 Shell File Edit Shell Debug Options Window Help /JLHI八/八II心T >>> =====RESTART:C:/Users/hegl/Documents/Pyt 二分次数10.00000.000020.0000 二分次数210.000010.000020.0000 二分次数310.000010.000015.0000 二分次数410.000010.000012.5000 二分次数511.250011.250012.5000 二分次数611.250011.250011.8750 二分次数711.562511.562511.8750 二分次数811.718811.718811.8750 二分次数911.796911.796911.8750 二分次数1011.835911.835911.8750 二分次数1111.855511.855511.8750 二分次数1211.855511.855511.8652 二分次数1311.860411.860411.8652 二分次数1411.860411.860411.8628 二分次数1511.860411.860411.8616 二分次数1611.861011.861011.8616 二分次数1711.861311.861311.8616 二分次数1811.861411.861411.8616 二 分次数1911.861511.861511.8616 近似值: 二分次数2011.861511.861511.8615 二分次数2111.861511.861511.8615 分次数2211.861511.861511.8615 11.861501 二分次数2311.861511.861511.8615 分次数2411.861511.861511.8615 分次数2511.861511.861511.8615 方程的根为x=11.861501 >>> 10/14
10/14 近似值: 11.861501