电子科技大学：《数值分析 Numerical Analysis》课程教学资源（课件讲稿）收敛性分析初步

收敛性分析初步 向量序列的收敛性 迭代法的收敛性分析 迭代误差估计定理 平面温度场计算

1 向量序列的收敛性 迭代法的收敛性分析 迭代误差估计定理 平面温度场计算

平面点列： [网 lim 二 my0-g+-=0 X∈Rn:X),X2),…,X因，… lim X()=X*←→ liml(-"ll2=0 k→00 k→0 利用向量范数等价性，对任意范数‖·川 limX)=X*←〉 k→∞ m‖X-X=0 2

2 平面点列: ( ) * 1 1 ( ) * 2 2 lim k k k x x x x               lim ( ) ( ) 0 * 2 2 ( ) 2 * 2 1 ( ) 1      x x x x k k k X (k)∈Rn : X(1), X (2), ···, X (k) , ······· ( ) * lim X X k k   lim || ||2 0 ( ) *    X X k k ( ) * lim X X k k   lim || || 0 ( ) *    X X k k 利用向量范数等价性, 对任意范数 || · ||     (1) 2 (1) 1 x x     (2) 2 (2) 1 x x     ( ) 2 ( ) 1 k k x x ······ ······

AX=b(M-NX=bMX=NX+b 计算格式：X+I)=BX+f(B=M1N) 设方程组的精确解为X*,则有 X*=BX*+f X+)-X*=BX内-X*) 记8因=X-X*(k=0,1,2,3,·) 则有 E(k+1)=B e(k) k=B6k-1)（k=1,2,3, … 3

3 A X = b  (M–N )X = b  M X = N X + b 记  (k) = X(k) – X* ( k = 0, 1, 2, 3, ······ ) 则有  (k+1) = B  (k)  (k) = B  (k-1) ( k = 1, 2, 3, ······ ) 计算格式: X(k+1) = B X(k) + f ( B = M-1N ) X(k+1) – X*= B(X(k) – X*) 设方程组的精确解为 X* ,则有 X* = B X* + f 

E(k)=B &(k-1)=B2 &(k-2)=...=Bk (0) (1) limε=0 → lim B*0 k→00 k-→∞ j-- (2) m8)=0=B‖<1 lim[X(-"]=0 k-→00 lim X()=X k-→00 迭代格式Xk+1)=BX+f收敛 4

4 lim 0 lim 0 ( )      k k k B k (1)   (k) = B  (k-1)=B2  (k-2)=···=Bk  (0) lim [ ] 0 ( ) *    X X k k ( ) * lim X X k k   迭代格式 X(k+1) = B X(k) + f 收敛  (2)     lim 0 ( k ) k  B  1                     k k k                            k k k k k        1 1 1

命题若引B<1,则迭代法X+)=BX+f收敛 证：由8k)=Bk-1),得 lεkl≤Bεk-lW (k=1,2,3,…) →‖ε川≤‖Bk‖εol IBl<1→ msm‖B1s片0 所以 lim a()0 5

5 : 由 (k) = B  (k-1),得 ||  (k)|| ≤ || B|| ||  (k-1)|| ( k = 1, 2, 3, ······ ) lim 0 ( )   k k 所以  命题 若||B||<1,则迭代法 X(k+1) =B X(k) +f 收敛 ||  (k)|| ≤ || B||k ||  (0)|| lim || || lim || || || || 0 ( ) (0)       k k k k || B|| < 1 B  

注1：若 lim B=0 I 则 k-→o (I-B)1=I+B+B2+…十Bk+… 事实上 (I-B)(I+B+B2+…+Bk)=I-Bk+1 注2：X=BX-)+f=B(BXk-2)+)+f=… =BkX0)+（I+B++Bk-1)f ≈(I-B)1f 6

6 : 若 lim  0 则  k k B ( I - B) -1 = I + B + B2 + ······ + Bk + ······ 事实上 ( I - B)( I + B + B2 + ······ + Bk ) =I – Bk+1 : X(k) =B X(k-1) + f = B(B X(k-2) + f) + f =···· = Bk X(0) + ( I + B + ····+ Bk-1)f ≈ ( I – B ) -1 f

定义4.1A=(a)nx,如果 aa>∑1ag 则称A为严格对角占优阵. j≠i 例1常微分方程边值问题 -y”+y=x x∈(0,1) y(0)=0,Jy(1)=0. 求在x1=0.1,x2=0.2,…,xg=0.9处的数值解 -Jy-1+(2+h2)Jy-y*1=h2（F1,2,…,9) 2+h2 -1 xP -12+h2-1 -12+h2 yy」 7

7 A=(aij)n×n , 如果 则称A为严格对角占优阵.     n j i j aii aij 1 | | | |           (0) 0, (1) 0. (0,1) y y y y x x 常微分方程边值问题 求在 x1=0.1, x2=0.2, ···, x9=0.9 处的数值解 – yj-1 + (2 + h2) yj – yj+1 = xj h2 ( j= 1,2,···,9)                         2 9 2 2 2 1 9 2 1 2 2 2 1 2 1 2 1 2 1 x h x h x h y y y h h h     

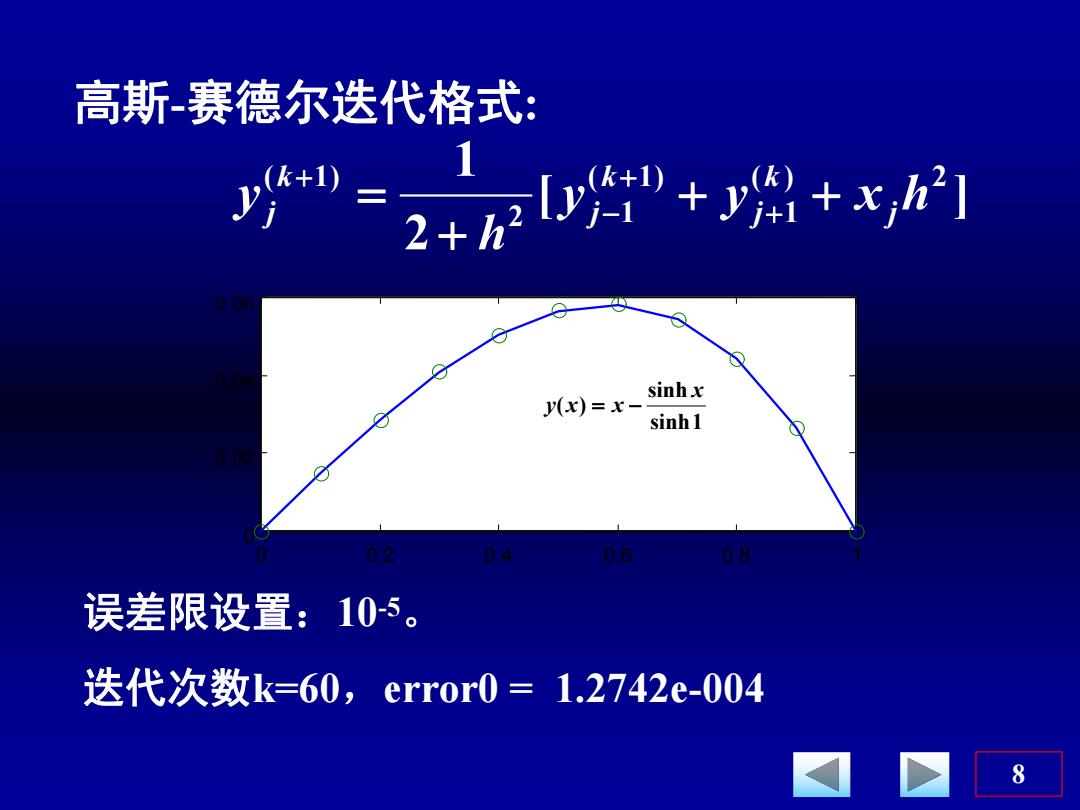
高斯-赛德尔迭代格式： "=2+京”+州+x =x- sinhx sinh1 02 04 06 6因 误差限设置：105。 迭代次数k=60,err0r0=1.2742e-004 8

8 高斯-赛德尔迭代格式: [ ] 2 1 ( ) 2 1 ( 1) 2 1 ( 1) y y x h h y j k j k j k j         0 0.2 0.4 0.6 0.8 1 0 0.02 0.04 0.06 误差限设置：10 -5 。 迭代次数k=60，error0 = 1.2742e-004 sinh1 sinh ( ) x y x  x 

定理4.3若Ax=b的系数矩阵A是严格对角占优 矩阵，则Jacobii迭代和Seideli迭代均收敛 证：由于矩阵A严格对角占优 Iaa>∑l j≠i i≠i 由A矩阵构造Jacobij迭代矩阵B,=D1(D-A) 第i行绝对值求和 =1 i≠i 所以 ∑1a,<1 9

9 若Ax=b的系数矩阵A是严格对角占优 矩阵,则Jacobi迭代和Seidel迭代均收敛 : 由于矩阵A严格对角占优 由A矩阵构造Jacobi迭代矩阵BJ = D-1(D – A) 第 i 行绝对值求和   n j i j ij ii a a 1 | | | | 1 所以 | |} 1 | | 1 || || max{ 1 1         n j i j ij ii i n J a a B | | 1 | | 1 1     n j i j ij ii a  a    n j i j aii aij 1 | | | | 

矩阵B的谱 设n阶方阵B的n个特征值为：入1，人2，…，九n 则称集合{21,22，…，九n} 为B的谱.记为chB 特征值取模最大 矩阵B的谱半径p(B)=max|2. 1<ksn 注1：当B是对称矩阵时，‖Bl2=pB) 注2：对Rn×n中的范数‖·，有 PB)≤I‖B‖ 10

10 矩阵B 的谱 设n阶方阵B 的n个特征值为:    n , , , 1 2  则称集合 { , , , } 1 2   n 为B 的谱. 记为 ch B 矩阵B的谱半径 ( ) max | | 1 k k n  B     注1: 当B是对称矩阵时, ||B||2 = (B) 注2: 对 Rn×n 中的范数|| · ||,有 (B) ≤ || B || 特征值取模最大