
迭代法的一般理论 >不动点迭代法 >不动点迭代的收敛性 >迭代序列的收敛速度 >序列收敛加速方法
1 迭代法的一般理论 Ø不动点迭代法 Ø不动点迭代的收敛性 Ø迭代序列的收敛速度 Ø序列收敛加速方法

>不动点迭代法 将一个计算过程反复进行称为迭代,迭代法是一类常 见常用的计算技术。 一种圆周率计算方案: =1- 11 4 3 初值:x=1 (-1)” 迭代格式: 七n=-1+ (n=1,2,3,…)) 2n+1 2
2 一种圆周率计算方案: 7 1 5 1 3 1 1 4 初值: x0=1 2 1 ( 1) 1 n x x n n n 迭代格式: ( n=1,2,3,······ ) 将一个计算过程反复进行称为迭代,迭代法是一类常 见常用的计算技术。 Ø不动点迭代法

>不动点迭代法 实验:在Pythont中反复计算x=math.sqrt(l+x) 实际是计算: x=v1+x 为方程:f(x)=x2-x-1的一个根: x= 2 w=--17x=1+x? x- 1+ 5 2 3
3 实际是计算: x 1 x 为方程: 2 1 5 x 实验:在Python中反复计算 Ø不动点迭代法 x math.sqrt(1 x) ( ) 1 2 f x x x 的一个根: ( ) 1 2 f x x x x 1 x 2 1 5 x
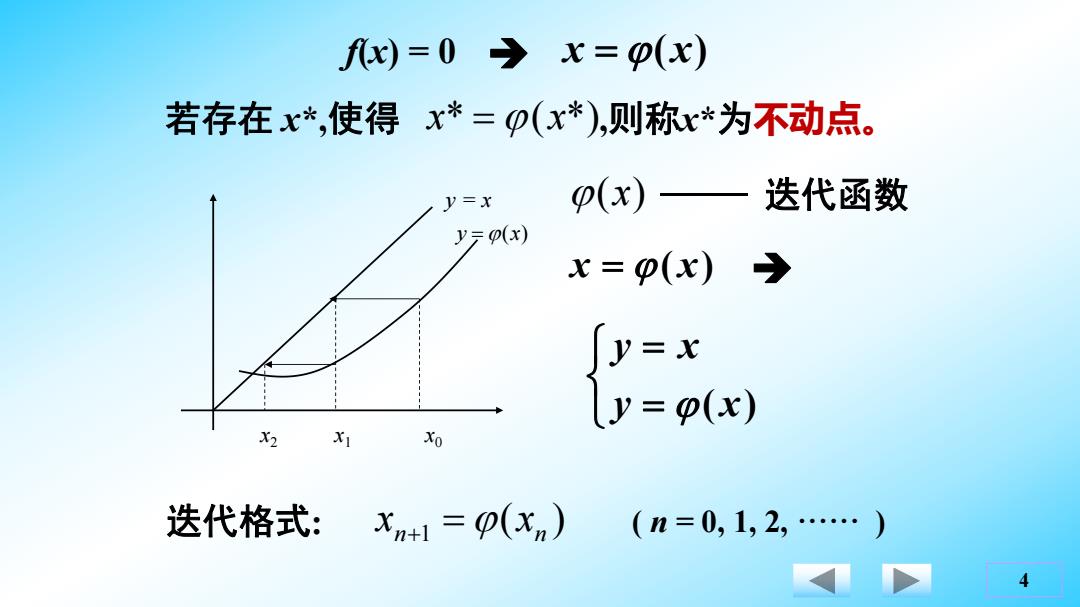
fx)=0→x=p(x) 若存在x*,使得x*=0(x*),则称x*为不动点。 y=x p(x)—迭代函数 p(x) x=p(x)→ Jy=x ly=o(x) X2 xo 迭代格式:Xn+1=p(xn) (n=0,1,2,… 4
4 x2 x1 x0 y = x y (x) f(x) = 0 x (x) (x) 迭代函数 若存在 x* ,使得 x* (x*),则称x*为不动点。 x ( x) y ( x) y x 迭代格式: ( ) n 1 n x x ( n = 0, 1, 2, ······ )

例2.1方程x3+4x2-10=0在[1,2】上有一个根,将方程变 换成另一形式: (1)x=√10-x3/2 p(x)=V10-x3/2 七H1=p(Xn) (n=0,1,2,…) ,=1.5 (2)x=V10/(x+4) p(x)=V10/(x+4) x=x) (n=0,1,2,…) =1.5 5
5 方程 x3 + 4x2 – 10 = 0 在 [1, 2] 上有一个根, 将方程变 换成另一形式: (1) 10 / 2 3 x x ( ) 10 / 2 3 x x 1.5 ( ) 0 1 x xn xn ( n = 0, 1, 2, ······) 1.5 ( ) 0 1 x xn xn ( n = 0, 1, 2, ······) (x) 10 /(x 4) (2) x 10 /(x 4)

import math def f(x): x3+4x2-10=0 return 0.5*math.sqrt(10-x*x*x) x0=1.5;er=1;k=0; X1,X2= while er>0.00001: -2.6826+0.3583i x=f(x0) -2.6826-0.3583i er=abs(x-x0) 1.3652 x0=x k=k+1 printe(迭代次数',"{0:.0f".format(k),'方 =16 程的根为x=',"{0:.6f".format(0) x=1.3652 6
6 import math def f(x): return 0.5*math.sqrt(10-x*x*x) x0=1.5; er=1; k=0; while er>0.00001: x=f(x0) er=abs(x-x0) x0=x k=k+1 print('迭代次数' , "{0:.0f}" .format(k), '方 程的根为x=' , "{0:.6f}" .format(x0)) x3 + 4x2 – 10 = 0 k=16 x0=1.3652 x1 ,x2 = -2.6826 + 0.3583i -2.6826 - 0.3583i 1.3652

import math def f(x): x3+4x2-10=0 return 0.5*math.sqrt(10/(4+x)) x0=1.5;er=1;k=0; X1,X2= while er>0.00001: -2.6826+0.3583i x=f(x0) -2.6826-0.3583i er=abs(x-x0) 1.3652 x0=x k=k+1 print('迭代次数',"{0:.0f".format(k),'方 k=6 程的根为x=,"{0:.6f".format(x0) x,=1.3652 7
7 x3 + 4x2 – 10 = 0 import math def f(x): return 0.5*math.sqrt(10/(4+x)) x0=1.5; er=1; k=0; while er>0.00001: x=f(x0) er=abs(x-x0) x0=x k=k+1 print('迭代次数' , "{0:.0f}" .format(k), '方 程的根为x=' , "{0:.6f}" .format(x0)) k=6 x0=1.3652 x1 ,x2 = -2.6826 + 0.3583i -2.6826 - 0.3583i 1.3652

>不动点迭代法需要研究的问题 ■构造有效的迭代格式 选取合适的迭代初值 ·对迭代格式进行收敛性分析 8
8 §构造有效的迭代格式 §选取合适的迭代初值 §对迭代格式进行收敛性分析 Ø不动点迭代法需要研究的问题
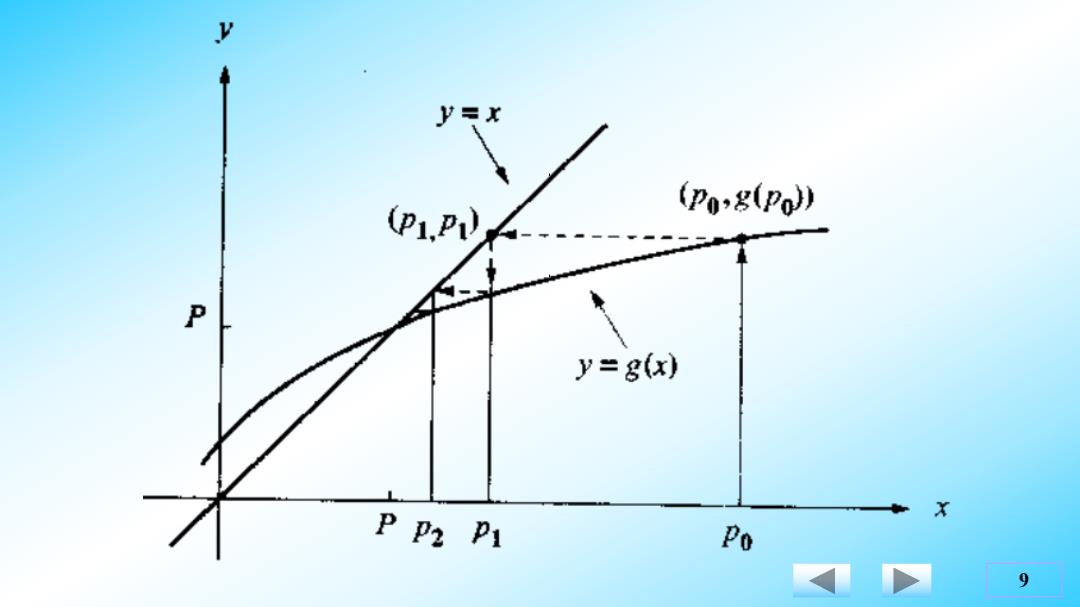
y=x P1,P) (Pog(Po)) P y=g(x) X PP吃P1 Po 9
9
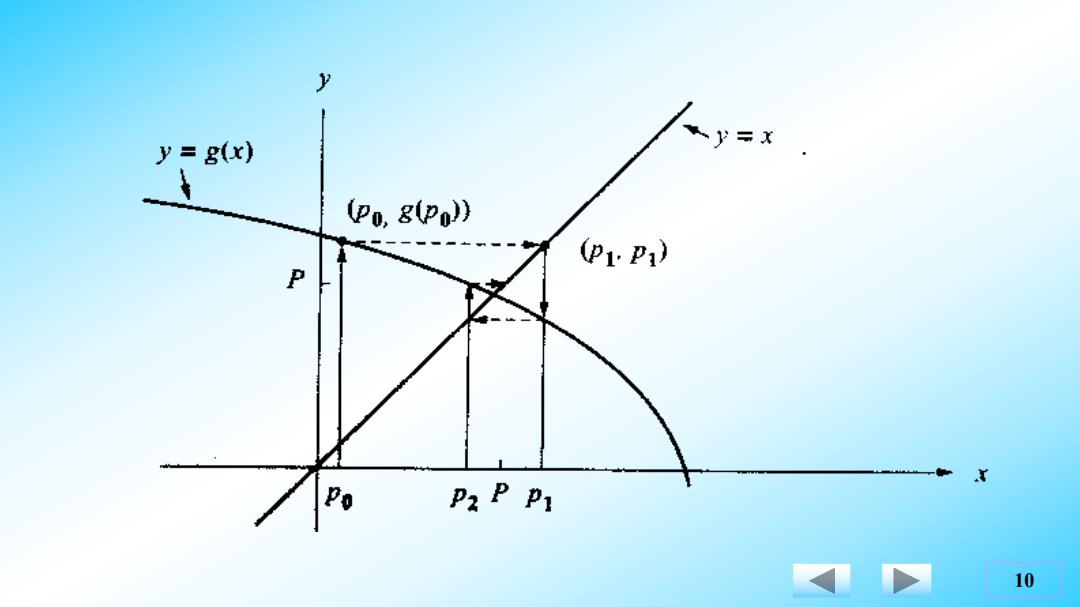
y=g(x) y =X (Po,g(P)) P1P1) P x Po P2 PP 10
10