电子科技大学：《数值分析 Numerical Analysis》课程教学资源（课件讲稿）向量和矩阵范数

3-3向量和矩阵范数 向量范数与矩阵范数 矩阵的条件数概念 Hilbert矩阵的条件数 1/19

1/19 向量范数与矩阵范数 矩阵的条件数概念 Hilbert矩阵的条件数 3-3 向量和矩阵范数

一 向量的范数 定义1设Rn是n维向量空间，如果对任意x∈Rn,都有 一个实数与之对应，且满足如下三个条件： (1)正定性：x20,且x=0 x=0; 2)齐次性：2x=x 入为任意实数 ③)三角不等式：x+≤x+y (y eRn) 则称x为向量x的范数 注：向量范数是向量长度概念的推广.例如 ∑x号=Vx+x2++x 是向量x的范数。 2/19

2/19 定义1 设 Rn是n维向量空间,如果对任意x∈Rn ,都有 一个实数与之对应,且满足如下三个条件: (1)正定性: ||x||≥0,且||x||=0 x = 0 ; (2)齐次性: x   x λ为任意实数 (3)三角不等式: ( y ∈Rn x  y  x  y ) 则称||x||为向量x的范数 . 注: 向量范数是向量长度概念的推广.例如 2 2 2 2 1 1 2 n n i  xi  x  x   x   是向量 x 的范数。 一、向量的范数

例1.设x=(1,x2,,xm)T∈Rn,则 )lx=∑1x,l 1-范数 i=1 2)Ix2=∑1x,P) 12-范数 (③)lx=|x,l 无穷范数 1<i<n 3/19

3/19 1 (3) i i n || x || max | x |     2 1 2 2 1 (2) ( ) n / i i || x || | x |    2 范数 无穷范数 1 1 (1) n i i || x || | x |    1范数 例1. 设 x=(x1 , x2 , ····, xn )T∈Rn，则

例2.证明x2是R上的一种范数 先证明柯西不等式：|xy上xh‖J2 对任意实数2，有（化-y)Tx-y)≥0→ 判别式 xx-22xy+23y乃y≥0 |xy12-(cx)0y乃y)≤0 今|xy≤xl2J2 4/19

4/19 例2. 证明 ||x||2 是 Rn 上的一种范数 先证明柯西不等式: | x Ty |≤ ||x||2·|| y||2 对任意实数λ, 有(x - λy)T(x - λy)≥0  x Tx – 2λx Ty + λ 2y Ty ≥0 | xTy |2 – (xTx)(y Ty) ≤0  | x Ty |≤ ||x||2·|| y||2 判别式

x+=(x+y)(x+y) =x"x+x"y+y"x+y"y ≤x+21xy+y ≤x+2川x2y2+y3 ‖x+y2≤x2+‖Jy2 (三角不等式成立) 1xh=Vx2+x,2++xn2≥0 (正定性成立) Ix-2=空21 (齐次性成立) 5/19

5/19 || || ( ) ( ) 2 2 x y x y x y T     x x x y y x y y T T T T     2 2 2 2 || x || 2 | x y | || y || T    2 2 2 2 2 2 || x || 2 || x || || y ||  || y || 2 2 2 || x  y || || x ||  || y || (三角不等式成立) || || 0 2 2 2 2 x 2 x1  x  xn  2 1 2 1 2 2 || x || ( x ) | | x | | || x || n i i n i i             (正定性成立) (齐次性成立)

正交变换下向量2-范数不变性 22=I,y=2x →y2=x2 y"y=(Qx)"(Qx)=x"Q"Qx =x"x llyIh=yyy=vx"x =lixlh 6/19

6/19 正交变换下向量2-范数不变性 QTQ= I , y =Qx y y Qx Qx x Q Qx x x T T T T T  ( ) ( )   2 2 || y || y y x x || x || T T      || y ||2 = || x ||2

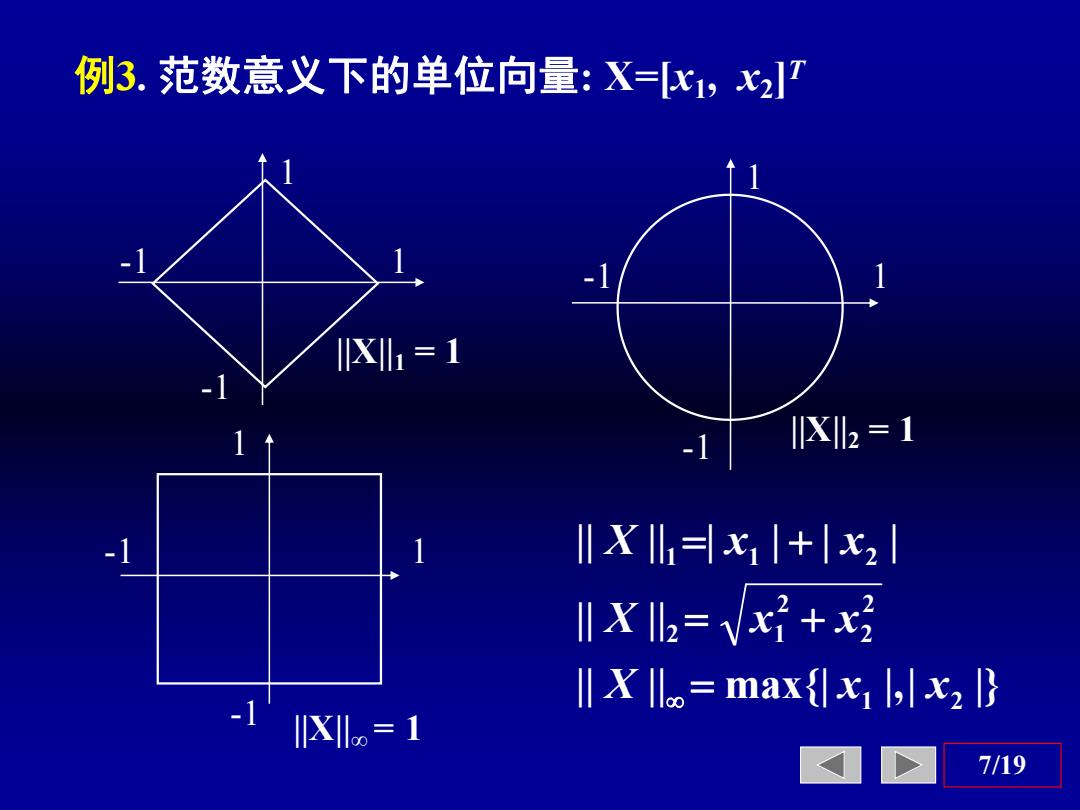
例3.范数意义下的单位向量：X=x1,x27 Xl1=1 -1 lX2 1 lXh=x,1+|x2 ll X I=v+ lXo=maxfx,,lx2} 1 XIldo 1 7/19

7/19 例3. 范数意义下的单位向量: X=[x1 , x2]T 1 -1 1 -1 ||X||2 = 1 -1 1 1 ||X||1 = 1 -1 1 -1 1 -1 ||X||∞ = 1 || || | | | | 1 1 2 X  x  x 2 2 2 2 1 || X ||  x  x || || max{| |,| |} 1 2 X  x x 

例4.设=（化1,2，…，x),证明 lll≤2 o 证明： lxl1=|x1|+|x2|+…+|xm1 max|≤n×max|xx| 1≤k≤n l≤k≤n 所以 lxo≤llxl1≤n‖xlo 8/19

8/19 例4. 设x=(x1 , x2 , ····, xn )T ,证明     || || || || || || 1 x x n x || || | | | | | | 1 1 2 n 证明 x  x  x    x : max | | || || max | | 1 1 1 k k n k k n x x n x            || || || || || || 1 所以 x x n x

定义2 设在Vm(P)上定义了Ixla,ll x两种向 量范数，若存在常数C1>0,C2>0,使得 C l≤lxlb≤C2 lVx∈Vn(P) 则称lxla与xlb等价. 定理1V(P)上的任意两个向量范数均等价 9/19

9/19 定义 2 设 在Vn (P)上定义了|| x ||a ,|| x ||b 两种向 量范数，若存在常数C1  0,C2  0，使得 1 2 || || || || || || ( ) C a b a n x  x  C x x V P 则称 || || 与|| || 等价. x a x b 定理 1 Vn (P)上的任意两个向量范数均等价

二、矩阵的范数 定义3设A∈Pmxm,若映射·‖：Pmxm→R 满足 (1)正定性‖A20,当且仅当A=0时，‖A=0; (2)齐次性|24曰2I川AI,V2∈R,VA∈Pmxm; (③)三角不等式川A+BIIIAI+|‖BVA,B∈Pm 则称映射‖|为pxm上的矩阵范数、 10/19

10/19 二、矩阵的范数 定义 3 A P P R 设  mn ，若映射 ||  ||： mn  满足 则称映射 || ||为 上的矩阵范数. m n p   (1)正定性 || A|| 0,当且仅当A  0时，|| A|| 0; (2) || || | ||| ||, , ; m n A A R A P  齐次性        (3) || || || || || ||, , . m n A B A B A B P  三角不等式     