电子科技大学：《数值分析 Numerical Analysis》课程教学资源（课件讲稿）拉格朗日插值与牛顿插值

拉格朗日插值与牛顿插值 代数插值基础介绍 拉格朗日插值公式 拉格朗日插值的误差分析 牛顿插值 三次Hermite插值

1 代数插值基础介绍 拉格朗日插值公式 拉格朗日插值的误差分析 牛顿插值 三次Hermite插值 拉格朗日插值与牛顿插值

0.6 插值法的应用背景 04 0.2 8 (1)复杂函数的计算； 6 (2)函数表中非表格点计算 4 3)光滑曲线的绘制； 68 (4)提高照片分辩率算法； 15 (⑤)定积分的离散化处理； 10 (6)微分方程的离散化处理 5 5 10 15 2

2 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 -0.4 -0.2 0 0.2 0.4 0.6 (1)复杂函数的计算; (2)函数表中非表格点计算 (3)光滑曲线的绘制; (4)提高照片分辩率算法; (5)定积分的离散化处理; (6)微分方程的离散化处理. 插值法的应用背景 5 10 15 5 10 15 2 4 6 8 2 4 6 8

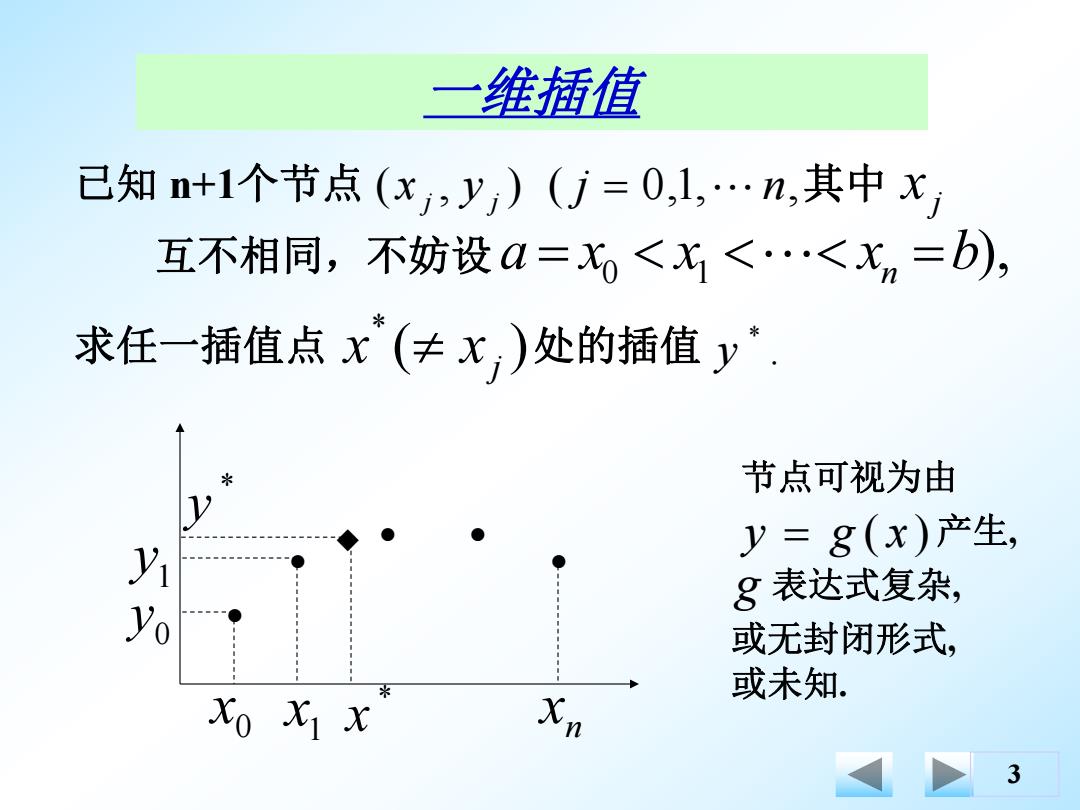
一维插值 己知n+1个节点(x),y)()=0,1,…n,其中Xj 互不相同，不妨设M=<X<…<xn=b), 求任一插值点x(≠x)处的插值y. 节点可视为由 y=8(x)产生， ● 8表达式复杂， 或无封闭形式， 或未知. XO X1 X 3

3 一维插值 已知 n+1个节点 ( x , y ) ( j 0,1, n, j j   其中 j x 互不相同，不妨设 ), a  x0  x1  xn b 求任一插值点 ( ) * j x  x 处的插值 . * y      0 x 1 x n x 0 y 1 y 节点可视为由 y  g ( x ) 产生, g 表达式复杂, 或无封闭形式, 或未知.  * x * y

插值问题基本提法： 寻求一个次数尽可能低的多项式p,满足条件： p(x)=yi (i=0,1,…,n). (1) 从几何上看，就是寻求一个最低次的多项式， 其几何曲线通过给定的n+1个点(x,y,),(i=0,1,…,n) 如果多项式p存在，则称p为f的插值多项式， xo,,…,xn称为插值节点（简称节点）， [a,b]称为插值区间， 条件(1)称为插值条件，f称为被插值函数

4

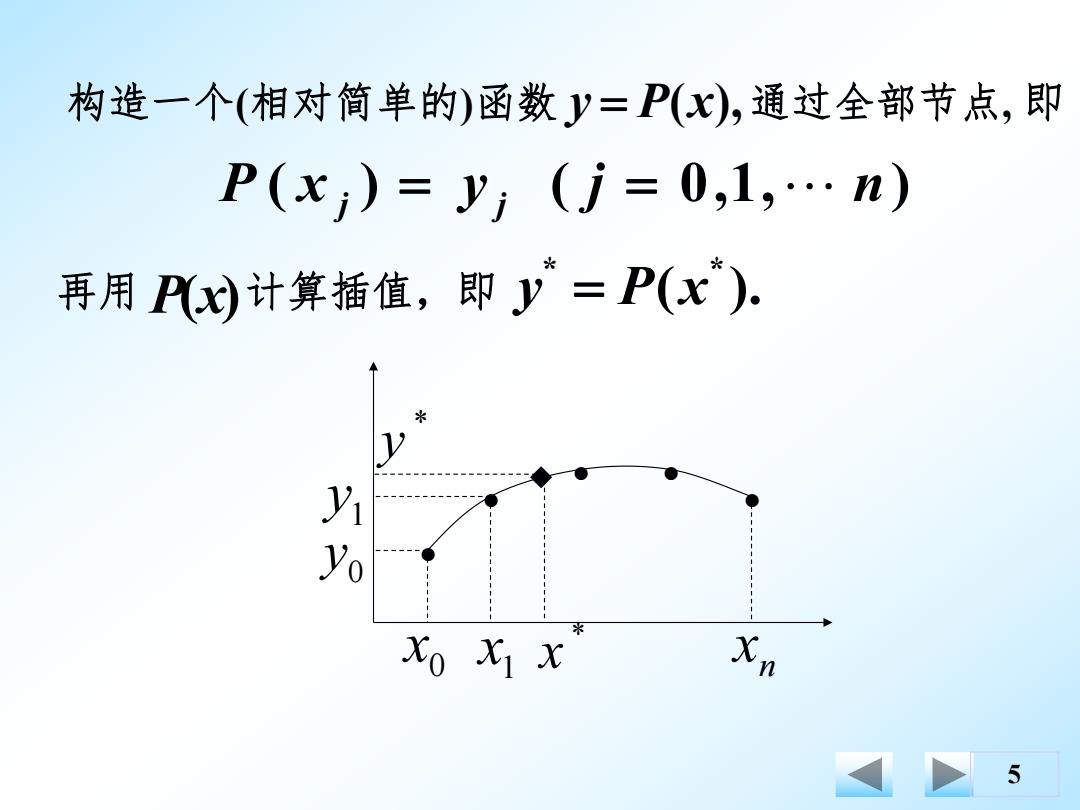
构造一个（相对简单的）函数y=P(x),通过全部节点，即 P(xi)=yi(j=0,1,…n) 再用Px计算插值，即y=P(X) 米 Xo XIx N 5

5 构造一个(相对简单的)函数 y  P(x),通过全部节点, 即 P ( x ) y ( j 0,1, n) j  j   再用 P(x)计算插值，即 ( ). * * y  P x      0 x 1 x n x 0 y 1 y  * x * y

定理1若插值结点x0,X1,,Xn是(+1)个互异 点，则满足插值条件Px)=yk(k=0,1,,n) 的n次插值多项式 P(x)a+ax......+anxm 存在而且是唯一的。 证明：由插值条件 P(xo)=Yo a+aXo+…+amX0=y0 P(x1)-y1 a0+411+…+an=y1 P(Xn)=yn +41Xn+…+nxi=yn 6

6 点,则满足插值条件 P(xk)= yk (k = 0,1,…,n) 的 n 次插值多项式 P(x)=a0 + a1x +……+ anxn 存在而且是唯一的。                  n n n n n n n n n a a x a x y a a x a x y a a x a x y     0 1 0 1 1 1 1 0 1 0 0 0 证明: 由插值条件 P(x0)= y0 P(x1)=y1 ··· P(xn )=yn 定理1 若插值结点x0 , x1 , ··· , xn 是 (n+1)个互异 

方程组系数矩阵取行列式 1 Xo xo 1 A= X1 三 Π(x;-xj)≠0 nzi>j20 1 Xn x 故方程组有唯一解。 从而插值多项式P(x)存在而且是唯一的. 7

7 n n n n n x x x x x x A     1 1 1 | | 1 1 0 0  方程组系数矩阵取行列式 故方程组有唯一解. 从而插值多项式 P(x) 存在而且是唯一的. ( ) 0 0        i j n i j x x

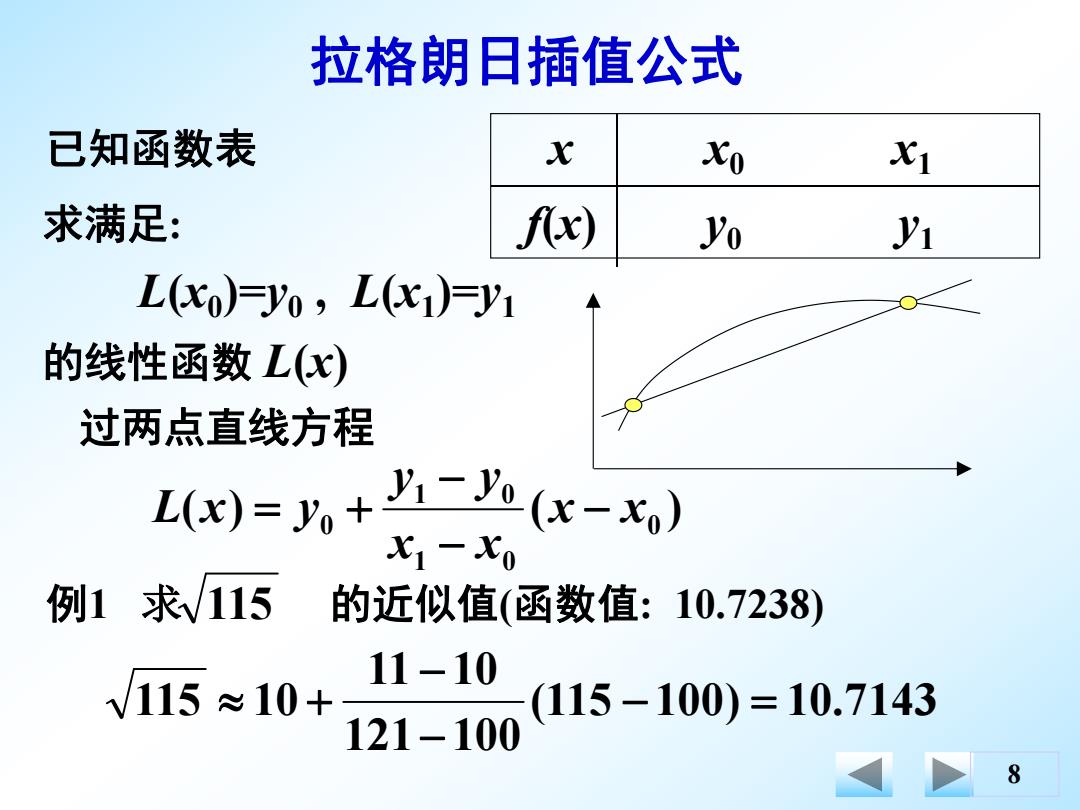
拉格朗日插值公式 已知函数表 x Xo x1 求满足： fx) Yo V1 L(xo)=yo,L(X1)y1 的线性函数L(x) 过两点直线方程 Lx)=+4-(x-x) X1-X0 例1求115 的近似值（函数值：10.7238） 11-10 W115≈10+ (115-100)=10.7143 121-100 8

8 ( ) ( ) 0 1 0 1 0 0 x x x x y y L x y      过两点直线方程 求满足: L(x0)=y0 , L(x1)=y1 的线性函数 L(x) 已知函数表 x x0 x1 f(x) y0 y1 例1 求 115 的近似值(函数值: 10.7238) (115 100) 10.7143 121 100 11 10 115 10       拉格朗日插值公式

L(9)=+4-4(c-x,) x1-X0 对称形式 L(x)= =片+- Yo 1-X0X1-X0 记 1,(g)==X,4()= -七 X1-X0 x1-xo 当x≤xsX1时 x Xo x1 0sI(x)≤1， L(x) 1 0 基函数 L(x) 0 1 0sI1(x)1 L(x)=1(x)yo+(x)y1 9

9 1 0 0 1 1 0 1 0 ( ) , ( ) x x x x l x x x x x l x      记  当 x0≤ x ≤x1 时 0≤l0(x)≤1, 0≤l1(x)≤1 x x0 x1 l0(x) 1 0 l1(x) 0 1 0 0 1 1 L(x)  l (x) y  l (x) y 0 1 0 1 1 1 0 0 ( ) y x x x x y x x x x L x      对称形式  ( ) ( ) 0 1 0 1 0 0 x x x x y y L x y      基函数

二次插值问题 已知函数表 x Xo xI X2 fx) Yo yI V2 求函数L(x)=40+41X+2x2满足： L()=y0,L(1)=y1,L(x2)=y2 L(x)=lo(x)Yo+l(x)v1+1(x)y2, 10

10 二次插值问题 x x0 x1 x2 f(x) y0 y1 y2 已知函数表 求函数 L(x)=a0 + a1x + a2 x2 满足: L(x0)=y0 , L(x1)=y1 , L(x2)=y2 L(x)=l0(x)y0+l1(x)y1+l2(x)y2