电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第五章 积分变换 5.2 Fourier变换应用（1/3）

激学物理方程与特殊函激精品课程 第五章积分变换 主讲：李明奇副教授

第五章 积分变换 主讲：李明奇 副教授

§5.2 Fourier?变换应用 AE里MA数 属A-TVCI 有AALL为框因 AND NONLINEARATA [4n-au=0,(-oo0) u(x,0)=p(x),u,(x,0)=y(x) Ou 现代数从超丛打17 =a20+fx,0.(-00 8t 偏微分方程的调和 u1=0=p(x) 分析方法 落长兴张波著 4,=a2uc,(x>0,t>0) u(x,0)=0 u(+o∞，t)=4.(+oo,t)=0,u,(0,t)=2,(Q为常数) 2 里件名系热

2 §5.2 Fourier变换应用   2 0, , 0 ( ,0) ( ), ( ,0) ( ) tt xx t u a u x t u x x u x x                 2 2 2 0 ( , ), , 0 ( ) t u u a f x t x t t x u x                       2 , 0, 0 ( ,0) 0 ( , ) ( , ) 0, (0, ) , t xx x x u a u x t u x u t u t u t Q Q               为常数

波动方程的定解问题 例求解无界弦振动方程的初值问题： un-a2ue=0,(-oo0) u(x,0)=p(x),u,(x,0)=Ψ(x) 解： 4,ne,D,uso)'io,i） dt2 [n(,0+2m2a(o,t0=0 dt2 i(w,0)=p(w),i(o,0)=中(o)

3 波动方程的定解问题 例 求解无界弦振动方程的初值问题:   2 0, , 0 ( ,0) ( ), ( ,0) ( ) tt xx t u a u x t u x x u x x               2 2 2 ˆ( , ), (j ) ( , ) ˆ tt xx d u t u u u t dt      2 2 2 2 ˆ( , ) ˆ( , ) 0 ˆ( ,0) ( ), ( ,0) ( ) ˆ ˆ ˆ t d u t a u t dt u u                   解：

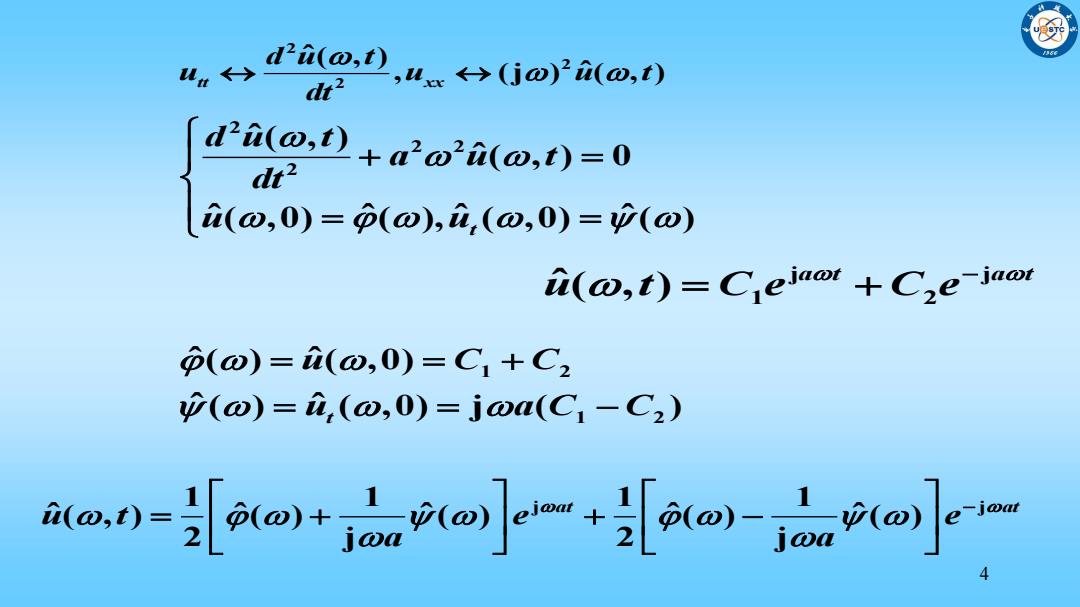
d2i(o, dt2 2,ux(jo)2(o,) Fi@Draoia(@t)-0 dr2 i(w,0)=p(ω)，i,(o,0)=中（ω） i(@,t)=Ceiao+C2e-iaor p(o)=(o,0)=C1+C2 p(w)=i,(o,0)=jw(C1-C2) ea-ow+dnuoj小e+aw,deoj]e

4 2 2 2 ˆ( , ), (j ) ( , ) ˆ tt xx d u t u u u t dt      2 2 2 2 ˆ( , ) ˆ( , ) 0 ˆ( ,0) ( ), ( ,0) ( ) ˆ ˆ ˆ t d u t a u t dt u u                   j j 1 2 ˆ( , ) a t a t u t C e C e       1 2 1 2 ˆ( ) ( ,0) ˆ ˆ( ) ( ,0) j ( ) ˆ t u C C u a C C              1 1 1 1 j j ˆ( , ) ( ) ( ) ( ) ( ) ˆ ˆ ˆ ˆ 2 j 2 j at at u t e e a a                              

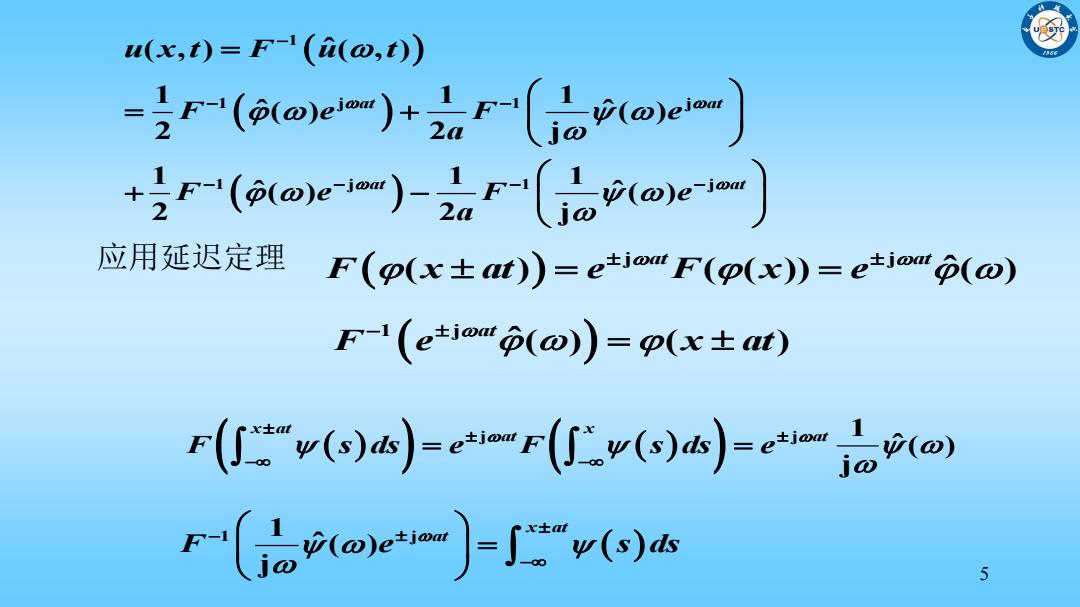
u(x,t)=F(i(@,t)) -r'(oe)+r(oe一) +=(eoem）--） 应用延迟定理 F(p(x±at)）=ekjouF(p(x)=etio" p() F-1(ejo"p(o)）=p(x±t) r()-v) F-（ooe」"(o)h 5

5       1 1 j 1 j 1 j 1 j ( , ) ( , ) ˆ 1 1 1 ˆ( ) ( ) ˆ 2 2 j 1 1 1 ˆ( ) ( ) ˆ 2 2 j at at at at u x t F u t F e F e a F e F e a                                        应用延迟定理   j j ( ) ( ( )) ( ) ˆ at at F x at e F x e              1 j ˆ( ) ( ) at F e x at                 j j 1 ˆ( ) j x at x at at F s ds e F s ds e                   1 j 1 ˆ( ) j x at at F e s ds                 

ax,)=[p(x+am)+(x-m】+2a[”w(s)k-∫w(sk] (x()ds 6Hz M 5Hz AAAAAU WMA

6     1 1 ( , ) ( ) ( ) 2 2 x at x at u x t x at x at s ds s ds a                             1 1 ( ) ( ) ( ) 2 2 x at x at x at x at s ds a           