电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第六章 Green函数法 6.3 基本解

§6.3基本解 偏微分方程的一种具有特定奇异性的解，由它可以构造出一般的解。 例如对于二维和三维拉普拉斯方程的基本解 W= u= 2En 4元CIMMo 阿达马，J.(-S.) J.(-S.)阿达马对二阶线性偏微分方程 44+2azy+az4y+b14.+b24,+c=0 在解析系数与非抛物(det(a0)的条件，得到以下基本解： u(M,M)=U(M,M)T"+V(M,M)Inr+W(M,M) 2

§6.3 基本解 2 偏微分方程的一种具有特定奇异性的解，由它可以构造出一般的解。 例如对于二维和三维拉普拉斯方程的基本解 0 4 MM q u  r  0 1 ln 2 MM q u  r  J. (-S.) 阿达马对二阶线性偏微分方程 11 12 22 1 2 2 0 xx xy yy x y a u a u a u b u b u cu       在解析系数与非抛物（det(αij)≠0）的条件，得到以下基本解: 0 0 0 0 ( , ) ( , ) ( , )ln ( , ) m u M M U M M V M M W M M      

一、L=0型方程的基本解 02+2 1.L=2 du ax dx a bi +c i,i=1 axi 2.L=6(M)的解，称为方程 Lu=f(M)的基本解 3.电量为一E。的点电荷的场满足△u=6(M) △u=f(M) 的基本解Ur)=-4元7 4.若U是一个基本解，是相应齐次方程的任一解u, Electric field 则U+u仍是基本解 Far field

3 一、Lu=0 型方程的基本解 4. 若U是一个基本解，是相应齐次方程的任一解u， 则U+u仍是基本解. 2 , 1 1 2 n n ij i i j i i j i L a b c   x x x           1. 3. 电量为  0 的点电荷的场满足   u M  ( ) 2. Lu M   ( ) 的解, 称为方程 Lu f M  ( ) 的基本解 1 ( ) 4 U r  r   u f M( ) 的基本解  

定理1Lu=f0的一个特解为 U*f=∬U(M-M,)fM,M, 证明： L4o*=L∬-M,aMm =J∬L(U(M-M,)f(M)aM, =S55(M-M.)f(M.)dM,=f(M) Note:UM*fM)=∬U(M-M,)fM,)M,仅为Lr)一个特解

4   3 0 0 0 ( ) R U f U M M f M dM     定理1 Lu=f(M)的一个特解为   3 3 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ) R R L U f L U M M f M dM L U M M f M dM                3 0 0 0 ( ) ( ) R     M M f M dM f M Note:   3 0 0 0 ( ) ( ) ( ) R U M f M U M M f M dM     仅为Lu=f(x)一个特解 证明:

二、热传导方程Cauchy问题的基本解 1定义： =L,(t>0,-o<x,y,z<+o) at u(x,y,z,0)=6(x,Jy,z) 的解Ucy,z,t),称为Cauchy问题 =Lu+f(x,y,,t) 8t u(x,v,,0)=(x,y,) 的基本解，也称为热传导方程Cauchy问题的Green函数 新江大学顾士学位论文 基本解方法求解各向异性热传导方程及其反阿题 基本解方法求解各向异性热传导方程及其反问题 摘要 在许多自然科学和工程技术领城不可湿免地要碰到偏微分方程反闲圆。鉴于各向异性材料 在实际应用中的重要性，本文考虑的是有关各向异性热传导方州的反问题

5 ,( 0, , , ) ( , , ,0) ( , , ) u Lu t x y z t u x y z x y z               ( , , , ) ( , , ,0) ( , , ) u Lu f x y z t t u x y z x y z           的解U(x,y,z,t)，称为Cauchy问题 的基本解 ,也称为热传导方程Cauchy问题的Green函数 1.定义： 二、热传导方程Cauchy问题的基本解

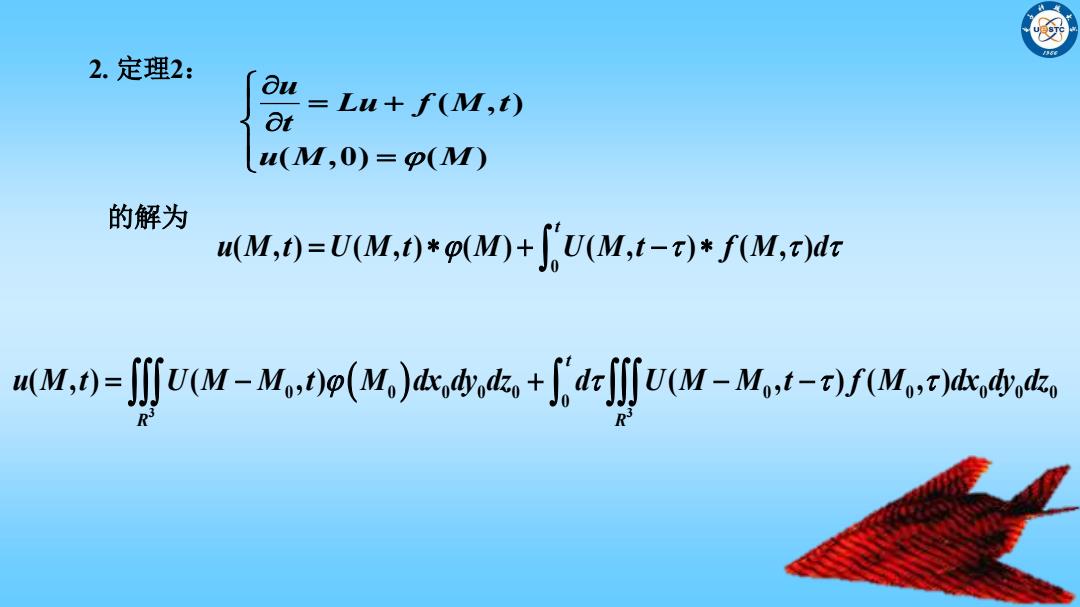
2.定理2： Ou 8t =Lu+f(M,t) u(M,0)=p(M) 的解为 u(M,t)=U(M,t)*o(M)+U(M,t-)*f(M,t)dz uM,=∬UM-M,0p(M,)dk,+dr∬UM-M,t-r)f(M.)d

6 2. 定理2： 0 ( , ) ( , ) ( ) ( , ) ( , ) t u M t U M t M U M t f M d             3 3 0 0 0 0 0 0 0 0 0 0 0 ( , ) ( , ) ( , ) ( , ) t R R u M t U M M t M dx dy dz d U M M t f M dx dy dz             的解为 ( , ) ( ,0) ( ) u Lu f M t t u M M          

例用Fourierz变换法求基本解 H,=a'Hs,-o0 u-o=p(x) 解： 即求 fy,=a2ye心 Vo=8(x) Fourier?变换 d应 dt --aoP 4 l,o=1 4国 4+国 4国 基本解：广=eao1 0w+ 253e+

7 例 用Fourier变换法求基本解 2 0 , , 0 ( ) t xx t u a u x t u x              解： 基本解 : 2 2 ˆ a t V e   2 0 ( ) t xx t V a V V x         即求 2 2 0 ˆ ˆ ˆ t 1 dV a V dt V           Fourier变换

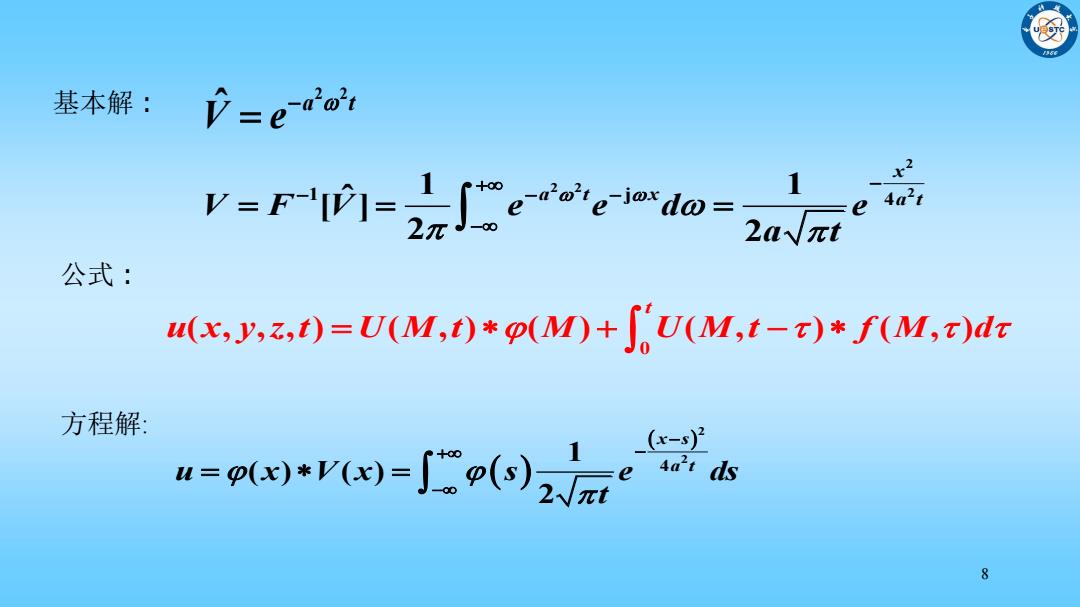
基本解：户=eaot r=r-II=2元J。era=a t? e4a2 aπt 公式： u(x,y,z,t)=U(M,t)*o(M)+[U(M,t-7)*f(M,t)dr 方程解： wr- 6

8 2 2 2 1 j 2 4 1 1 ˆ [ ] 2 2 x V F V e e d e a t x a t a t                   2 2 4 1 ( ) ( ) 2 x s a t u x V x s e ds t            方程解 : 基本解 : 2 2 ˆ a t V e   0 ( , , , ) ( , ) ( ) ( , ) ( , ) t u x y z t U M t M U M t f M d           公式 :