南京大学：《离散数学》课程教学资源（PPT课件讲稿）Lecture 17 布尔代数

1 布尔代数

布尔代数 1

回顾 2 口内容1：代数格的定义与性质 口满足结合律、交换律、吸收律，亦可通过此三性质定义 代数格 ▣内容2：格同态、格同构 口格同态具有保序性，格同构的充要条件 口内容3：分配格、有补格、有补分配格 口分配格满足分配率（两个判定定理），有界格存在全上界 和全下届，有补格所有元素存在补元，有补分配格即布 尔代数

 内容1：代数格的定义与性质  满足结合律、交换律、吸收律，亦可通过此三性质定义 代数格  内容2：格同态、格同构  格同态具有保序性，格同构的充要条件  内容3：分配格、有补格、有补分配格  分配格满足分配率(两个判定定理)，有界格存在全上界 和全下届，有补格所有元素存在补元，有补分配格即布 尔代数 2 回顾

本节提要 3 口内容1：布尔代数 口内容2：有限布尔代数表示定理

 内容1：布尔代数  内容2：有限布尔代数表示定理 3 本节提要

布尔代数的抽象定义 一个布尔代数是一个集合B,它有二元运算V和∧、 一元运算·以及特殊元素0和1，且B中元素满足下 列性质： 结合律 交换律 分配律 同一律 补律 (0,1,+,·,一，0,1)为布尔代数 口A的幂集构成一个布尔代数(p(A),U,∩，~，☑，A)

布尔代数的抽象定义  一个布尔代数是一个集合B，它有二元运算和、 一元运算 以及特殊元素0和1，且B中元素满足下 列性质：  ({0, 1}, +,  , , 0, 1)为布尔代数  A的幂集构成一个布尔代数((A), ⋃, ⋂,  , ,A） 4 结合律 交换律 分配律 同一律 补律

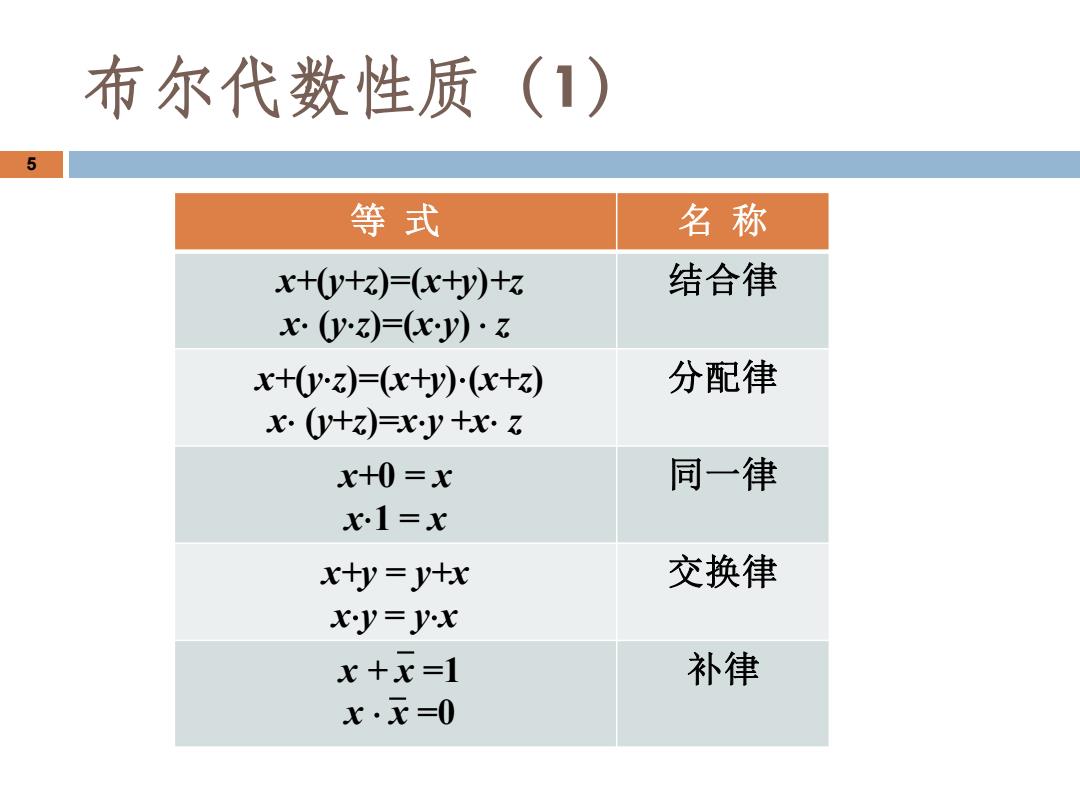
布尔代数性质(1) 5 等式 名称 x+0y+z)=(x+y)+z 结合律 x0yz=(xy)·z x+(y-z)=(x+y)(x+z) 分配律 x.(y)xy+x. x+0=x 同一律 x1=x x+y=y+x 交换律 xy=yx x+x=1 补律 x·x=0

等 式 名 称 x+(y+z)=(x+y)+z x (yz)=(xy)  z 结合律 x+(yz)=(x+y)(x+z) x (y+z)=xy +x z 分配律 x+0 = x x1 = x 同一律 x+y = y+x xy = yx 交换律 x + x =1 x  x =0 补律 5 布尔代数性质（1）

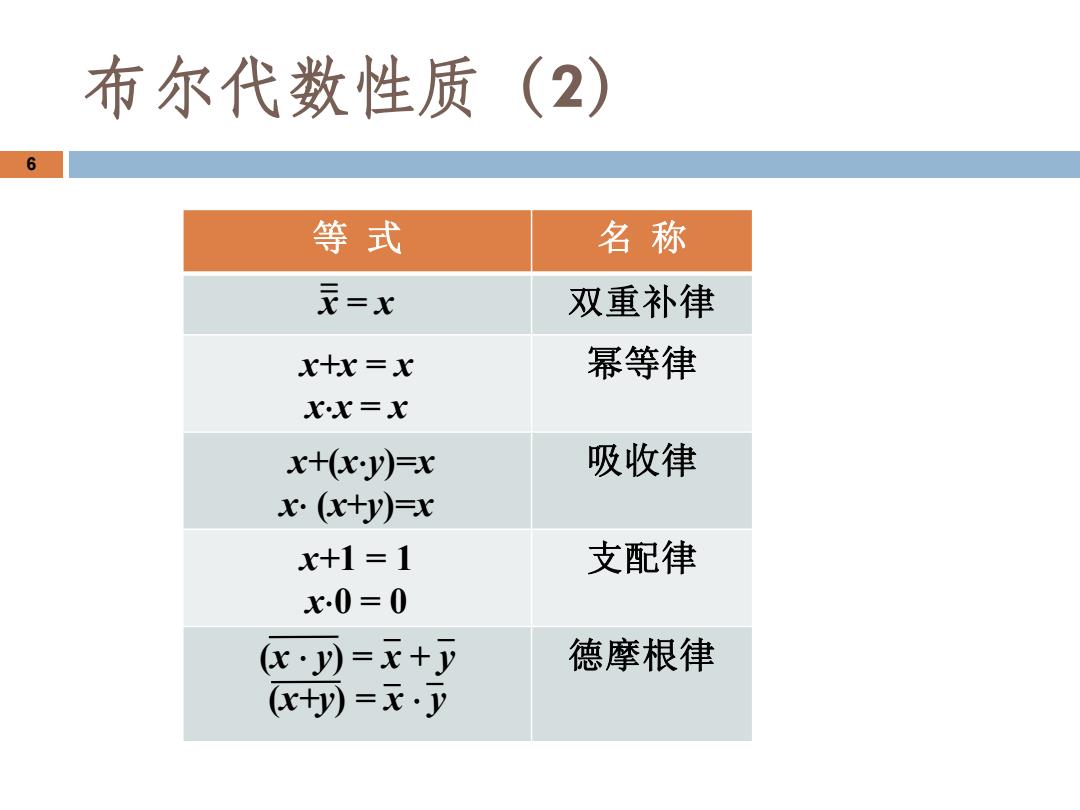
布尔代数性质(2) 6 等式 名称 元=x 双重补律 x+x=x 幂等律 xx=x x+(x.y)=x 吸收律 x.(x+y)=x x+1=1 支配律 x0=0 心y)=x+y 德摩根律 (x+y)=x.y

等 式 名 称 x = x 双重补律 x+x = x xx = x 幂等律 x+(xy)=x x (x+y)=x 吸收律 x+1 = 1 x0 = 0 支配律 (x  y) = x + y (x+y) = x  y 德摩根律 6 布尔代数性质（2）

布尔代数的性质证明 结合律、交换律、分配律、同一律、补律 口蕴含：支配律、吸收律、幂等律、双重补律、德摩根律 口证明支配律：x∈B,xv1=1,xA0=0 ▣xV1=1AcV1)=(rv)A(v1)=xV(依∧1)=xV=1 ▣x∧0=0V(xA0)=(KAV(KA0)=x∧（依V0)=xΛx=0

布尔代数的性质证明  结合律、交换律、分配律、同一律、补律 蕴含：支配律、吸收律、幂等律、双重补律、德摩根律  证明支配律：xB, x1=1, x0=0  x1= 1(x  1)= (x  x)(x 1)= x  (x  1)= x  x=1  x0= 0(x 0) =(x  x) (x 0)= x  (x  0)= x  x=0 7

布尔代数的性质证明 8 口证明吸收律 ▣xV(xy)=(xΛ1)V(Ky)=x∧(1Vy)=xA1=x 口x∧Vy)=(v0)Λ(xVy)=xV(0Ay)=V0=x 口证明幂等律 口x人=xA(xV0)=x(应用同一律、吸收律) 吸收律 幂等律 xAx=xA(xYxx)=x(两次应用吸收律)

 证明吸收律  x  (xy)= (x1)  (xy)= x  (1y) = x1 = x  x  (xy)= (x0)  (xy)= x  (0y) = x0 = x  证明幂等律  x  x= x  (x0) = x (应用同一律、吸收律） 吸收律 幂等律 x  x = x  ( x  (xx) ) = x (两次应用吸收律） 8 布尔代数的性质证明

布尔代数的性质证明 9 引理：x,y,z∈B,若xA=yAz且xVz=Vz,则x=y ▣x=xV(xAZ)=xv (AZ)=(cVy)A(cVz)∥吸收律/分配律 yy(A)=yv(xAZ)=Vx)) 口证明双重补律 axVx-l-EVx 口XAX=0=元Λ 口X=元

 引理：x, y, zB, 若 xz=yz 且 xz = yz ，则 x = y  x = x(xz) = x  (yz) = (x  y) (x  z ) //吸收律/分配律  y = y(y z ) = y  (xz) = (y  x) (y  z )  证明双重补律  x  x =1= x  x  x  x =0= x  x  x = x 9 布尔代数的性质证明

布尔代数的性质证明 10 0 证明德摩根律：Hx,yEB,cy)=xVy 口根据补元的唯一性，只需证明Vy是xAy的补元。 ()v(v)=(xvxv)A(vvxv)=1 (xA)A(xVJ)=(xAyA)v(y)=0

布尔代数的性质证明  证明德摩根律： x, yB, (xy)= x  y;  根据补元的唯一性，只需证明x  y是xy的补元。  (xy)(x  y)= (x  x  y )(y  x  y ) =1  (xy) (x  y)= (x  y x ) (x  y  y ) =0 10