
1 最短通路问题
最短通路问题 1

上节回顾 口内容1:欧拉图 口什么是欧拉图:含有欧拉回路 口欧拉图的充要条件:所有顶点度数为偶数 口如何构造欧拉回路:Fleuty算法 口内容2:哈密尔顿图 口什么是汉密尔顿图:含有汉密尔顿回路 ▣哈密尔顿图的必要和充分条件: ■必要条件:P(G-S)≤S,只能用来判断一个图不是汉密尔顿图 ■充分条件:Ore定理,只能用来判断一个图是汉密尔顿图 口哈密尔顿图有哪些应用
内容1:欧拉图 什么是欧拉图:含有欧拉回路 欧拉图的充要条件:所有顶点度数为偶数 如何构造欧拉回路:Fleury算法 内容2:哈密尔顿图 什么是汉密尔顿图:含有汉密尔顿回路 哈密尔顿图的必要和充分条件: ◼ 必要条件:P(G-S) |S|,只能用来判断一个图不是汉密尔顿图 ◼ 充分条件:Ore定理,只能用来判断一个图是汉密尔顿图 哈密尔顿图有哪些应用 上节回顾

本节提要 ▣内容1:Dijkstra算法 口内容2:Floyd-Warshall:算法 ▣内容3:旅行商问题(TSP) ▣内容4:最大流问题
内容1:Dijkstra算法 内容2:Floyd-Warshall算法 内容3:旅行商问题(TSP) 内容4:最大流问题* 本节提要

Dijkstra算法 4 Named after its inventor Edsger Dijkstra (1930-2002) Truly one of the "founders"of computer science This is just one of his many contributions
Dijkstra算法 4 Named after its inventor Edsger Dijkstra (1930-2002) Truly one of the "founders" of computer science This is just one of his many contributions

带权图与最短通路问题 口带权图:三元组(V,E,,(V,E是图,W是从E到 非负实数集的一个函数。W(e)表示边e的权。 口一条通路上所有边的权的和称为该通路的长度。 两点之间长度最小的通路称为两点之间的最短通路, 不一定是唯一的。 口单源点最短路问题 给定带权图G(V,E,)并指定一个源点,确定该源 点到图中其它任一顶点的最短路径
带权图:三元组 (V, E, W),(V, E)是图,W是从E到 非负实数集的一个函数。W(e)表示边e的权。 一条通路上所有边的权的和称为该通路的长度。 两点之间长度最小的通路称为两点之间的最短通路, 不一定是唯一的。 单源点最短路问题 给定带权图 G(V, E, W)并指定一个源点,确定该源 点到图中其它任一顶点的最短路径。 带权图与最短通路问题

Dijkstra算法的思想 口源点s到顶点v的最短路径若为S.uY,则s.u是s到u的最短路 径 口反之,可由近及远的计算s到所有点的最短路径 (-1)条最短路径按照由近及远(长度的非减次序)求得,设它们 的相应端点分别为u1,u1,最短路径长度记为d(s,),=1,…n- 1 每一步骤:选择最近的未知点并加入到已知点集合,更新$ 到其他未知点的距离 ▣假设前i条最短路径已知,第(+1)条最短路径长度: d(s,ui+1)=minfd(s,u)+W(ui,ui+)|j=1,...i)
源点s到顶点v的最短路径若为s…uv, 则s…u是s到u的最短路 径 反之,可由近及远的计算s到所有点的最短路径 (n-1)条最短路径按照由近及远(长度的非减次序)求得,设它们 的相应端点分别为u1 , …un-1,最短路径长度记为d(s, ui ) , i=1,…n- 1 每一步骤:选择最近的未知点并加入到已知点集合,更新s 到其他未知点的距离 假设前i条最短路径已知,第(i+1)条最短路径长度: d(s, ui+1 )=min{d(s, uj ) +W(uj , ui+1 )| j=1,…i} Dijkstra算法的思想

Dijkstra算法的描述 输入:连通带权图G,IVG=n,指定源顶点s∈Vc 输出:每个顶点v的标注(L(y),),其中: 口L(y)即从s到v的最短路径长度(目前可得的) 口u是该路径上v前一个顶点。 1.初始化:=0,S={s},L()=0,对其它一切eVG,将L()置为0。 若n=1,结束。 2.HeS=Vc-S,比较L()和L(+W4,)的值(4∈S) 如果L(+,)<L(),则将的标注更新为L(+马,,), 即:L()=min{L(),min{L(回+Wu)}} 3.对所有S中的顶点,找出具有最小L()的顶点口,作为41 4.S=SU{u41} 5.i=i+1;若i=n-1,终止。否则:转到第2步
输入:连通带权图G,|VG |=n, 指定源顶点sVG 输出:每个顶点v的标注(L(v), u), 其中: L(v)即从s到v的最短路径长度(目前可得的) u是该路径上v前一个顶点。 1.初始化:i=0, S={s}, L(s)=0, 对其它一切vVG , 将L(v) 置为。 若n=1,结束。 2.vS '=VG -S, 比较L(v)和L(ui )+W(ui , v)的值 (uiS) 如果L(ui )+W(ui , v)<L(v), 则将v的标注更新为(L(ui )+W(ui , v), ui ), 即: L(v)=min{ L(v), minuSi{L(u)+W(u,v)} } 3. 对所有S '中的顶点,找出具有最小L(v)的顶点v, 作为ui+1 4.S = S ⋃{ui+1} 5. i = i+1; 若i=n-1, 终止。否则:转到第2步。 Dijkstra算法的描述
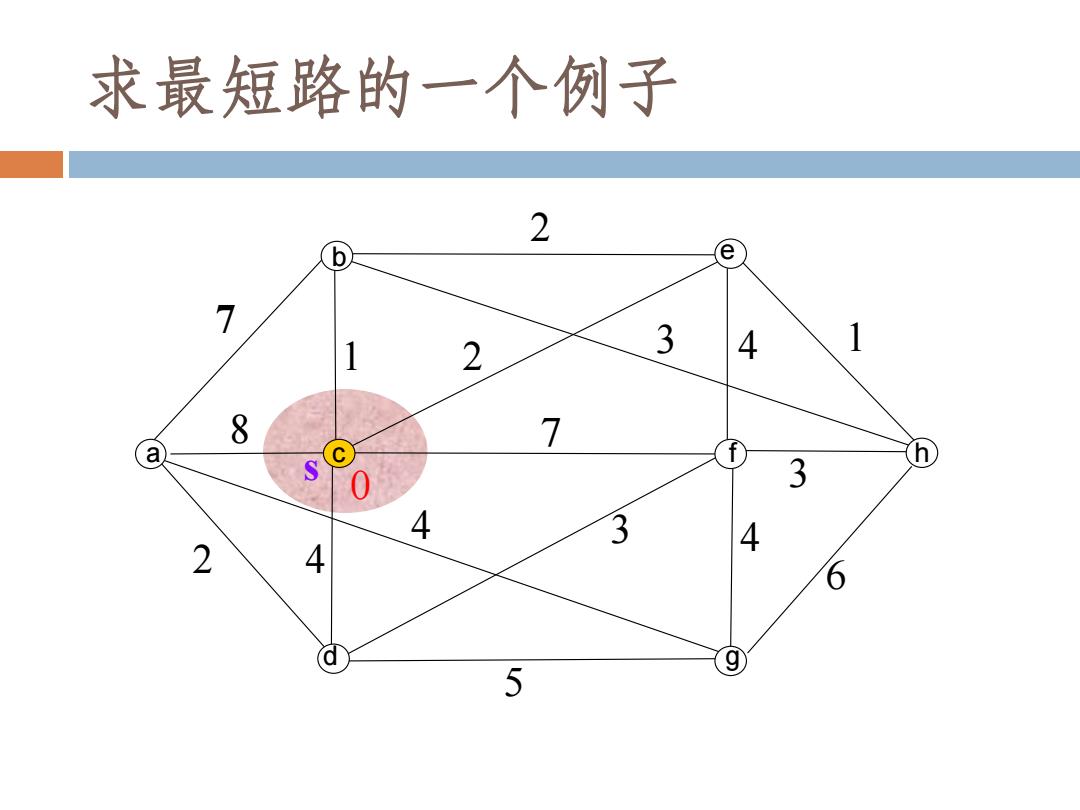
求最短路的一个例子 2 b e 7 1 2 3 4 1 8 7 a h 3 4 3 4 2 4 6 a 9 5
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 b a c d e f g h 求最短路的一个例子
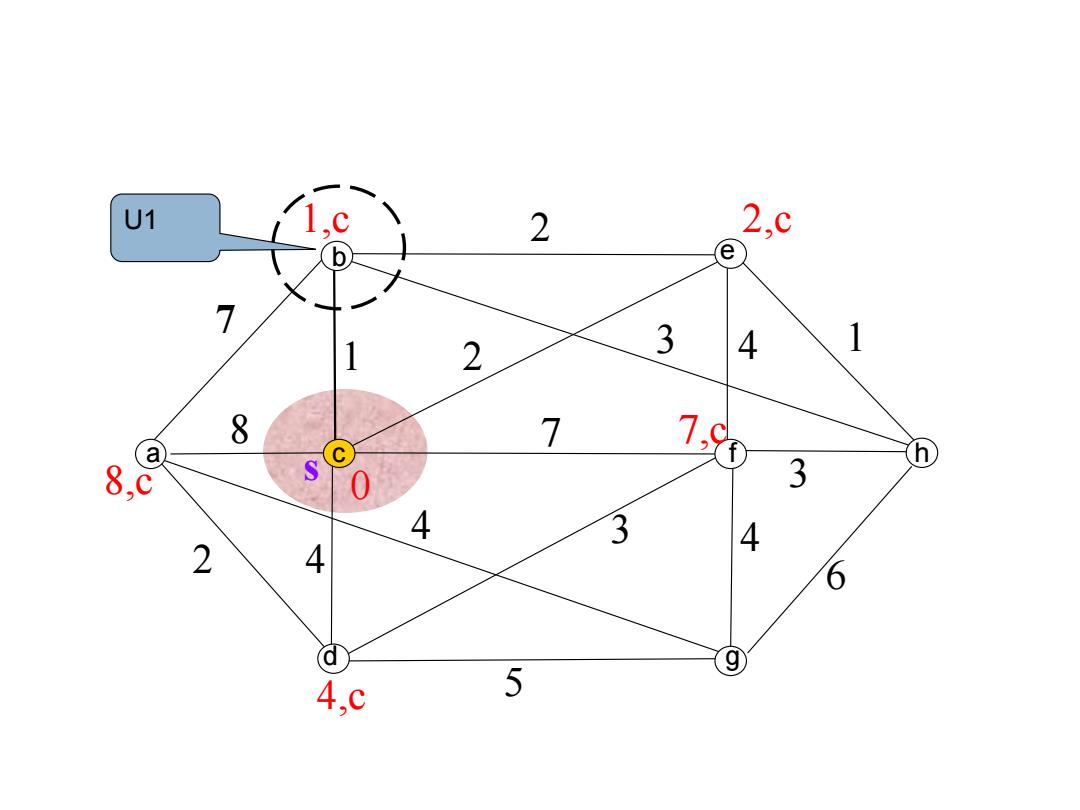
U1 2 2,c 7 1 2 3 4 1 8 7 18 h 8,c 3 4 3 4 2 4 6 d 9 4,C 5
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 7,c 4,c U1 b a cd efg h
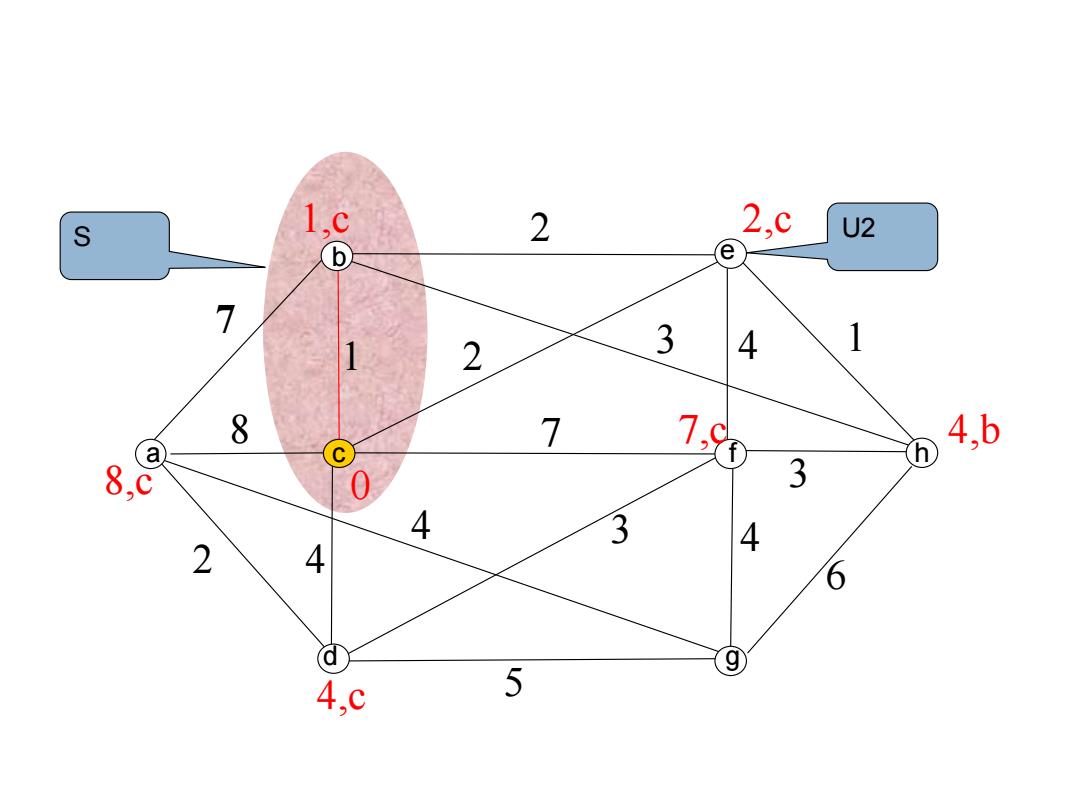
S 2 2,c U2 e 7 1 2 3 4 1 8 7 1 4,b h 8,c 3 4 3 4 2 4 6 a 9 4,C 5
7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 7,c 4,c U2 b a cd efg h 4,b S