
Advanced Algorithms Rounding Linear Program 尹一通Nanjing University,2022Fall
尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms Rounding Linear Program

Vertex Cover
Vertex Cover
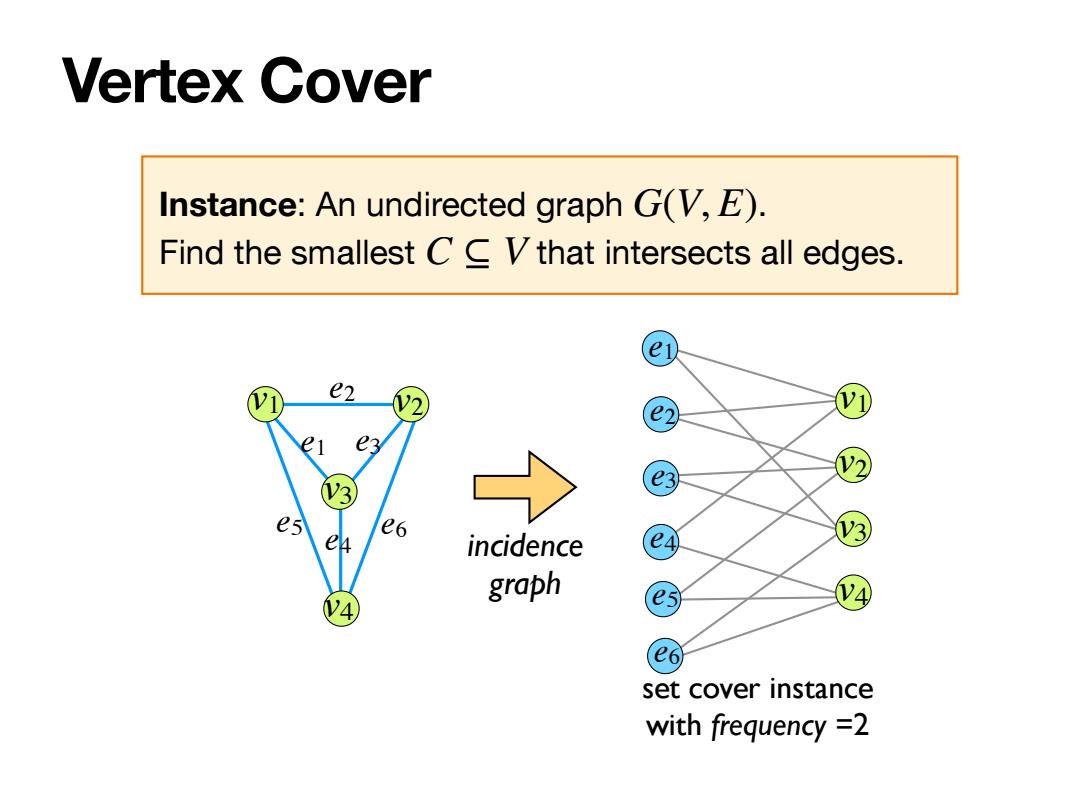
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. e2 e es e6 incidence graph V4 V4 set cover instance with frequency =2
Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V v1 v2 v3 v4 e1 e3 e2 e4 e1 e2 e3 e4 v1 v2 v3 e5 v4 e6 incidence graph set cover instance with frequency =2 e5 e6

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. ·NP-hard In(n)-approximation by greedy set cover 2-approximation algorithm: Find a maximal matching; return the matched vertices; .[Khot,Regev 2008]Assuming the unique games conjecture, there is no poly-time(2-e)-approximation algorithm
• NP-hard • -approximation by greedy set cover • 2-approximation algorithm: • [Khot, Regev 2008] Assuming the unique games conjecture, there is no poly-time -approximation algorithm. ln(n) (2 − ϵ) Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V Find a maximal matching; return the matched vertices;
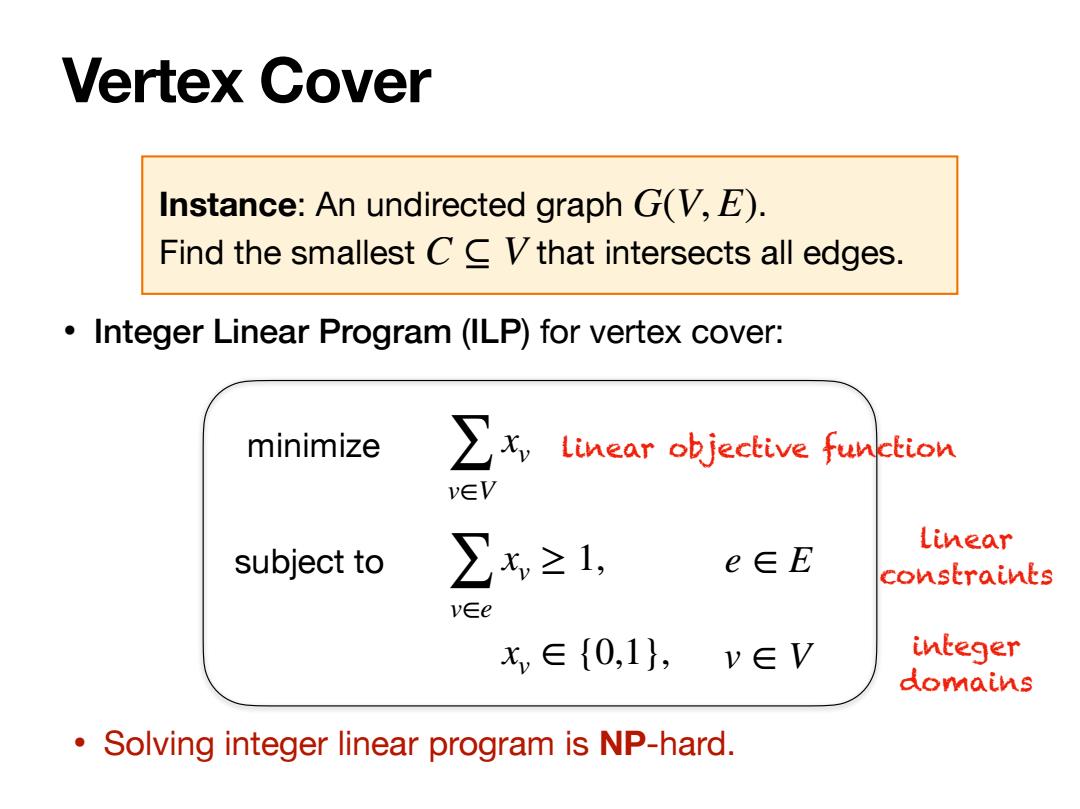
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest CC Vthat intersects all edges. Integer Linear Program(ILP)for vertex cover: minimize ∑x linear objective function v∈V subject to ∑x≥1, Linear e∈E constraints v∈e x,∈{0,1},v∈V integer domains Solving integer linear program is NP-hard
• Integer Linear Program (ILP) for vertex cover: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V linear objective function linear constraints integer domains • Solving integer linear program is NP-hard

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C Vthat intersects all edges. Linear Program(LP)relaxation: minimize ∑x v∈V subject to ∑x≥1, e∈E v∈e x∈[0,1], v∈V fractional domains linear programs are solvable in polynomial time!
• Linear Program (LP) relaxation: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V • linear programs are solvable in polynomial time! [ ] fractional domains

Linear Programming (LP) ·General form: matrix A={dijmxin],sets M [ml and NS [n] minimize cTx subject to afx =bi i∈M a,x≥b i∈M 光≥0 j∈N x;unconstrained j∈N
• General form: • matrix A = {a , sets and ij }[m]×[n] M ⊆ [m] N ⊆ [n] Linear Programming (LP) minimize subject to cTx aT i x = bi aT i x ≥ bi xj ≥ 0 xj unconstrained i ∈ M i ∈ M j ∈ N j ∈ N

Linear Programming (LP) General form: Canonical form: min cTx s.t. ajx=b i∈M min cTx ax≥b, i∈M → s.t.Ax≥b 为≥0 j∈N x≥0 x;unconstrained j∈N -6-{的0 x;unconstrained→ 5咖e0 (七≥0
Linear Programming (LP) min s.t. cTx aT i x = bi aT i x ≥ bi xj ≥ 0 xj unconstrained i ∈ M i ∈ M j ∈ N j ∈ N General form: Canonical form: aT i x = bi ⟹ { aT i x ≥ bi −aT i x ≥ − bi x where j unconstrained ⟹ xj = x+ j − x− j { x+ j ≥ 0 x− j ≥ 0 ⟹ min s.t. cTx Ax ≥ b x ≥ 0

Convex Polytopes 。hyperplane: subspace of dimension n-1 ∑a45=b j=1 (closed,affine)halfspace: ∑a4y≥b j=1 。convex polyhedron: intersection of finitely many halfspaces convex polytope:bounded convex polyhedron
• hyperplane: subspace of dimension • (closed, affine) halfspace: • convex polyhedron: intersection of finitely many halfspaces • convex polytope: bounded convex polyhedron n − 1 n ∑ j=1 ajxj = b n ∑ j=1 ajxj ≥ b Convex Polytopes

Integrality min cTx s.t.Ax≥b Z LP-relaxation
x ∈ ℤn Integrality min s.t. cTx Ax ≥ b LP-relaxation