
本次课主要内容 (一)、树的概念与应用 (二)、树的性质 (三)、树的中心与形心
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、树的概念与应用 (二)、树的性质 (三)、树的中心与形心
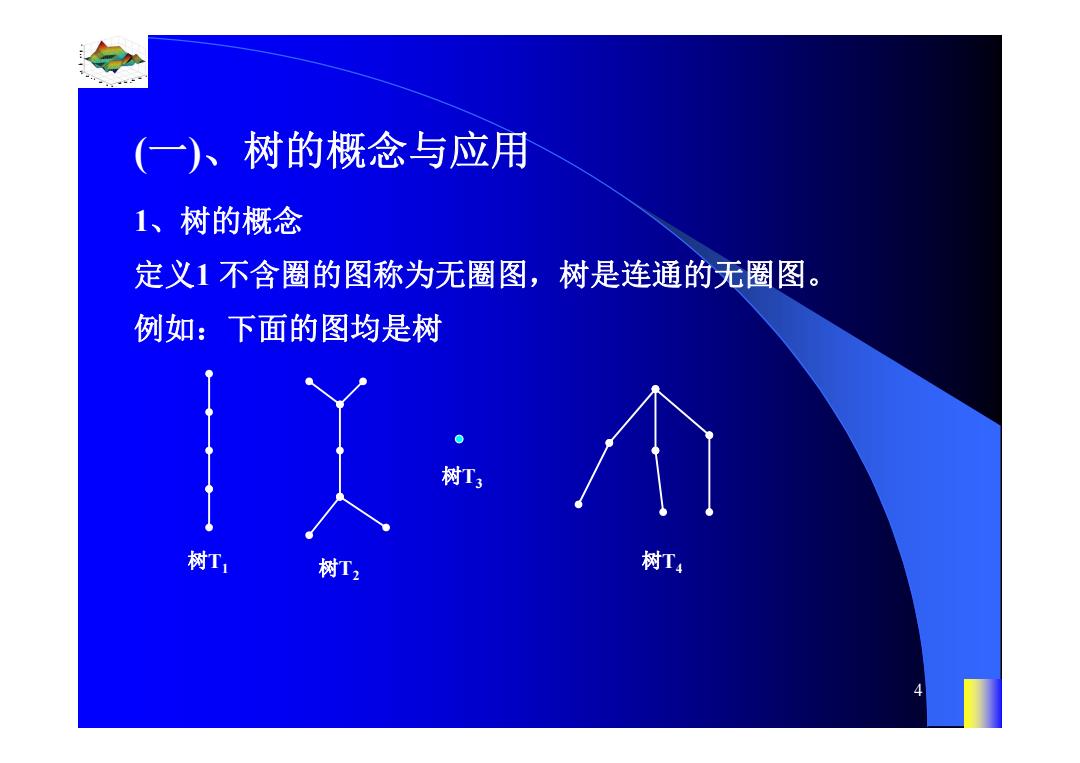
(一)、树的概念与应用 1、树的概念 定义1不含圈的图称为无圈图,树是连通的无圈图。 例如:下面的图均是树 树T3 树T, 树T2 树T4
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 1、树的概念 (一)、树的概念与应用 定义1 不含圈的图称为无圈图,树是连通的无圈图。 例如:下面的图均是树 树T1 树T2 树T3 树T4

定义2称无圈图G为森林。 注:(1)树与森林都是单图; (2)树与森林都是偶图。 例1画出所有不同构的6阶树。 解:按树中存在的最长路进行枚举。6阶树中能够存在 的最长路最小值为2,最大值为5。 火义平
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定义2 称无圈图G为森林。 注: (1)树与森林都是单图; (2) 树与森林都是偶图。 例1 画出所有不同构的6阶树。 解:按树中存在的最长路进行枚举。6阶树中能够存在 的最长路最小值为2,最大值为5

2、树的应用 树是图论中应用最为广泛的一类图。在理论上,由 于树的简单结构,常常是图论理论研究的“试验田” 在实际问题中,许多实际问题的图论模型就是树。 例2族谱图与树 要把一个家族的繁衍情况简洁直观表达出来,用点 表示家族中成员,成员x是成员y的儿女,把点x画在点 y的下方,并连线。如此得到的图,是一颗树,称为根 树。示意如下: 根树
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 树是图论中应用最为广泛的一类图。在理论上,由 于树的简单结构,常常是图论理论研究的“试验田”。 在实际问题中,许多实际问题的图论模型就是树。 例2 族谱图与树 2、树的应用 要把一个家族的繁衍情况简洁直观表达出来,用点 表示家族中成员,成员x是成员y的儿女,把点x画在点 y的下方,并连线。如此得到的图,是一颗树,称为根 树。示意如下: 根树

实际上,根树是许多问题的模型,如社会结构,计算机 数据结构,数学中的公式结构,分类枚举表示等。 例3道路的铺设与树 假设要在某地建造4个工厂,拟修筑道路连接这4处。 经勘探,其道路可按下图的无向边铺设。现在每条边的 长度已经测出并标记在图的对应边上,如果我们要求铺 设的道路总长度最短,这样既能节省费用,又能缩短 工期,如何铺设? 1V2 4
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 实际上,根树是许多问题的模型,如社会结构,计算机 数据结构,数学中的公式结构,分类枚举表示等。 例3 道路的铺设与树 假设要在某地建造4个工厂,拟修筑道路连接这4处。 经勘探,其道路可按下图的无向边铺设。现在每条边的 长度已经测出并标记在图的对应边上,如果我们要求铺 设的道路总长度最短,这样既能节省费用 ,又能缩短 工期 ,如何铺设? v2 v3 v4 e2 e3 e4 v1 e1 e5 e6

该问题归结于在图中求所谓的最小生成树问题。或 称为赋权图中的最小连接问题。 例4化学中的分子结构与树 例如:CH0的两种同分异构结构图模型为 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 该问题归结于在图中求所谓的最小生成树问题。或 称为赋权图中的最小连接问题。 例4 化学中的分子结构与树 例如:C4H10的两种同分异构结构图模型为: h hh h hhh h h h h hhh h h h h h h

例5电网络中独立回路与图的生成树 早在19世纪,图论还没有引起人们关注的时候,物理学 家克希荷夫就已经注意到电路中的独立回路与该电路中的所 谓生成树的关系。即:如果电路是(m,)图,则独立回路的 个数为m-+1.并且,生成树添上生成树外的G的一条边,就 可以得到一独立回路。 总之,树在图论研究和图论应用上都是十分典型的特殊图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 例5 电网络中独立回路与图的生成树 早在19世纪,图论还没有引起人们关注的时候,物理学 家克希荷夫就已经注意到电路中的独立回路与该电路中的所 谓生成树的关系。即:如果电路是(n, m)图,则独立回路的 个数为m-n+1.并且,生成树添上生成树外的G的一条边,就 可以得到一独立回路。 总之,树在图论研究和图论应用上都是十分典型的特殊图

(二)、树的性质 定理1每棵非平凡树至少有两片树叶。 证明设P-yY2v是非平凡树T中一条最长路,则y1 与v在T中的邻接点只能有一个,否则,要么推出P 不是最长路,要么推出T中存在圈,这都是矛盾! 即说明v,与v是树叶。 定理2图G是树当且仅当G中任意两点都被唯一的路 连接。 证明:“必要性” 若不然,设P与P,是连接u与v的两条不同的路。则 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 定理1 每棵非平凡树至少有两片树叶。 证明 设P=v1v2…vk是非平凡树T中一条最长路,则v1 与vk在T中的邻接点只能有一个,否则,要么推出P 不是最长路,要么推出T中存在圈,这都是矛盾! 即说明v1与v2是树叶。 定理2 图G是树当且仅当G中任意两点都被唯一的路 连接。 证明:“必要性” 若不然,设P1与P2是连接u与v的两条不同的路。则 (二)、树的性质

由这两条路的全部或部分将构成二个圈,这与G是 树相矛盾。 “充分性” 首先,因G的任意两点均由唯一路相连,所以G是连通的。 其次,若G中存在圈,则在圈中任取点u与v,可得 到连接u与v的两条不同的路,与条件矛盾。 定理3设T是(,m)树,则: m=n-1 证明:对n作数学归纳
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 由这两条路的全部或部分将构成一个圈,这与G是 树相矛盾。 “充分性” 首先,因G的任意两点均由唯一路相连,所以G是连通的。 其次,若G中存在圈,则在圈中任取点u与v,可得 到连接u与v的两条不同的路,与条件矛盾。 定理3 设T是(n, m)树,则: m n 1 证明:对n作数学归纳

当n=1时,等式显然成立; 设n=k时等式成立。考虑n=k+1的树T。 由定理1T中至少有两片树叶,设u是T中树叶,考虑 T,=T-u,则T,为k阶树,于是m(T)=k-1,得m(T)=k。 这就证明了定理3。 例6设T为12条边的树,其顶点度为1,2,5。如果T恰有 3个度为2的顶点,那么T有多少片树叶? 解:设T有x片树叶。 由m=n-1得n=13.于是由握手定理得: 1×x+2×3+5×(10-x)=2×12 2
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 12 当n=1时,等式显然成立; 设n=k时等式成立。考虑n=k+1的树T。 由定理1 T中至少有两片树叶,设u是T中树叶,考虑 T1=T-u,则T1为k阶树,于是m(T1)=k-1, 得m(T)=k。 这就证明了定理3。 例6 设T为12条边的树,其顶点度为1,2,5。如果T恰有 3个度为2的顶点,那么T有多少片树叶? 解:设T有x片树叶。 由m=n-1得n=13. 于是由握手定理得: 1 2 3 5 (10 ) 2 12 x x