
本次课主要内容 图的边着色 (一)、相关概念 (二)、几类特殊图的边色数 (三)、边着色的应用
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、相关概念 (二)、几类特殊图的边色数 图的边着色 (三)、边着色的应用

(一)、相关概念 现实生活中很多问题,可以模型为所谓的边着色问题 来处理。例如排课表问题。 排课表问题:设有m位教师,n个班级,其中教师x要 给班级y,上P节课。求如何在最少节次排完所有课。 建模:令X三(x1x2xm),Y={y1N2y},X与y,间 连P条边,得偶图G=(X,Y), 于是,问题转化为如何在G中将边集E划分为互不相交 的p个匹配,且使得p最小。 如果每个匹配中的边用同一种颜色染色,不同匹配中 的边用不同颜色染色,则问题转化为在G中给每条边染 色,相邻边染不同色,至少需要的颜色数
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 现实生活中很多问题,可以模型为所谓的边着色问题 来处理。例如排课表问题。 (一)、相关概念 排课表问题:设有m位教师,n个班级,其中教师xi要 给班级yj上pij节课。求如何在最少节次排完所有课。 建模:令X={x1,x2,…,xm}, Y={y1,y2,…,yn},xi与yj间 连pij条边,得偶图G=(X, Y). 于是,问题转化为如何在G中将边集E划分为互不相交 的p个匹配,且使得p最小。 如果每个匹配中的边用同一种颜色染色,不同匹配中 的边用不同颜色染色,则问题转化为在G中给每条边染 色,相邻边染不同色,至少需要的颜色数
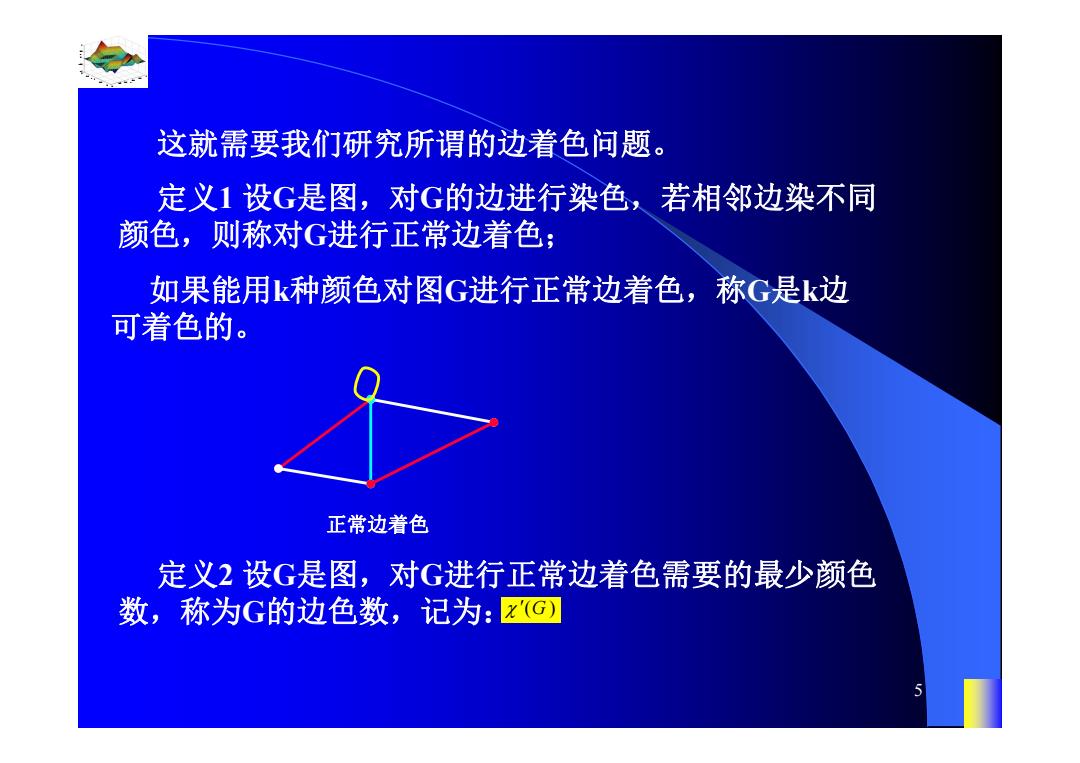
这就需要我们研究所谓的边着色问题。 定义1设G是图,对G的边进行染色,若相邻边染不同 颜色,则称对G进行正常边着色; 如果能用k种颜色对图G进行正常边着色,称G是k边 可着色的。 正常边着色 定义2设G是图,对G进行正常边着色需要的最少颜色 数,称为G的边色数,记为:z©)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 这就需要我们研究所谓的边着色问题。 定义1 设G是图,对G的边进行染色,若相邻边染不同 颜色,则称对G进行正常边着色; 如果能用k种颜色对图G进行正常边着色,称G是k边 可着色的。 正常边着色 定义2 设G是图,对G进行正常边着色需要的最少颜色 数,称为G的边色数,记为: ( ) G

x'(G)=3 注:对图的正常边着色,实际上是对G的边集合的一 种划分,使得每个划分块是G的一个边独立集(无环时是 匹配);图的边色数对应的是图的最小独立集划分数。 因此,图的边着色,本质上是对应实际问题中的“划 分”问题或“分类”问题。 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 注:对图的正常边着色,实际上是对G的边集合的一 种划分,使得每个划分块是G的一个边独立集(无环时是 匹配);图的边色数对应的是图的最小独立集划分数。 () 3 G 因此,图的边着色,本质上是对应实际问题中的“划 分”问题或“分类”问题

在对G正常边着色时,着相同颜色的边集称为该正常 着色的一个色组。 (二)、几类特殊图的边色数 1、偶图的边色数 定理1 X(Kmn)=△ 证明:设 X={xo,x,,xm-} Y=oys..n1 又设△=n。设颜色集合为{0,1,2,…, n-1),Π是 Kn的一种n着色方案,满足: Vx,y,∈E(Km.m),π(x,y,)=(i+j)(modn)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 在对G正常边着色时,着相同颜色的边集称为该正常 着色的一个色组。 (二)、几类特殊图的边色数 1、偶图的边色数 定理1 , ( ) K m n 证明:设 01 1 , ,..., X xx x m 01 1 , ,..., Y yy y n 又设Δ=n。设颜色集合为{0,1,2,…,n-1}, п是 Km,n的一种n着色方案,满足: , ( ), ( ) ( )(mod ) i j mn i j x y EK x y i j n

我们证明:上面的着色是正常边着色。 对Km,m中任意的两条邻接边xy,和xyk。若 π(x,y,)=π(xy) 则:i计j(modn=i+k(modn),得到j=k,矛盾! 所以,上面着色是正常作色。所以: X'(Kmn)≤n 又显然 X'(Kmn)≥△=n ,所以, x'(Kn)=A 例1用最少的颜色数对K3.4正常边着色。 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 我们证明:上面的着色是正常边着色。 对K m, n中任意的两条邻接边xiyj和xiyk。若 ()() i j ik x y x y 则:i+ j ( mod n)=i +k ( mod n),得到j=k,矛盾! 所以,上面着色是正常作色。所以: , ( ) K n m n 又显然 ,所以, , ( ) K n m n , ( ) K m n 例1 用最少的颜色数对K3,4正常边着色

y2 定义3设T是G的一种正常边着色,若点u关联的边的 着色没有用到色i,则称点u缺i色。 定理2(哥尼,1916若G是偶图,则x'(G)=△ 证明:我们对G的边数作数学归纳。 当m=1时,△=1,有x'(G)=△=1
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 定理2 (哥尼,1916)若G是偶图,则 x x2 1 x0 y1 y2 y3 y0 ( ) G 定义3 设п是G的一种正常边着色,若点u关联的边的 着色没有用到色i,则称点u缺i色。 证明:我们对G的边数m作数学归纳。 当m=1时,Δ=1,有 () 1 G

设对于小于m条边的偶图来说命题成立。 设G是具有m条边的偶图。 取v∈E(G),考虑G=G-Y,由归纳假设有: X'(G)=△(G)≤△(G) 这说明,G,存在一种△(G)边着色方案Ⅱ。对于该着色方案, 因为uv未着色,所以点u与v均至少缺少一种色。 情形1如果u与v均缺同一种色i,则在G,+v中给uv着色 i,而G,其它边,按Π方案着色。这样得到G的△着色方案 所以: x'(G)=△ 情形2如果u缺i色,但不缺j色;而v缺i色,但不缺i色。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 设G是具有m条边的偶图。 设对于小于m条边的偶图来说命题成立。 取uv∈ E(G), 考虑G1=G-uv,由归纳假设有: 这说明,G1存在一种Δ(G)边着色方案п。对于该着色方案, 因为uv未着色,所以点u与v均至少缺少一种色。 1 1 ( ) ( ) () GGG 情形1 如果u与v均缺同一种色i, 则在G1+uv中给uv着色 i, 而G1其它边,按п方案着色。这样得到G的Δ着色方案, 所以: ( ) G 情形2 如果u缺i色, 但不缺j色; 而v缺j色,但不缺i色

设H(,)表示G,中由色边与j色边导出的子图。显然, 该图每个分支是色边和色边交替出现的路或圈。 对于H(i,j)中含点v的分支来说,因v缺色j,但不缺色i, 所以,在H(i,)中,点v的度数为1。这说明,Hi,j)中含y 的分支是一条路P。 进一步地,我们可以说明,上面的路P不含点u。 因为,如果P含有点u,那么P必然是一条长度为偶数的 路,这样,P+v是G中的奇圈,这与G是偶图矛盾! 既然P不含点u,所以我们可以交换P中着色,而不破坏 G,的正常边着色。但交换着色后,u与v均缺色i,于是由 情形1,可以得到G的△正常边着色,即证明:x(G)=△
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 设H (i, j) 表示G1中由i色边与j色边导出的子图。显然, 该图每个分支是i色边和j色边交替出现的路或圈。 对于H(i, j)中含点v的分支来说,因v缺色j, 但不缺色i, 所以,在H(i, j)中,点v的度数为1。这说明,H(i ,j)中含v 的分支是一条路P。 进一步地,我们可以说明,上面的路P不含点u。 因为,如果P含有点u, 那么P必然是一条长度为偶数的 路,这样,P+uv是G中的奇圈,这与G是偶图矛盾! 既然P不含点u, 所以我们可以交换P中着色,而不破坏 G1的正常边着色。但交换着色后,u与v均缺色i, 于是由 情形1,可以得到G的Δ正常边着色,即证明:( ) G
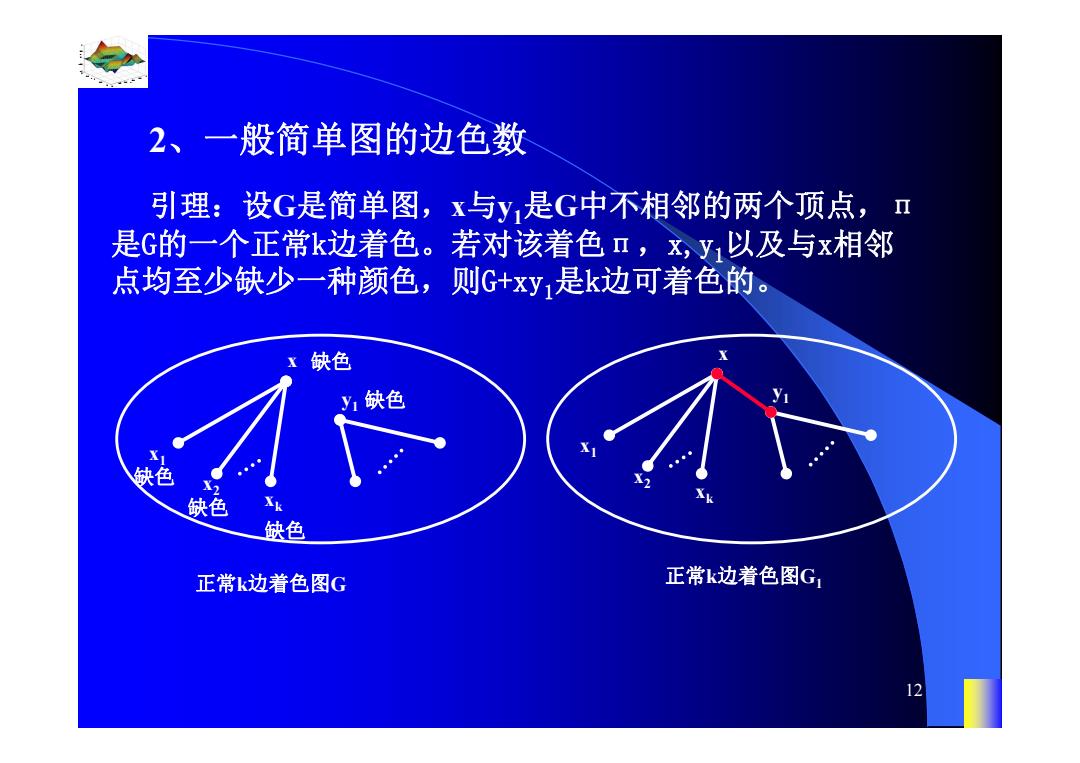
2、一般简单图的边色数 引理:设G是简单图,x与y,是G中不相邻的两个顶点,Ⅱ 是G的一个正常k边着色。若对该着色Π,x,y1以及与x相邻 点均至少缺少一种颜色,则G+xy是k边可着色的。 缺色 y1缺色 缺色 缺色 正常k边着色图G 正常k边着色图G 12
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 12 2、一般简单图的边色数 引理:设G是简单图,x与y1是G中不相邻的两个顶点,п 是G的一个正常k边着色。若对该着色п,x,y1以及与x相邻 点均至少缺少一种颜色,则G+xy1是k边可着色的。 正常k边着色图G x1 y1 x x2 xk 缺色 缺色 缺色 缺色 缺色 正常k边着色图G1 x1 y1 x x2 xk