
本次课主要内容 期末复习 (一)、重点概念 (二)、重要结论 (三)、应用
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (二)、重要结论 期末复习 (一)、重点概念 (三)、应用

(一)、重点概念 1、图、简单图、图的同构与自同构、度序列与图序列、 补图与自补图、两个图的联图、两个图的积图、偶图; (1)图:一个图是一个序偶,记为G=(V,E),其中: 1)V是一个有限的非空集合,称为顶点集合,其元素称为顶点或点。 用|V表示顶点数; 2)E是由V中的点组成的无序对构成的集合,称为边集,其元素称 为边,且同一点对在卫中可以重复出现多次。用E表示边数。 (2)简单图:无环无重边的图称为简单图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 (一)、重点概念 1、图、简单图、图的同构与自同构、度序列与图序列、 补图与自补图、两个图的联图、两个图的积图、偶图; (1) 图:一个图是一个序偶,记为G=(V,E),其中: 1) V是一个有限的非空集合,称为顶点集合,其元素称为顶点或点。 用|V|表示顶点数; 2) E是由V中的点组成的无序对构成的集合,称为边集,其元素称 为边,且同一点对在E中可以重复出现多次。用|E|表示边数。 (2) 简单图:无环无重边的图称为简单图

(3) 图的度序列: 一个图G的各个点的度d,d2,,dn构成的非负整数组(d,d2,,dn) 称为G的度序列。 注:度序列的判定问题是重点。 (4图的图序列: 一个非负数组如果是某简单图的度序列,我们称它为可图序列,简 称图序列。 注:图序列的判定问题是重点。 (⑤)图的同构:
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 (3) 图的度序列: 一个图G的各个点的度d1, d2,…, dn构成的非负整数组(d1, d2,…, dn) 称为G的度序列 。 注:度序列的判定问题是重点。 (4) 图的图序列: 一个非负数组如果是某简单图的度序列,我们称它为可图序列,简 称图序列。 注:图序列的判定问题是重点。 (5) 图的同构:

设有两个图G=(V,E)和G2=(V2,E2),若在其顶点集合间存在双射,使得边 之间存在如下关系:设u1→u2Y1→V2,u1∈V1,u2,Y2∈V2uV1∈E1,当 且仅当u2Y2∈E2,且uV,与u2Y2的重数相同。称G,与G2同构,记为: G1¥G2 例1指出4个顶点的非同构的所有简单图。 分析:四个顶点的简单图最少边数为0,最多边数为6,所以 可按边数进行枚举。 11
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 设有两个图G1=(V1,E1)和G2=(V2,E2),若在其顶点集合间存在双射,使得边 之间存在如下关系:设u1↔u2v1↔v2, u1,v1 V1, u2,v2 V2; u1v1 E1,当 且仅当u2v2 E2 ,且u1v1与u2v2的重数相同。称G1与G2同构,记为: G G 1 2 例1 指出4个顶点的非同构的所有简单图。 分析:四个顶点的简单图最少边数为0,最多边数为6,所以 可按边数进行枚举
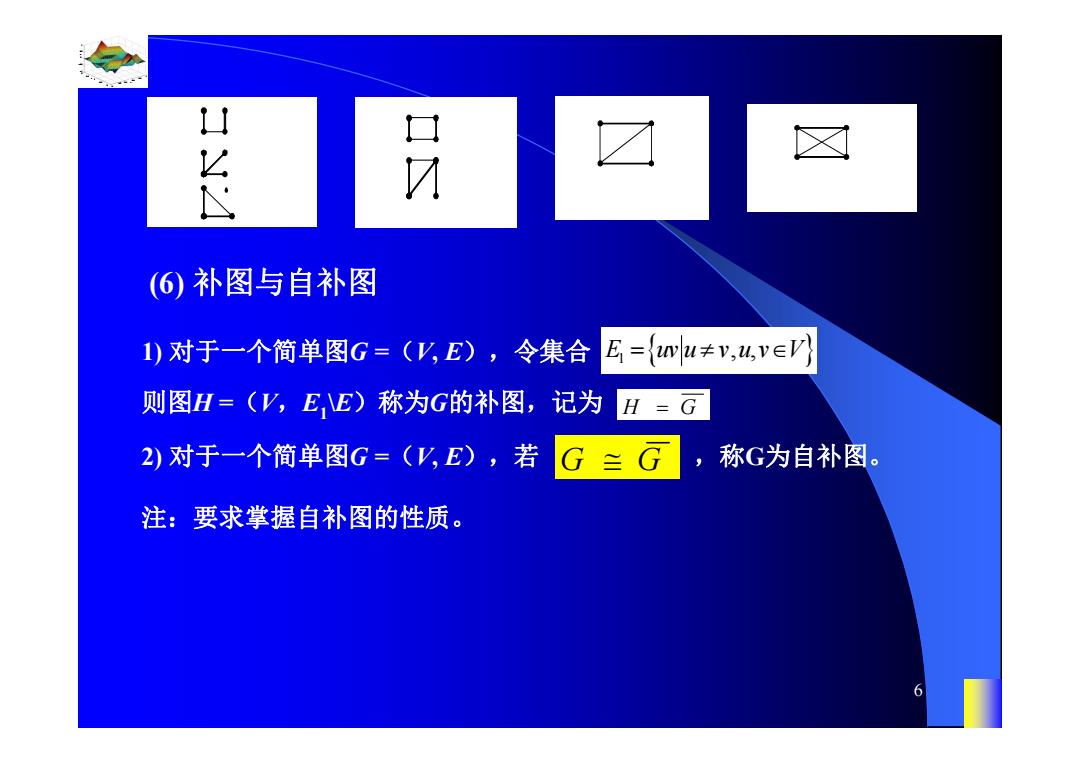
山 ∠ 口7 (6)补图与自补图 1)对于一个简单图G=(V,E),令集合 E={wlu≠v,4,v∈V旷 则图H=(V,EE)称为G的补图,记为H=G 2)对于一个简单图G=(V,E),若 G G, 称G为自补图。 注:要求掌握自补图的性质。 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 (6) 补图与自补图 1) 对于一个简单图G =(V, E),令集合 E1 uv u v u v V , , 则图H =(V,E1\E)称为G的补图,记为 H G 2) 对于一个简单图G =(V, E),若 ,称 G G G为自补图。 注:要求掌握自补图的性质

(⑦联图 设G1,G,是两个不相交的图,作G+G,并且将G,中每个顶点和G2 中的每个顶点连接,这样得到的新图称为G,与G,的联图。记为: (⑧)积图 设G1=(V1,E1),G2=(V2,E2) 是两个图。对点集V=V,×V2 的任意两个点u=(u1,u2)与v=(Wv2,当(u1=v和u2adjv2)或(u2=V2和 u1adjv)时,把u与v相连。如此得到的新图称为G,与G2的积图。 记为 G =G1×G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 (7) 联图 设G1,G2是两个不相交的图,作G1+G2,并且将G1中每个顶点和G2 中的每个顶点连接,这样得到的新图称为G1与G2的联图。记为 : G G 1 2 (8) 积图 设 是两个图。对点集 1 11 2 2 2 G VE G V E ( , ), ( , ), V VV 1 2 的任意两个点u=(u1,u2)与v=(v1,v2),当(u1=v1和u2adjv2)或(u2=v2和 u1adjv1)时,把u与v相连。如此得到的新图称为G1与G2的积图。 记为 GGG 1 2

(⑨)偶图 所谓具有二分类(X,Y)的偶图(或二部图)是指一个图,它的点 集可以分解为两个(非空)子集和Y,使得每条边的一个端点在中,另 一个端点在Y中 注:掌握偶图的判定。 2、树、森林,生成树,最小生成树、根树、完全m元树。 (1)树 不含圈的图称为无圈图,树是连通的无圈图。 (2)森林 称无圈图G为森林。 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 (9) 偶图 所谓具有二分类(X, Y)的偶图(或二部图)是指一个图,它的点 集可以分解为两个(非空)子集X和Y,使得每条边的一个端点在中,另 一个端点在Y中. 注: 掌握偶图的判定。 2、树、森林,生成树,最小生成树、根树、完全m元树。 (1) 树 不含圈的图称为无圈图,树是连通的无圈图。 (2) 森林 称无圈图G为森林

3)生成树 图G的一个生成子图T如果是树,称它为G的一棵生成树;若1 为森林,称它为G的一个生成森林。 生成树的边称为树枝,G中非生成树的边称为弦。 (4)最小生成树 在连通边赋权图G中求一棵总权值最小的生成树。该生成树称 为最小生成树或最小代价树。 注:要求熟练掌握最小生成树的求法。 (⑤根树 一棵非平凡的有向树T,如果恰有一个顶点的入度为0,而其余所有顶 点的入度为1,这样的的有向树称为根树。其中入度为0的点称为树根, 出度为0的点称为树叶,入度为1,出度大于或等于1的点称为内点。又 将内点和树根统称为分支点。 9
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 (3) 生成树 图G的一个生成子图T如果是树,称它为G的一棵生成树;若T 为森林,称它为G的一个生成森林。 生成树的边称为树枝,G中非生成树的边称为弦。 (4) 最小生成树 在连通边赋权图G中求一棵总权值最小的生成树。该生成树称 为最小生成树或最小代价树。 注:要求熟练掌握最小生成树的求法。 (5) 根树 一棵非平凡的有向树T,如果恰有一个顶点的入度为0,而其余所有顶 点的入度为1,这样的的有向树称为根树。其中入度为0的点称为树根, 出度为0的点称为树叶,入度为1,出度大于或等于1的点称为内点。又 将内点和树根统称为分支点

(6)完全m元树 对于根树T,若每个分支点至多m个儿子,称该根树为m元根树; 若每个分支点恰有m个儿子,称它为完全m元树。 注:对于完全m元树,要弄清其结构。 3、途径(闭途径),迹(闭迹),路(圈),最短路,连通图,连 通分支,点连通度与边连通度。 注:上面概念分别在1和3章 4、欧拉图,欧拉环游,欧拉迹,哈密尔顿圈,哈密尔顿 图,哈密尔顿路,中国邮路问题,最优H圈。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 (6) 完全m元树 对于根树T,若每个分支点至多m个儿子,称该根树为m元根树; 若每个分支点恰有m个儿子,称它为完全m元树。 注:对于完全m元树,要弄清其结构。 3、途径(闭途径),迹(闭迹), 路(圈), 最短路,连通图,连 通分支,点连通度与边连通度。 注:上面概念分别在1和3章 4、欧拉图,欧拉环游,欧拉迹,哈密尔顿圈,哈密尔顿 图,哈密尔顿路,中国邮路问题,最优H圈

(1)! 欧拉图与欧拉环游 对于连通图G,如果G中存在经过每条边的闭迹,则称G为欧 拉图,简称G为E图。欧拉闭迹又称为欧拉环游,或欧拉回路。 (2)欧拉迹 对于连通图G,如果G中存在经过每条边的迹, 则称该迹为G 的一条欧拉迹。 (3)哈密尔顿图与哈密尔顿圈 如果经过图G的每个顶点恰好一次后能够回到出发点,称这样 的图为哈密尔顿图,简称H图。所经过的闭途径是G的一个生成圈, 称为G的哈密尔顿圈。 (4)哈密尔顿路 图G的经过每个顶点的路称为哈密尔顿路
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 (1) 欧拉图与欧拉环游 (2) 欧拉迹 对于连通图G,如果G中存在经过每条边的闭迹,则称G为欧 拉图,简称G为E图。欧拉闭迹又称为欧拉环游,或欧拉回路。 对于连通图G,如果G中存在经过每条边的迹,则称该迹为G 的一条欧拉迹。 (3) 哈密尔顿图与哈密尔顿圈 如果经过图G的每个顶点恰好一次后能够回到出发点,称这样 的图为哈密尔顿图,简称H图。所经过的闭途径是G的一个生成圈, 称为G的哈密尔顿圈。 (4) 哈密尔顿路 图G的经过每个顶点的路称为哈密尔顿路