
Advanced Algorithms Balls into Bins 尹一通Nanjing University,202Fall
尹⼀通 Nanjing University, 202 Fall Advanced Algorithms Balls into Bins
Balls into Bins n balls uniform independent m bins 44↓4↓444 random function f:[n][m] birthday,coupon collector,occupancy
Balls into Bins n balls m bins uniform & independent birthday, coupon collector, occupancy, ... random function f : [n] → [m]
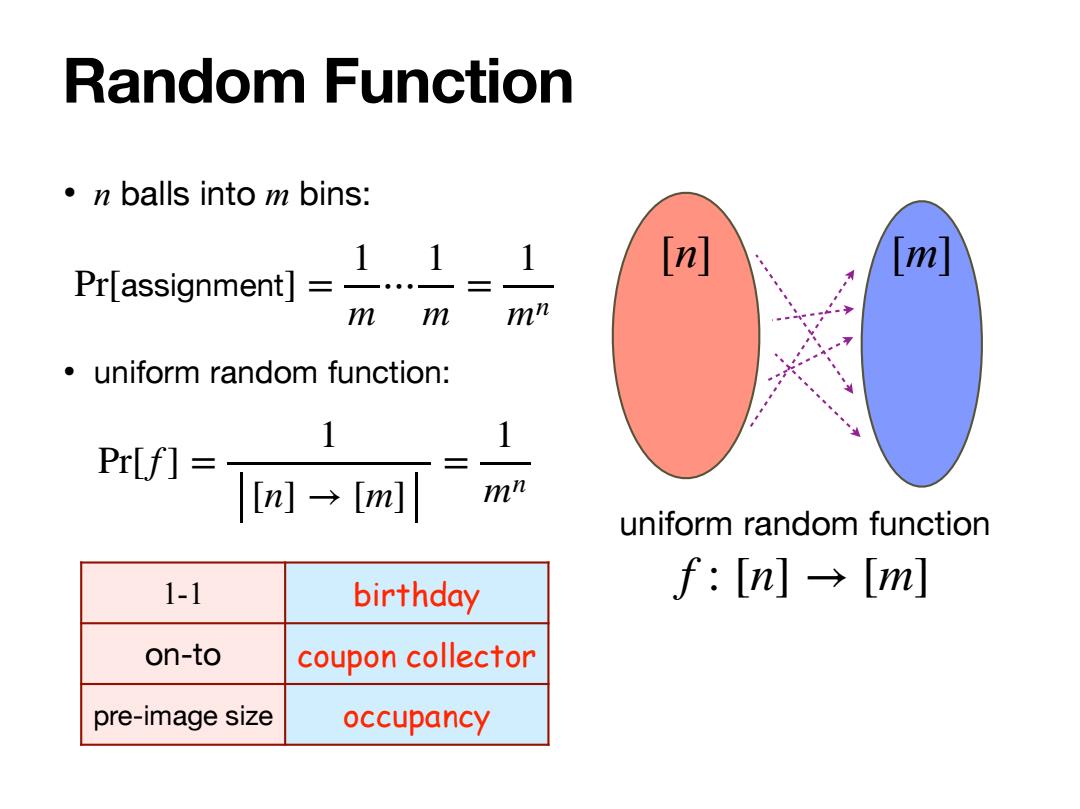
Random Function ·n balls into m bins: Pr(assignment]=1. 1 [m] [m] mm mn uniform random function: 1 1 Pr[f]= [m→m] mn uniform random function 1-1 birthday f:[n]→[m] on-to coupon collector pre-image size occupancy
Random Function • n balls into m bins: • uniform random function: Pr[assignment] = 1 m ⋯ 1 m = 1 mn Pr[f ] = 1 [n] → [m] = 1 mn [n] [m] uniform random function f : [n] → [m] 1-1 birthday on-to coupon collector pre-image size occupancy

Birthday Paradox Paradox: (i)a statement that leads to a contradiction; (ii)a situation which defies intuition. In a class of m>57 students,with >99%probability, there are two students with the same birthday. Assumption:birthdays are uniformly independently distributed. n balls are thrown into m bins: event each bin receives 1 balls
Birthday Paradox Paradox: (i) a statement that leads to a contradiction; (ii) a situation which defies intuition. In a class of m>57 students, with >99% probability, there are two students with the same birthday. Assumption: birthdays are uniformly & independently distributed. n balls are thrown into m bins: event ℰ: each bin receives ≤ 1 balls

Birthday Paradox n balls are thrown into m bins: event each bin receives 1 balls m与[ m(m-1)…(m-n+1) Pr[8]= [n→m mn i(-)
Birthday Paradox Pr[ℰ] = [n] 1−1 [m] [n] → [m] = m(m − 1)⋯(m − n + 1) mn = n−1 ∏ i=0 (1 − i m ) n balls are thrown into m bins: event ℰ: each bin receives ≤ 1 balls

Birthday Paradox n balls are thrown into m bins: event each bin receives 1 balls Suppose that balls are thrown one-by-one: Pr[]=Pr[all n balls are thrown into ditinct bins] chain Pr[the ith ball is thrown into an empty bin rule =1 first i-1 balls are thrown into ditinct bins] (--i0-)
Birthday Paradox Pr[ℰ] = Pr[all n balls are thrown into ditinct bins] = n ∏ i=1 Pr[the ith ball is thrown into an empty bin ∣ first i − 1 balls are thrown into ditinct bins] Suppose that balls are thrown one-by-one: = n ∏ i=1 (1 − i − 1 m ) = n−1 ∏ i=0 (1 − i m) n balls are thrown into m bins: event ℰ: each bin receives ≤ 1 balls chain rule

Birthday Paradox n balls are thrown into m bins: event each bin receives 1 balls (Taylor:1-xe*forx=o(1)) PT61= (-)i。n i0 Formaly::≤i(l-月)setm2 (assuming n <m) whenn=2m in →Pr[8]=(1±o(1)p
Birthday Paradox Pr[ℰ] = n−1 ∏ i=0 (1 − i m) ≈ n−1 ∏ i=0 e− i m ≈ e−n2/2m e−(1+o(1))n2/2m ≤ n−1 ∏ i=0 (1 − i m) ≤ e−(1−o(1))n2/2m (Taylor: 1 − x ≈ e for ) −x x = o(1) Formally: (assuming n ≪ m) when n = 2m ln 1 p ⟹ Pr[ℰ] = (1 ± o(1))p n balls are thrown into m bins: event ℰ: each bin receives ≤ 1 balls

Birthday Paradox n balls are thrown into m bins: event each bin receives 1 balls exacl 0.8 ---approx P阁=计(-) 0.6 n=365 0.4 0.2 0 10 20 30 40 0 60 Formally:e-(1+0(1))n212m 0.02 0 (assuming n m) 0.02 10 2030 4050 60 m when n =12 → Pr[8]=(1±o(1)p
Birthday Paradox Pr[ℰ] = n−1 ∏ i=0 (1 − i m) ≈ n−1 ∏ i=0 e− i m ≈ e−n2/2m e−(1+o(1))n2/2m ≤ n−1 ∏ i=0 (1 − i m) ≤ e−(1−o(1))n2/2m (Taylor: 1 − x ≈ e for ) −x x = o(1) Formally: (assuming n ≪ m) when n = 2m ln 1 p ⟹ Pr[ℰ] = (1 ± o(1))p n balls are thrown into m bins: event ℰ: each bin receives ≤ 1 balls

Data Structure for Set Data:a set S of n itemsx,...,=[N] Query:an itemx∈UU Determine whether x E S. Space cost:size of data structure (in bits) entropy of a set:O(n log N)bits (when N>n) Time cost:time to answer a query (in memory accesses) Balanced tree:O(n log N space,O(log n)time Perfect hashing:O(n log N space,O(1)time
Data Structure for Set Data: a set of items Query: an item Determine whether . S n x1, x2, …, xn ∈ U = [N] x ∈ U x ∈ S • Space cost: size of data structure (in bits) • entropy of a set: O(n log N) bits (when N≫n) • Time cost: time to answer a query (in memory accesses) • Balanced tree: O(n log N) space, O(log n) time • Perfect hashing: O(n log N) space, O(1) time
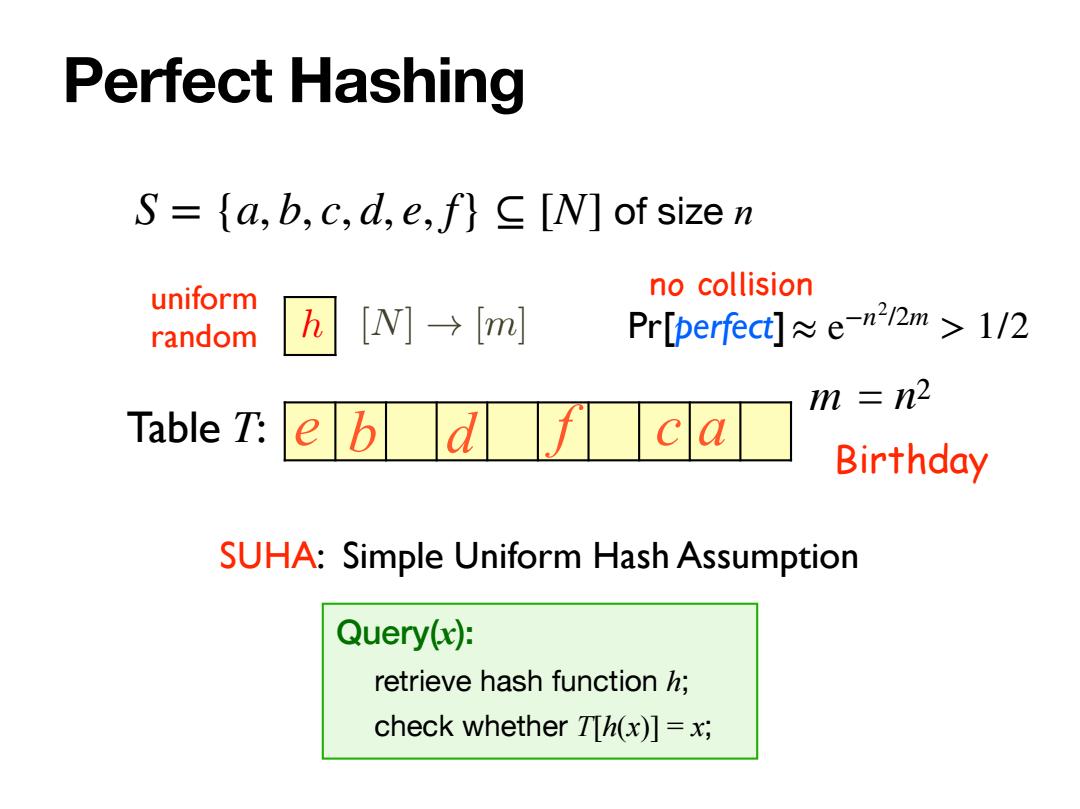
Perfect Hashing S=fa,b,c,d,e,f}C [N]of size n uniform no collision random h [Ny→ml Pr[perfect]e-n22m 1/2 m n2 Table T: e b d ca Birthday SUHA:Simple Uniform Hash Assumption Query(x): retrieve hash function h; check whether TTh(x)]=x;
Perfect Hashing S = {a, b, c, d, e, f} ⊆ [N] of size n e b d f c a h Table T: m uniform random Pr[perfect] Birthday = n2 [N] ! [m] SUHA: Simple Uniform Hash Assumption no collision Query(x): retrieve hash function h; check whether T[h(x)] = x; ≈ e−n2/2m > 1/2