
§4.3随机过程的均方极限与均方连续 本节将二阶矩随机变量空间中的均方极 限概念引入二阶矩随机过程中,并引进均方 连续的概念 一、二阶矩过程 二阶矩过程是一类重要的随机过程, 在物理、生物、通讯与控制、系统工程 与管理科学等方面,有广泛的应用 电子科技大学
电子科技大学 §4.3 随机过程的均方极限与均方连续 本节将二阶矩随机变量空间中的均方极 限概念引入二阶矩随机过程中,并引进均方 连续的概念. 一、二阶矩过程 二阶矩过程是一类重要的随机过程, 在物理、生物、通讯与控制、系统工程 与管理科学等方面,有广泛的应用

1)随机过程的概率性质由其分布函数族 完全确定,但在实际问题中很难确定出分 布函数族 2)正态随机过程的一、二阶矩就能完全 确定其有限维分布. 3)不少实际问题通过对二阶矩的讨论就 足以了解过程的统计特征, 电子科技大学
电子科技大学 1)随机过程的概率性质由其分布函数族 完全确定,但在实际问题中很难确定出分 布函数族. 2)正态随机过程的一、二阶矩就能完全 确定其有限维分布. 3)不少实际问题通过对二阶矩的讨论就 足以了解过程的统计特征

定义4.3.1如过程X={X(t),t∈T仍,对任意 t∈T,有 E{X(t)2}<+o0 称过程是二阶矩过程 二阶矩过程的均值函数和协方差函数一定存在 注 随机变量矩性质: 高阶矩存在则低阶矩及其他同阶一定 存在。 正态过程是二阶矩过程 电子科技大学
电子科技大学 定义4.3.1 如过程XT ={X( t ), t∈T}, 对任意 t∈T, 有 { ( ) } 2 E X t 称过程是二阶矩过程.. 二阶矩过程的均值函数和协方差函数一定存在. 高阶矩存在则低阶矩及其他同阶一定 存在. 注 随机变量矩性质: 正态过程是二阶矩过程

EX.1余弦波过程X(t)=Ac0s(o什⊙),0. 振幅A与角频率Q取常数,相位⊙~U(-元,+π) 因EXd2=A2cos2(wt+0)2元d8≤A,vt≥0, 故X()是一个二阶矩过程. 且 EX()=Acos(t+0d-0. 元 → R(s,t)=E[X(t)X(s) -cos(x0)cs 2元 电子科技大学
电子科技大学 EX.1 余弦波过程X( t )=Acos(ωt+Q), t≥0. 振幅A与角频率ω取常数,相位Q~U(-p, + p) 故 X(t)是一个二阶矩过程. p p p 0, 2 1 且 E{X(t)} Acos( t ) d R(s,t) E[X(t)X(s)] ] 2 1 cos( )cos( ) 2 p p p A t s d

coso(t-s)=IAcosor,(t=t-s) 2 2 二、二阶矩过程的均方极限 定义4.3.2设{X(t),t∈T是二阶矩过程, X∈H,如果 Ii四dX(,X)=mX-X=0 t→to 称X(t)均方收敛于X,记为l.imX(t)=X t-→to 注 l.i.mX(t)=X成立的充分必要条件是 t→to 电子科技大学
电子科技大学 1 2 1 2 cos ( ) cos , 2 2 A t s A ( t s) 二、二阶矩过程的均方极限 定义4.3.2 设{X(t), t∈T}是二阶矩过程, X∈H, 如果 lim ( ( ), ) lim ( ) 0 0 0 d X t X X t X t t t t 称X(t) 均方收敛于X,记为 X t X t t l.i.m ( ) 0 注

对任意的数列{tk,若tk→to(k→oo),有 L.i.m X(t)=X k-→+00 随机过程有类似随机变量序列 的均方收敛意义下的性质。 定理4.3.1(洛易夫均方收敛准则) X()在处收敛的充分必要条件是极限 IimE(X(s)X(t)存在, 二重极限 s,t→to 电子科技大学
电子科技大学 l.i.m ( ) k k X t X 随机过程有类似随机变量序列 的均方收敛意义下的性质. 定理4.3.1(洛易夫均方收敛准则) X(t)在t0处收敛的充分必要条件是极限 二重极限

二、二阶矩过程的均方连续 定义4.3.3称二阶矩过程{X(t),t∈T在 t,∈T处均方连续,如果 Li.m X(t)=X(to) t-→to 若X(t)对Vt∈T都均方连续,称随机过程 X(t),t∈T 是均方连续的。 电子科技大学
电子科技大学 二、二阶矩过程的均方连续 定义4.3.3 称二阶矩过程{X(t), t∈T}在 t0∈T处均方连续, 如果 l.i.m ( ) ( ) 0 0 X t X t t t 若X(t)对t T 都均方连续,称随机过程 {X(t) , t∈T} 是均方连续的

定理4.3.2(均方连续准则) 二阶矩过程{X(t),t∈T在t,∈T处连续的充 分必要条件是{X(),t∈T的相关函数R(S,)在 (,t)处连续. 证由均方收敛准则知 定理4.3.1及均 方连续定义 Li.m X(t)=X(to) t→t0 台limE(X(s)X(t)=EX(t)X(t,)】 s,t→to 即 lim R(s,t)=R(to,to). s,t→to 电子科技大学
电子科技大学 定理4.3.2 (均方连续准则) 二阶矩过程{X(t), t∈T}在t0∈T 处连续的充 分必要条件是{X(t), t∈T}的相关函数R(s,t) 在 (t0 , t0)处连续. 证 由均方收敛准则知 l.i.m ( ) ( ) 0 0 X t X t t t lim ( ( ) ( )) [ ( ) ( )] 0 0 , 0 E X s X t E X t X t s t t 定理4.3.1及均 方连续定义 lim ( , ) ( , ). 0 0 , 0 R s t R t t s t t 即
均方连续准则的重要性: 二阶矩过程的均方连续可由其相关函数的 普通意义下的连续性来确定, 参见P88定 均方连续的重要结论: 理4的证明. 定理4.3.3二阶矩过程的均方连续 相关函数R(S,)在对角线上连续. 推论1二阶矩过程{X(),t∈T的相关函数 R(s,)对t∈T在点(,)处连续,则它在TXT 上连续。 电子科技大学
电子科技大学 参见P88定 理4的证明. 定理4.3.3 二阶矩过程的均方连续 相关函数R(s, t)在对角线上连续. 均方连续准则的重要性: 二阶矩过程的均方连续可由其相关函数的 普通意义下的连续性来确定. 推论1 二阶矩过程{X(t), t∈T}的相关函数 R(s,t) 对 t T 在点(t, t)处连续, 则它在T×T 上连续. 均方连续的重要结论:
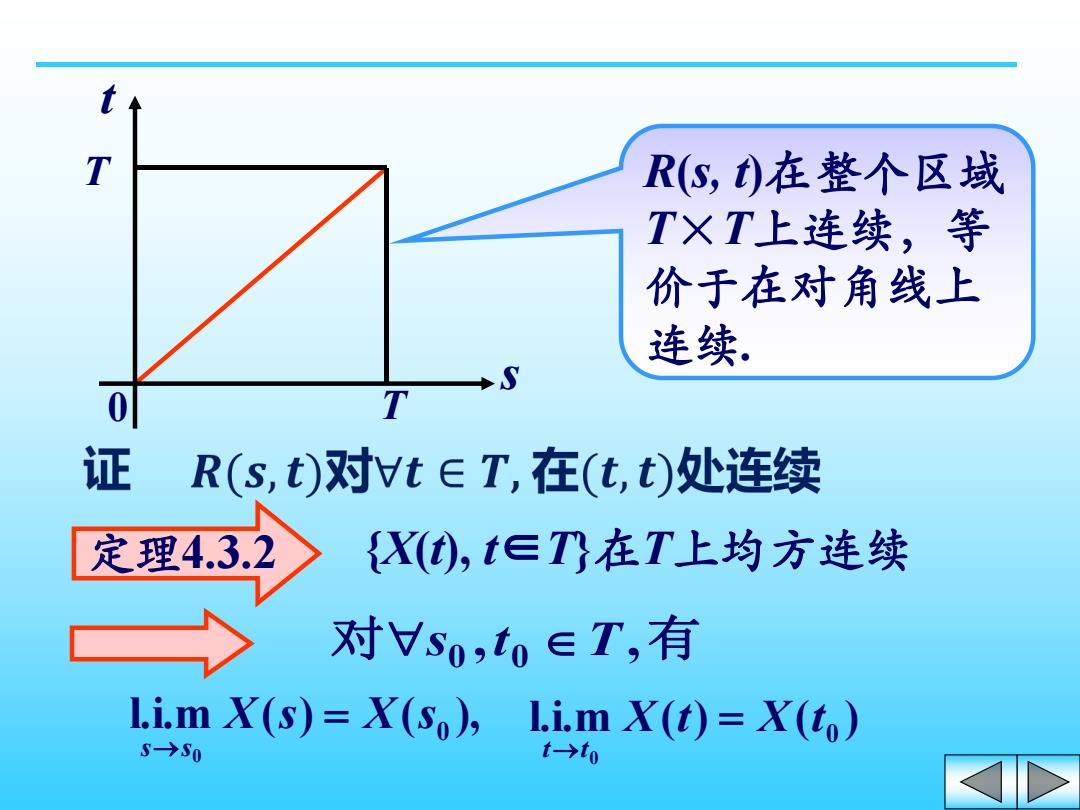
T R(S,)在整个区域 TXT上连续,等 价于在对角线上 连续. S 0 T 证 R(s,t)对vt∈T,在(t,t)处连续 定理4.3.2 {X(t),t∈T在T上均方连续 对s0,t0∈T,有 l.imX(s)=X(so)为 l.i.mX(t)=X(to)》 S→S0 t→to
0 T T t s R(s, t)在整个区域 T×T上连续,等 价于在对角线上 连续. 定理4.3.2 {X(t), t∈T}在T上均方连续 对s0 ,t0 T,有 l.i.m ( ) ( ), 0 0 X s X s s s l.i.m ( ) ( ) 0 0 X t X t t t