
随机过程的基本类型 §2.4随机过程的基本类型 随机过程的基本类型 定义2.4.1对已给(复或实)随机过程{X,t ∈T,若对任意的t∈T,均有E[X2]<+o, 则称{X,t∈T是二阶矩随机过程,简称二 阶过程。 电子科技大学
随机过程的基本类型 电子科技大学 §2.4 随机过程的基本类型 定义2.4.1 对已给(复或实)随机过程{Xt, t ∈T},若对任意的t ∈T,均有E[|Xt|2]<+ ∞, 则称{Xt, t ∈T}是二阶矩随机过程,简称二 阶过程。 一、随机过程的基本类型

随机过程的基本类型 定理2.4.1设随机过程{X,t∈T是二阶矩随 机过程,则其自相关函数满足下列性质 (1)非负性对任意的n≥1及t1,t2,,tn∈T, 对任意的t),t∈T,有 ∑R(t,t)9(:)8(t)≥0 k=1i=1 (2)埃密特对称性(共轭对称性),即 R(s,t)=R(t,s) 电子科技大学
随机过程的基本类型 电子科技大学 定理2.4.1 设随机过程{Xt, t ∈T}是二阶矩随 机过程,则其自相关函数满足下列性质 (1)非负性 对任意的n ≥ 1及t1 ,t2 ,…,tn∈T, 对任意的q(t), t ∈T ,有 ( , ) ( ) ( ) 0 1 1 k j n k n j k j R t t q t q t (2)埃密特对称性(共轭对称性),即 R(s, t ) R(t , s)

随机过程的基本类型 二、独立过程 定义2.4.2 对任意的正整数n及任意的 t1,t2,…,tn∈T,随机变量 (X(t1),X(t2),…,X(tn) 相互独立,称随机过程X(),t∈T)为独立过程. 电子科技大学
随机过程的基本类型 电子科技大学 二、独立过程 ( ( ), ( ), , ( )) 1 2 n X t X t X t

随机过程的基本类型 注独立随机过程的有限维分布由一维分布确定 Fn(G,…,tnx1,…,xn)=ΠF(k;x) k=1 Ex.1高斯白噪声 实值时间序列{X(n),n∈N仍的 E{X(n)}=0, DI(Xn】=o2, 自相关函数为 0, R(m)=, m丰; 两两不相 m=n. 关序列 你{X(n),n∈N}为离散白噪声(序列). 电子科技大学
随机过程的基本类型 电子科技大学 注 独立随机过程的有限维分布由一维分布确定 n k n n n k k k F t t x x F t x 1 1 1 ( ,, ; ,, ) ( ; ) Ex.1 高斯白噪声 { ( )} 0, [( )] , 2 E X n D Xn 自相关函数为 2 0, ; ( , ) , . m n R m n m n 两两不相 关序列

又若X(n)都服从正态分布,称{X(n),n∈N}是 高斯白噪声序列. 对于n维正态随机变量有 相互独立一→不相关 故高斯白噪声序列是独立时间序列, 若过程{X(),t∈R是正态过程,且 EKo-am小-gg0= S≠t 电子科技大学
电子科技大学 对于n维正态随机变量有 故高斯白噪声序列是独立时间序列. EX(t) 0, s t s t R s t s t , 0, ( , ) δ( ) 2

随机过程的基本类型 称其为高斯白噪声过程,它是独立过程, 高斯白噪声是典型的随机千扰数学模型,普 遍存在于电流的波动,通信设备各部分的波 动,电子发射的波动等各种波动现象中. 如金融、电子工程中常用的线性模型 自回归模型(AR(p) X,=9X-1++φpX-p+8, 理想模型要求残差序列8是(高斯)白噪声. 电子科技大学
随机过程的基本类型 电子科技大学 高斯白噪声是典型的随机干扰数学模型,普 遍存在于电流的波动,通信设备各部分的波 动,电子发射的波动等各种波动现象中. 称其为高斯白噪声过程,它是独立过程. 如金融、电子工程中常用的线性模型— 自回归模型(AR(p)) Xt Xt pXt p t 1 1 理想模型要求残差序列εt 是(高斯)白噪声
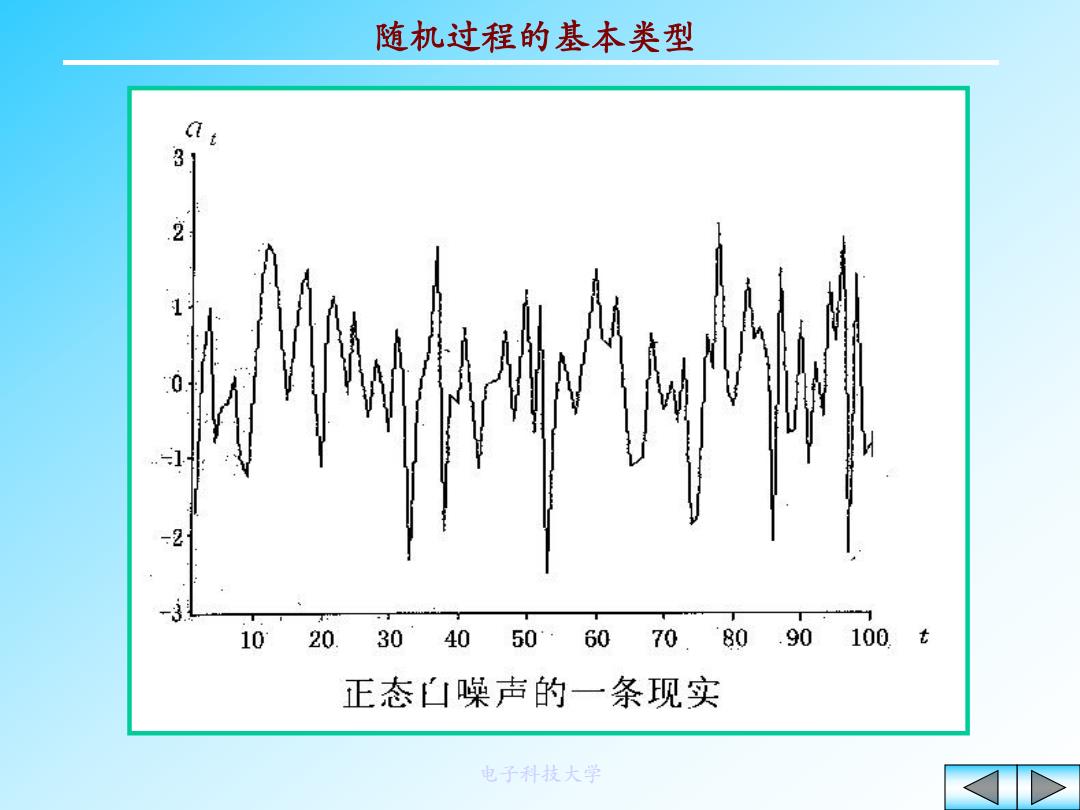
随机过程的基本类型 81 2 1 0 2 1020.304050·6070.8090100t 正态凵噪声的一条现实 电子科技大学
随机过程的基本类型 电子科技大学

三、独立增量过程 定义2.4.3称{X(t),t∈T,T=0,o)为独立 增量过程,若对n≥2,及t。=0<41<42<.<tn,增 量序列 X(t1)-X(0),X(t2)-X(t1),,X(tn)-X(tn-1) 相互独立. 0 电子科技大学
电子科技大学 三、独立增量过程 X(t1) -X(0), X(t2)-X(t1), …, X(tn )-X(tn-1) 相互独立. 0 t1 t2 … tn-1 tn

注不失一般性,设X0)=0或PX(0)=0}=1. 有 Xt1),X(t2)一X(t1),,X(tn)一X(tn-) 相互独立. 定义2.4.4 若独立增量过程{X(),仑0}, 对Vs,t∈T,及h>0, X(t+h)一Xs+)与X)一X(s 有相同的分布函数,称{X(),仑0}是平稳独立 增量过程. S t s+h t什h 0 电子科技大学
电子科技大学 注 不失一般性, 设X(0)=0 或 P{X(0)=0}=1. 有 X(t1) , X(t2)-X(t1), …, X(tn )-X(tn-1) 相互独立. X(t+h) - X(s+h) 与 X(t) - X(s) 有相同的分布函数, 称{X(t),t≥0}是平稳独立 增量过程. 0 s t s+h t+h

注增量X(t+)一X(t)的分布仅与τ有关,与起始 点t无关,称{X(),≥0}的增量具有平稳性(齐性). Ex.2若{X(n),n∈N+}是独立时间序列,令 Yn)=∑x(k), X(0)=0 k=0 则{Y(n),n∈N4}是独立增量过程. 又若X(n),n=1,2,.相互独立同分布,则{Y(m), n∈N+}是平稳独立增量过程. 电子科技大学
电子科技大学 注 Ex.2 若{X(n),n∈N+}是独立时间序列,令 n k Y n X k X 0 ( ) ( ), (0) 0 则{Y(n), n∈N+}是独立增量过程. 又若X(n), n=1,2,… 相互独立同分布,则{Y(n), n∈N+ }是平稳独立增量过程