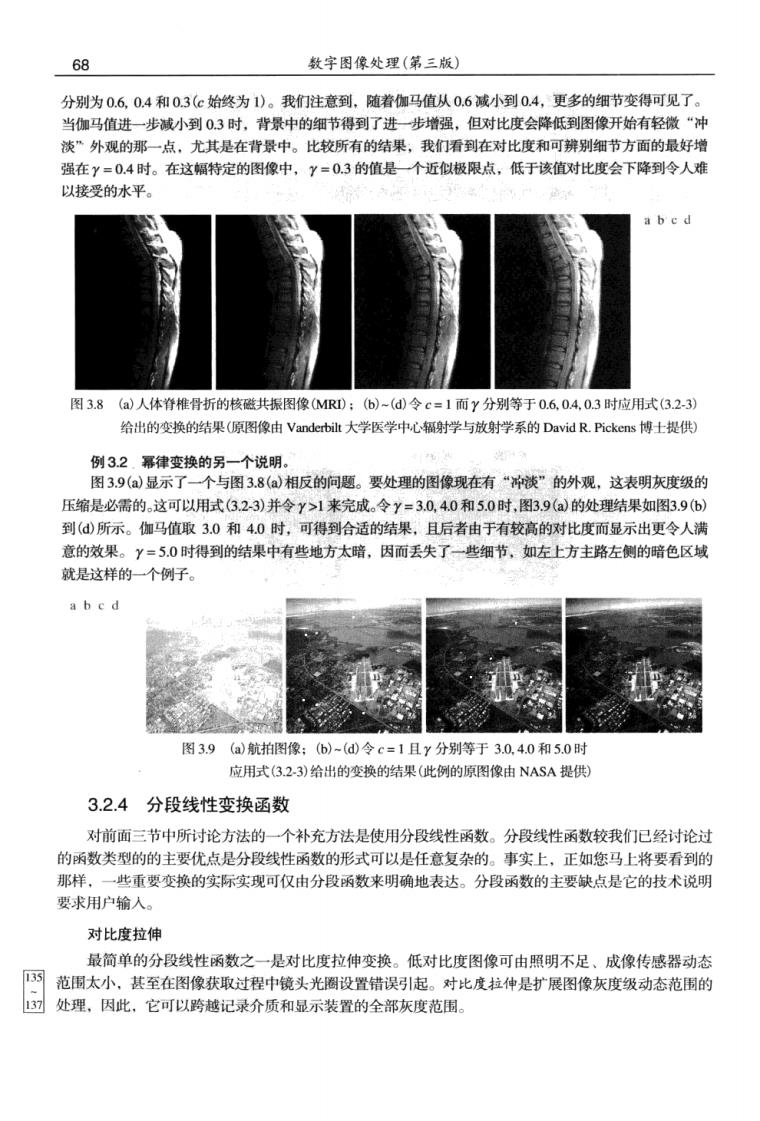
68 数字图像处理（第三版） 分别为0.60,4和0.3(c始终为1)。我们注意到，随着伽马值从0.6减小到0.4，更多的细节变得可见了。 当伽马值进一步诚小到0.3时，背景中的细节得到了进一步增强，但对比度会降低到图像开始有轻微“冲 淡”外观的那一点，尤其是在背景中。比较所有的结果，我们看到在对比度和可辨别细节方面的最好增 强在y=0.4时。在这幅特定的图像中，Y=0.3的值是一个近似极限点，低于该值对比度会下降到令人难 以接受的水平。 a b e d 图3.8(a)人体脊椎骨折的核磁共振图像MRD:(6)-(@令c=1而y分别等于0.60.4,0.3时应用式(3.2-3) 给出的换的结果（原图像由vanderb大学医学中心，辐学与放射学系的David R.Pickens博十提供） 例32.冪律变换的另一个说明。 图3.9()显示了一个与图3.8()相反的向题。要处理的图像现在有“淡”的外观，这表明灰度级的 压缩是必需的。这可以用式3.23)并令y>1来完成。令y=30,40和5.0时，图3,9(a)的处理结果如图3.9(6) 到（所示。伽马值取3.0和4.0时，可得到合适的结果，且后者由于有较高的对比度而显示出更令人满 意的效果。y=5.0时得到的结果中有些地方太暗。.因而丢失了一些细节，如左上方主路左测的暗色区域 就是这样的一个例子 a b e d 图3.9(a)航拍图像：(b)-()令c=1且y分别等于3.0.4.0和5.0时 应用式(3.2.3)给出的变换的结果（此例的原图像由NASA提供 3.2.4分段线性变换函数 对前面三节中所讨论方法的一个补充方法是使用分段线性函数。分段线性函数较我们已经讨论过 的函数类型的的主要优点是分段线性函数的形式可以是任意复杂的。事实上，正如您马上将要看到的 那样。 些重要变换的实际实现可仅由分段函数来明确地表达。分段函数的主要缺点是它的技术说明 要求用户输入。 对比度拉伸 最简单的分段线性函数之一是对比度拉伸变换。低对比度图像可由照明不足、成像传感器动态 网范围太小，甚至在图像获取过程中镜头光圈设置错误马引起。对比度拉仲是扩展图像灰度级动态范围的 园处理，因此。它可以跨越记录介质和显示装置的全部灰度范围