正在加载图片...
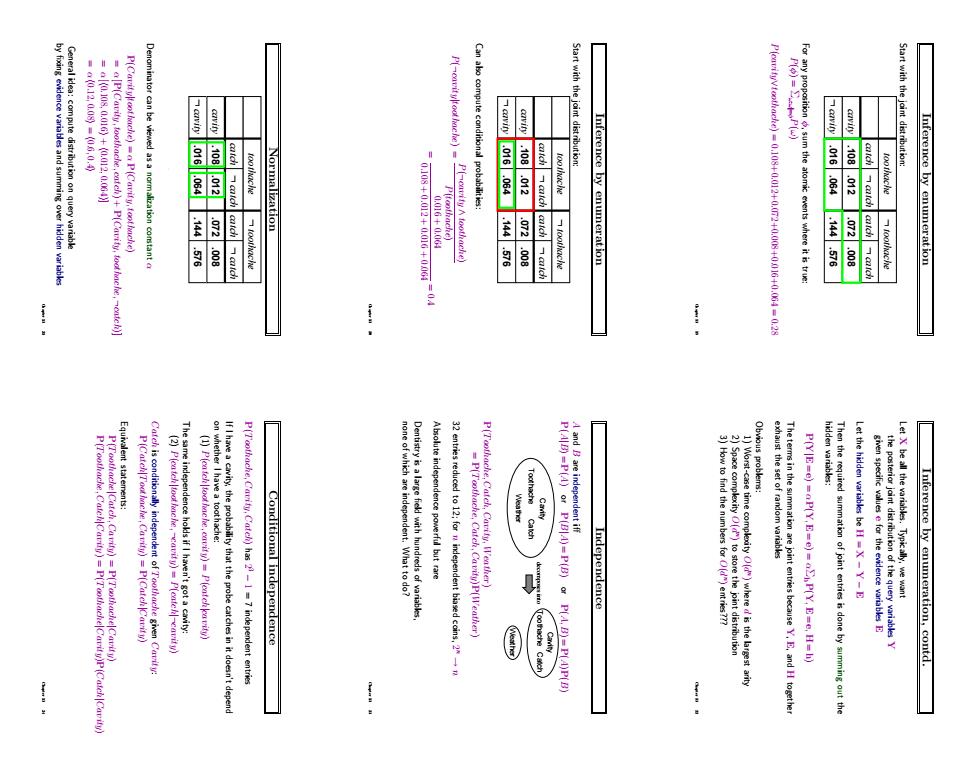
=P(Cavilu,toothache.catch)+P[Cavitu,tod.catch' Start with the joint distrbution 108 .012 -108.m2 .016.064 .10.12 .144.57 he/.94.144.76 .72.009 Inference by enumeration .144-57m .272.008 Inference by enumeration independence but rare the poster da P(Toothache,Carity.Cateh)has-1-7 independent entries Conditional independence Independence Inference by enumeration,contd.Inference by enumeration Start with the joint distribution: cavity L toothache cavity catch catch L toothache L catch catch L .108 .012 .016 .064 .144 .072 .576 .008 For any proposition φ, sum the atomic events where it is true: P(φ) = Σω:ω|=φP(ω) P(cavity∨toothache) = 0.108+0.012+0.072+0.008+0.016+0.064 = 0.28 Chapter 13 19 Inference by enumeration Start with the joint distribution: cavity L toothache cavity catch catch L toothache L catch catch L .108 .012 .016 .064 .144 .072 .576 .008 Can also compute conditional probabilities: P(¬cavity|toothache) = P(¬cavity ∧ toothache) P(toothache) = 0.016 + 0.064 0.108 + 0.012 + 0.016 + 0.064 = 0. Chapter 4 13 20 Normalization cavity L toothache cavity catch catch L toothache L catch catch L .108 .012 .016 .064 .144 .072 .576 .008 Denominator can be viewed as a normalization constant α P(Cavity|toothache) = α P(Cavity,toothache) = α [P(Cavity,toothache, catch) + P(Cavity,toothache,¬catch)] = α [h0.108, 0.016i + h0.012, 0.064i] = α h0.12, 0.08i = h0.6, 0.4i General idea: compute distribution on query variable by fixing evidence variables and summing over hidden variables Chapter 13 21 Inference by enumeration, contd. Let X be all the variables. Typically, we want the posterior joint distribution of the query variables Y given specific values e for the evidence variables E Let the hidden variables be H = X − Y − E Then the required summation of joint entries is done by summing out the hidden variables: P(Y|E = e) = αP(Y, E = e) = αΣhP(Y, E = e, H = h) The terms in the summation are joint entries because Y, E, and H together exhaust the set of random variables Obvious problems: 1) Worst-case time complexity O(d n ) where d is the largest arity 2) Space complexity O(d n ) to store the joint distribution 3) How to find the numbers for O(d n ) entries??? Chapter 13 22 Independence A and B are independent iff P(A|B) = P(A) or P(B|A) = P(B) or P(A, B) = P(A)P(B) Weather Toothache Catch Cavity decomposes into Weather Toothache Catch Cavity P(Toothache, Catch, Cavity, Weather) = P(Toothache, Catch, Cavity)P(Weather) 32 entries reduced to 12; for n independent biased coins, 2 n → n Absolute independence powerful but rare Dentistry is a large field with hundreds of variables, none of which are independent. What to do? Chapter 13 23 Conditional independence P(Toothache, Cavity, Catch) has 2 3 − 1 = 7 independent entries If I have a cavity, the probability that the probe catches in it doesn’t depend on whether I have a toothache: (1) P(catch|toothache, cavity) = P(catch|cavity) The same independence holds if I haven’t got a cavity: (2) P(catch|toothache,¬cavity) = P(catch|¬cavity) Catch is conditionally independent of Toothache given Cavity: P(Catch|Toothache, Cavity) = P(Catch|Cavity) Equivalent statements: P(Toothache|Catch, Cavity) = P(Toothache|Cavity) P(Toothache, Catch|Cavity) = P(Toothache|Cavity)P(Catch|Cavity) Chapter 13 24