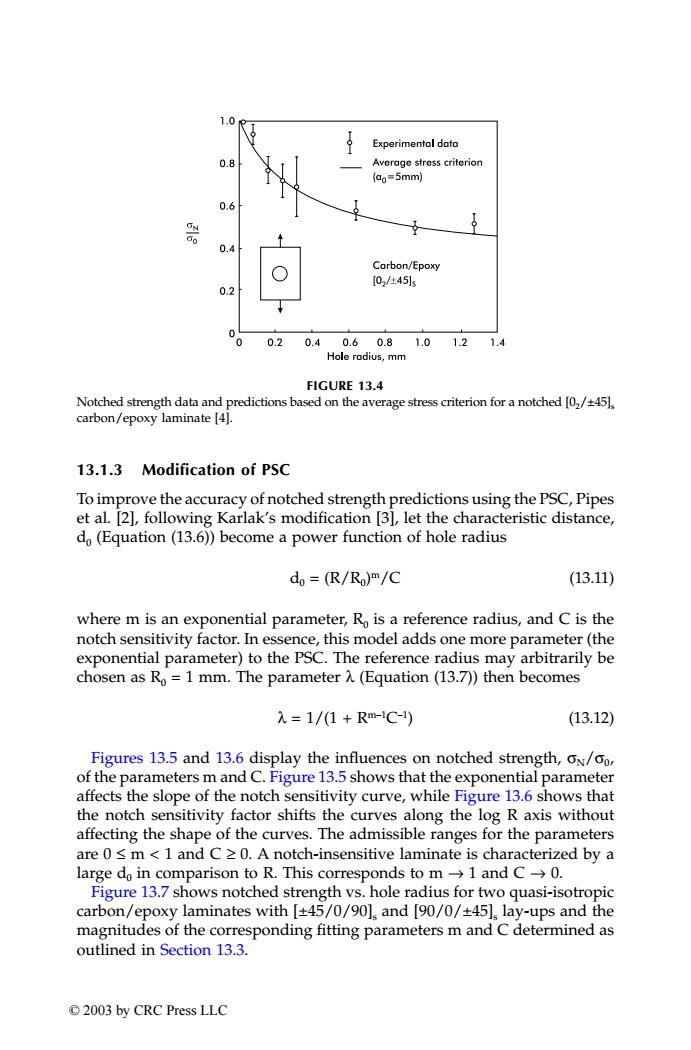
1.0 Experimental dota 0.8 Average stress criterion (ao=5mm) 0.6 ON Carbon/Epoxy [02/±451s 0.2 0 0.2 0.40.60.81.01.21.4 Hole radius,mm FIGURE 13.4 Notched strength data and predictions based on the average stress criterion for a notched [02/45. carbon/epoxy laminate [4]. 13.1.3 Modification of PSC To improve the accuracy of notched strength predictions using the PSC,Pipes et al.[2],following Karlak's modification [3],let the characteristic distance, do(Equation(13.6))become a power function of hole radius do=(R/Ro)m/C (13.11) where m is an exponential parameter,Ro is a reference radius,and C is the notch sensitivity factor.In essence,this model adds one more parameter(the exponential parameter)to the PSC.The reference radius may arbitrarily be chosen as Ro=1 mm.The parameter A(Equation(13.7))then becomes 入=1/(1+Rm-1C-1) (13.12) Figures 13.5 and 13.6 display the influences on notched strength,oN/oo, of the parameters m and C.Figure 13.5 shows that the exponential parameter affects the slope of the notch sensitivity curve,while Figure 13.6 shows that the notch sensitivity factor shifts the curves along the log R axis without affecting the shape of the curves.The admissible ranges for the parameters are 0 s m<1 and C >0.A notch-insensitive laminate is characterized by a large do in comparison to R.This corresponds to m-1 and C->0. Figure 13.7 shows notched strength vs.hole radius for two quasi-isotropic carbon/epoxy laminates with [+45/0/90],and [90/0/+45],lay-ups and the magnitudes of the corresponding fitting parameters m and C determined as outlined in Section 13.3. ©2003 by CRC Press LLC13.1.3 Modification of PSC To improve the accuracy of notched strength predictions using the PSC, Pipes et al. [2], following Karlak’s modification [3], let the characteristic distance, d0 (Equation (13.6)) become a power function of hole radius d0 = (R/R0)m/C (13.11) where m is an exponential parameter, R0 is a reference radius, and C is the notch sensitivity factor. In essence, this model adds one more parameter (the exponential parameter) to the PSC. The reference radius may arbitrarily be chosen as R0 = 1 mm. The parameter λ (Equation (13.7)) then becomes λ = 1/(1 + Rm–1C–1) (13.12) Figures 13.5 and 13.6 display the influences on notched strength, σN/σ0, of the parameters m and C. Figure 13.5 shows that the exponential parameter affects the slope of the notch sensitivity curve, while Figure 13.6 shows that the notch sensitivity factor shifts the curves along the log R axis without affecting the shape of the curves. The admissible ranges for the parameters are 0 ≤ m < 1 and C ≥ 0. A notch-insensitive laminate is characterized by a large d0 in comparison to R. This corresponds to m → 1 and C → 0. Figure 13.7 shows notched strength vs. hole radius for two quasi-isotropic carbon/epoxy laminates with [±45/0/90]s and [90/0/±45]s lay-ups and the magnitudes of the corresponding fitting parameters m and C determined as outlined in Section 13.3. FIGURE 13.4 Notched strength data and predictions based on the average stress criterion for a notched [02/±45]s carbon/epoxy laminate [4]. TX001_ch13_Frame Page 173 Saturday, September 21, 2002 5:07 AM © 2003 by CRC Press LLC