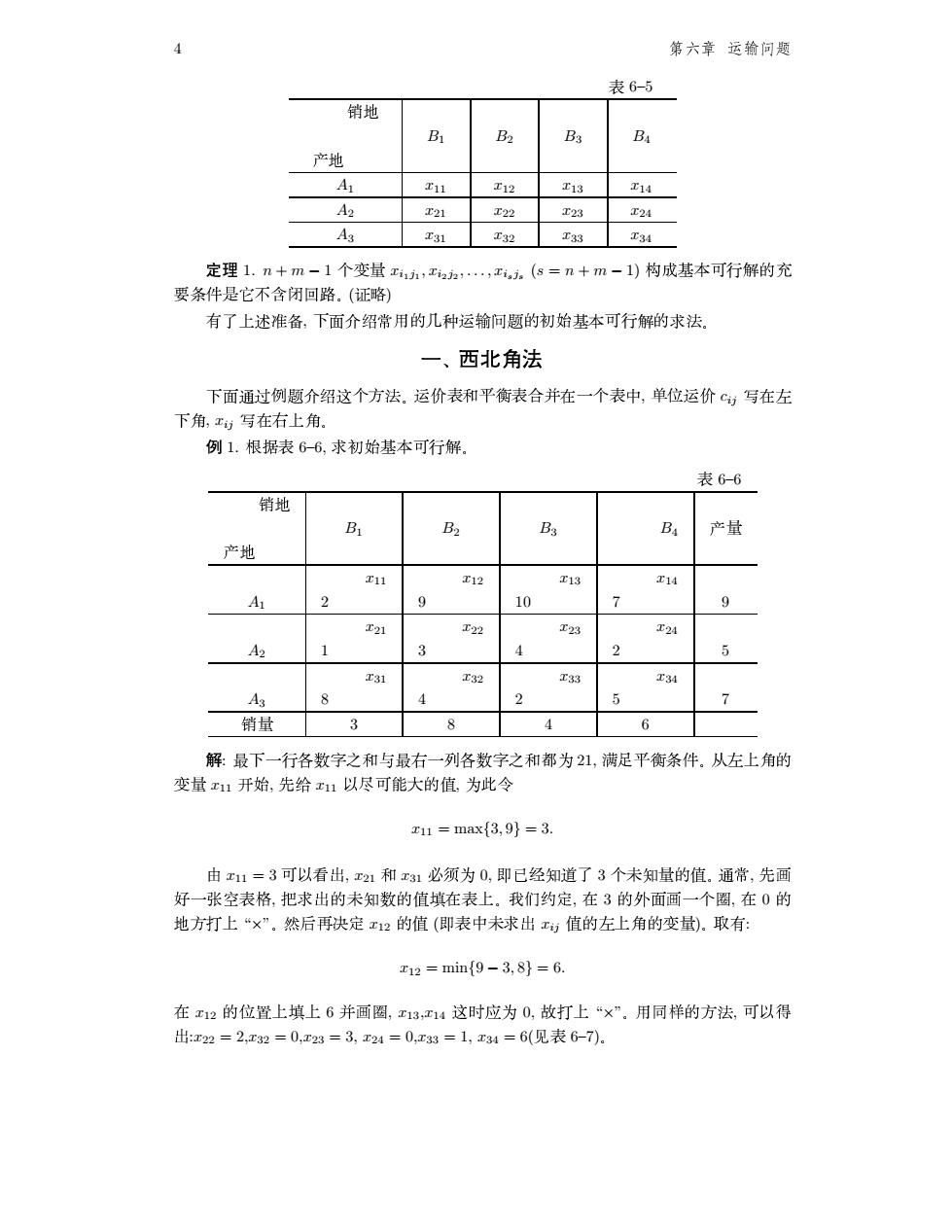
第六章运输问题 表6-5 销地 B 产地 A 11 T12 13 14 42 T21 22 T23 工24 A3 31 32 34 定理1.n十m-1个变量，，，.(s=n+m一1)构成基本可行解的充 要条件是它不含闭回路。（证略） 有了上述准备，下面介绍常用的几种运输问题的初始基本可行解的求法. 一、西北角法 下面通过例题介绍这个方法.运价表和平衡表合并在一个表中，单位运价，写在左 下角，x)写在右上角. 例1.根据表6-6，求初始基本可行解 表6-6 销地 B B B 产量 产地 12 f18 14 0 10 工22 T23 4 1 3 4 2 5 T31 工33 A3 4 销量 3 8 4 6 解最下一行各数字之和与最右一列各数字之和都为21，满足平衡条件.从左上角的 变量11开始，先给x1以尽可能大的值，为此令 x11=max{3,9}=3. 由x11=3可以看出，21和x31必须为0，即已经知道了3个未知量的值.通常，先画 好一张空表格，把求出的未知数的值填在表上。我们约定，在3的外面画一个圈，在0的 地方打上“×”.然后再决定12的值（即表中未求出值的左上角的变量）.取有： 12=mim9-3,8}=6. 在x12的位置上填上6并画圈，x1314这时应为0，故打上“×”.用同样的方法，可以得 出：z22=2,T32=0,23=324=0,33=1,x34=6(见表6-7). 4 ❶✑❷❁❸❺❹✡❻✑❼❁❽ ⑦ 6–5 ✵✡✲ B1 B2 B3 B4 ✱✡✲ A1 x11 x12 x13 x14 A2 x21 x22 x23 x24 A3 x31 x32 x33 x34 ❇✁❞ 1. n + m − 1 ✰✁✘✹ xi1j1 , xi2j2 , . . . , xisjs (s = n + m − 1) Þ⑥õ✡ã③➄ Ù ✘✁❡ ✤✓✃❢➢✡û✕ ▲✝▼✥◆✛ (✸✁❢) ✒ ➝✡➐✁❵✁✜✁❣, ➊ ➑✡å✡æ✡➟✾✡✘✁❤✩✙✡✚✍✡✎✘✡ö✡÷õ✡ã③➄ Ù ✘❂Ø ✛ ✐❦❥♠❧❦♥❦♦❦♣ ➊ ➑✁q✁r➶✎✡å✡æ✡✜✰❈✡Ø✛ ✙✡♥⑦ ✺❣✡❤✡⑦❍✁❳✟✓ ✰✡⑦ ✏ , ❵✡❛✙✡♥ cij s✟✁t ➊✁✉, xij s✟➆ ➐ ✉ ✛ ❙ 1. ✈✁✇⑦ 6–6, ❂ ö✡÷õ✡ã③➄ Ù✡✛ ⑦ 6–6 ✵✡✲ B1 B2 B3 B4 ✱✹ ✱✡✲ x11 x12 x13 x14 A1 2 9 10 7 9 x21 x22 x23 x24 A2 1 3 4 2 5 x31 x32 x33 x34 A3 8 4 2 5 7 ✵✹ 3 8 4 6 ✈ : ❆➊✓✡➄✁①✡✇✁②✁③✡✺✁❩✡❆✡➆✡✓⑤①✡✇✁②✁③✡✺➸ ❴ 21, ➔✡→✡❣✡❤✁✓✃✡✛ ✭t✡➐✉✘ ✘ ✹ x11 ④÷, ✎Ñ x11 ④✁⑤✡③s✁⑥✘✁⑦, ❴❥✁⑧ x11 = max{3, 9} = 3. ❦ x11 = 3 ③↔④↔➌⑧, x21 ✺ x31 ❐↔❒❴ 0, ✐➦✿➞ ❀✰⑨➝ 3 ✰ ➅↔❀↔✹↔✘✰⑦✛✴q↔➟, ✎✰❲ ✮✬✓✡⑩✡❶⑦✡❷, ✧✬❂⑧✬✘✬➅✬❀✬✇✬✘✡⑦✡❸✟⑦➐✬✛ ➎✬➏✡✑❄ , ✟ 3 ✘✬❝➑✡❲✓ ✰✡❹, ✟ 0 ✘ ✲❈✁❺➐ “×”✛ Ó ø✁❻✖❄ x12 ✘✁⑦ (✐⑦ ✏➅ ❂ ⑧ xij ⑦✡✘t✡➐✉✘✘ ✹)✛❽❼✒: x12 = min{9 − 3, 8} = 6. ✟ x12 ✘❛✡❾➐❸ ➐ 6 ❳ ❲❹ , x13,x14 ✜✬❰✸✬❴ 0, ❿✡❺➐ “×”✛ ✾✬②✠ ✘✬❈✬Ø, ③✬④ ✯ ⑧:x22 = 2,x32 = 0,x23 = 3, x24 = 0,x33 = 1, x34 = 6(➀⑦ 6–7)✛