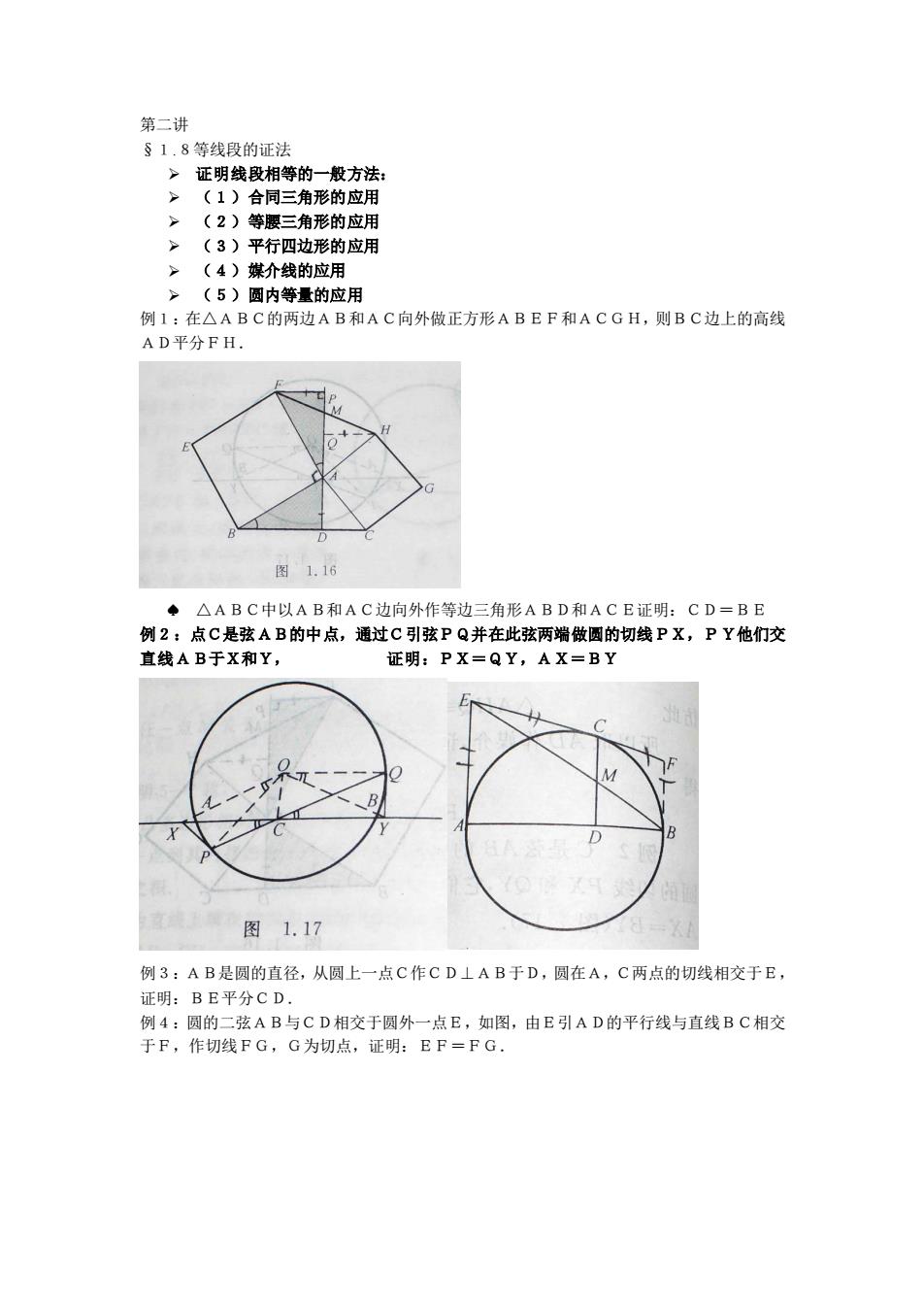
第二讲 §1.8等线段的证法 >证明线段相等的一般方法 (1)合同三角形的应用 (2)等腰三角形的应用 >（3)平行四边形的应用 (4)煤介线的应用 B和AC向外做正方形ABEF和ACGH,则BC边上的高线 AD平分FH. 图1.16 ◆△ABC中以AB和AC边向外作等边三角形ABD和ACE证明：CD=BE 例2：点C是弦AB的中点，通过C引弦PQ并在此弦两端做圆的切线PX,PY他们交 直线AB于X和Y, 证明：PX=QY,AX=BY 图1.17 例3：AB是圆的直径，从圆上一点C作CD上AB于D,圆在A,C两点的切线相交于E 证明：BE平分CD. 例4：圆的二弦AB与CD相交于圆外一点E,如图，由E引AD的平行线与直线BC相交 于F,作切线FG,G为切点，证明：EF=FG, 第二讲 §１.８等线段的证法 ➢ 证明线段相等的一般方法： ➢ （１）合同三角形的应用 ➢ （２）等腰三角形的应用 ➢ （３）平行四边形的应用 ➢ （４）媒介线的应用 ➢ （５）圆内等量的应用 例１：在△ＡＢＣ的两边ＡＢ和ＡＣ向外做正方形ＡＢＥＦ和ＡＣＧＨ，则ＢＣ边上的高线 ＡＤ平分ＦＨ． △ＡＢＣ中以ＡＢ和ＡＣ边向外作等边三角形ＡＢＤ和ＡＣＥ证明：ＣＤ＝ＢＥ 例２：点Ｃ是弦ＡＢ的中点，通过Ｃ引弦ＰＱ并在此弦两端做圆的切线ＰＸ，ＰＹ他们交 直线ＡＢ于Ｘ和Ｙ， 证明：ＰＸ＝ＱＹ，ＡＸ＝ＢＹ 例３：ＡＢ是圆的直径，从圆上一点Ｃ作ＣＤ⊥ＡＢ于Ｄ，圆在Ａ，Ｃ两点的切线相交于Ｅ， 证明：ＢＥ平分ＣＤ． 例４：圆的二弦ＡＢ与ＣＤ相交于圆外一点Ｅ，如图，由Ｅ引ＡＤ的平行线与直线ＢＣ相交 于Ｆ，作切线ＦＧ，Ｇ为切点，证明：ＥＦ＝ＦＧ．