第二讲 §1.8等线段的证法 >证明线段相等的一般方法 (1)合同三角形的应用 (2)等腰三角形的应用 >(3)平行四边形的应用 (4)煤介线的应用 B和AC向外做正方形ABEF和ACGH,则BC边上的高线 AD平分FH. 图1.16 ◆△ABC中以AB和AC边向外作等边三角形ABD和ACE证明:CD=BE 例2:点C是弦AB的中点,通过C引弦PQ并在此弦两端做圆的切线PX,PY他们交 直线AB于X和Y, 证明:PX=QY,AX=BY 图1.17 例3:AB是圆的直径,从圆上一点C作CD上AB于D,圆在A,C两点的切线相交于E 证明:BE平分CD. 例4:圆的二弦AB与CD相交于圆外一点E,如图,由E引AD的平行线与直线BC相交 于F,作切线FG,G为切点,证明:EF=FG
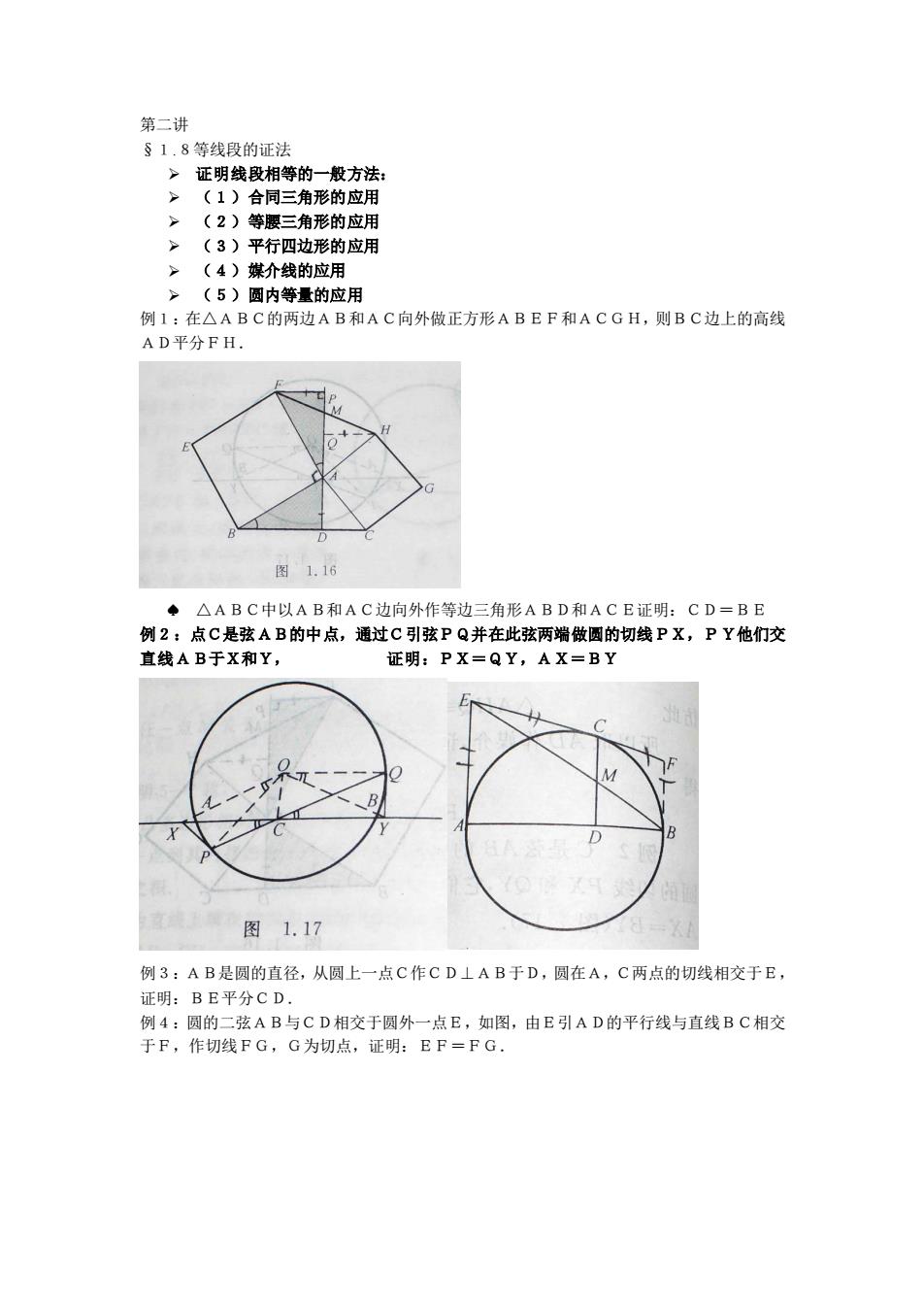
第二讲 §1.8等线段的证法 ➢ 证明线段相等的一般方法: ➢ (1)合同三角形的应用 ➢ (2)等腰三角形的应用 ➢ (3)平行四边形的应用 ➢ (4)媒介线的应用 ➢ (5)圆内等量的应用 例1:在△ABC的两边AB和AC向外做正方形ABEF和ACGH,则BC边上的高线 AD平分FH. △ABC中以AB和AC边向外作等边三角形ABD和ACE证明:CD=BE 例2:点C是弦AB的中点,通过C引弦PQ并在此弦两端做圆的切线PX,PY他们交 直线AB于X和Y, 证明:PX=QY,AX=BY 例3:AB是圆的直径,从圆上一点C作CD⊥AB于D,圆在A,C两点的切线相交于E, 证明:BE平分CD. 例4:圆的二弦AB与CD相交于圆外一点E,如图,由E引AD的平行线与直线BC相交 于F,作切线FG,G为切点,证明:EF=FG.

§1.9等角的证法 ,证明角相等,主要有以下途径 (1)合回 三角形的应用 (2)等腰三角形的应用: >(3)平行线的应用: >(4)媒介角的应用: >(5)三角形中内角与外角的关系: (6)圆心角 角,弦切角的关系 (7)相似形的应用. 例1:设AD,BE,CF是△ABC的三条高线,则△DEF称为△ABC的垂足三角形.证 明这些高线平分垂足三角形的内角或外角, 图1.21 图1.22 例2:从圆O外一点P引切线PC,PD,通过弦CD的中点M任作一弦AB求证:PO 平分∠APB 例3:二圆外切于P,一圆在其上一点C的切线交另一圆于A,B求证:PC是∠APB 的外角平分线。 例4:从圆心O向已知直线I作垂线OM,通过垂足M任作两条直线AB和CD,交圆于A, B,C,D.求证:AD,BC交直线I之点P,Q与M等距. 蝴蝶定理来由 蝴蝶定理最先是作为一个征求证明的问题,刊载于1815年的一份通俗杂志《里十日记》上 由于其几何图形形象奇特、貌似蝴螺 ,便以此命名。蝴蝶定理出现过许多优美奇特的解法 其中最早的,应首推霍纳在1815年所给出的证法。至于初等数学的证法,在国外资料中 一般都认为是由一位中学教师斯特温首先提出的,它给予出的是面积证法。 ·至于初等数学的证法,在国外资料中,一般都认为是由一位中学教师斯特温首先提 出的,它给予出的是面积证法,其中应用了面积公式:S=1/2 BCSINA。1985年,在 河南省《数学教师》创刊号上,杜锡录同志以《平面几何中的名题及其妙解》为题, 载文向国内介绍蝴蝶定理 从此蝴螺定理在神州大地到处传开 §1.10和差倍分的证法和定值问题 >证明和差倍分问题的常用定理: >(1)三角形两边中点的连线等于第三边的一半:
§1.9等角的证法 ➢ 证明角相等,主要有以下途径: ➢ (1)合同三角形的应用; ➢ (2)等腰三角形的应用; ➢ (3)平行线的应用; ➢ (4)媒介角的应用; ➢ (5)三角形中内角与外角的关系; ➢ (6)圆心角,圆周角,弦切角的关系; ➢ (7)相似形的应用. 例1:设AD,BE,CF是△ABC的三条高线,则△DEF称为△ABC的垂足三角形.证 明这些高线平分垂足三角形的内角或外角. 例2:从圆O外一点P引切线PC,PD.通过弦CD的中点M任作一弦AB 求证:PO 平分∠APB. 例3:二圆外切于P,一圆在其上一点C的切线交另一圆于A,B 求证:PC是∠APB 的外角平分线. 例4:从圆心O向已知直线 l 作垂线 OM,通过垂足 M 任作两条直线 AB 和 CD,交圆于 A, B,C,D.求证:AD,BC 交直线 l 之点 P,Q 与 M 等距. 蝴蝶定理来由 : 蝴蝶定理最先是作为一个征求证明的问题,刊载于 1815 年的一份通俗杂志《男士日记》上。 由于其几何图形形象奇特、貌似蝴蝶,便以此命名。蝴蝶定理出现过许多优美奇特的解法, 其中最早的,应首推霍纳在 1815 年所给出的证法。至于初等数学的证法,在国外资料中, 一般都认为是由一位中学教师斯特温首先提出的,它给予出的是面积证法。 • 至于初等数学的证法,在国外资料中,一般都认为是由一位中学教师斯特温首先提 出的,它给予出的是面积证法,其中应用了面积公式:S=1/2 BCSINA。1985 年,在 河南省《数学教师》创刊号上,杜锡录同志以《平面几何中的名题及其妙解》为题, 载文向国内介绍蝴蝶定理,从此蝴蝶定理在神州大地到处传开。 §1.10 和差倍分的证法和定值问题 ➢ 证明和差倍分问题的常用定理: ➢ (1)三角形两边中点的连线等于第三边的一半;

》(2)梯形两腰中点的连线等于两底和的一半: >(3)平行四边形的对角线互相平分,菱形的角被对角线平分 (4)直角 三角形中若有 一个锐角头 130 则斜边是30°角对边的2倍 (5)直角三角形斜边中点距三顶点等远 (6)三角形一外角等于不相邻二内角之和等等 例1:等边三角形外接圆周上任一点到三顶点的连线中,最长的等于其余两线的和 例2:三角形任一顶点到垂心的距离,二倍于外心到对边的距离. 例3:设E为正方形ABCD中CD边的中点, F是CE的中点,则∠DAE=∠BF 证明几何问题方法可灵活机动 ·运用几何方法证明代数问题 ·例1: 设00,b>0,a+b=1求证 5<a+与+b+5s2 例3:证明直角三角形中,弦的立方大于勾股的立方和. 例4:在△ABC的高线AD上任取一点P,设有两条直线BP与AC相交于M,两直线C P与AB相交于N,证明AD平分∠MDN或其外角】 例5:设P为△ABC外接圆周上任一点,则PA2+PB2+PC2=2AE
➢ (2)梯形两腰中点的连线等于两底和的一半; ➢ (3)平行四边形的对角线互相平分,菱形的角被对角线平分; ➢ (4)直角三角形中若有一个锐角为 30°,则斜边是 30°角对边的2倍; ➢ (5)直角三角形斜边中点距三顶点等远; ➢ (6)三角形一外角等于不相邻二内角之和等等 例1:等边三角形外接圆周上任一点到三顶点的连线中,最长的等于其余两线的和 例2:三角形任一顶点到垂心的距离,二倍于外心到对边的距离. 例3:设E为正方形ABCD中CD边的中点, F是CE的中点,则∠DAE= 证明几何问题方法可灵活机动 • 运用几何方法证明代数问题 • 例1: 例2: 例3:证明直角三角形中,弦的立方大于勾股的立方和. 例4:在△ABC的高线AD上任取一点P,设有两条直线BP与AC相交于M,两直线C P与AB相交于N,证明AD平分∠MDN或其外角. 例5:设P为△ABC外接圆周上任一点,则PA2+PB2+PC2=2AB 1 2 BAF 2 2 2 2 2 2 2 2 0 ,0 , ( ) ( ) ( ) ( ) 2 2 a l b l a b l a b a l b l a l b l + + − + + + − + − + − 设 求证下面不等式 0, 0, 1. 1 1 2 2 2 2 a b a b a b + = + + + 已知 求证