
初等数论 主讲:xiehm
初等数论 主讲:xiehm

序言篇 数论是研究整数性质的一门很古 老的数学分支,其初等部分是以整数 的整除理论、同余理论为中心的,包 括整除性、不定方程、同余式、连分 数、素数(即整数)分布以及数论函 数等内容,统称初等数论 (elementary number theory)
序言篇 数论是研究整数性质的一门很古 老的数学分支,其初等部分是以整数 的整除理论、同余理论为中心的,包 括整除性、不定方程、同余式、连分 数、素数(即整数)分布以及数论函 数等内容,统称初等数论 (elementary number theory)

初等数论的大部分内容早在古希 腊欧几里德的《几何原本》中就已出 现。欧几里得证明了素数有无穷多个, 他还给出求两个自然数的最大公约数 的方法,即所谓欧几里得算法。我国 古代在数论方面亦有杰出之贡献,现 在一般数论书中的“中国剩余定理” 正是我国古代《孙子算经》中的下卷 第26题,我国称之为“孙子定理
初等数论的大部分内容早在古希 腊欧几里德的《 几何原本》中就已出 现。欧几里得证明了素数有无穷多个, 他还给出求两个自然数的最大公约数 的方法, 即所谓欧几里得算法。我国 古代在数论方面亦有杰出之贡献,现 在一般数论书中的“中国剩余定理” 正是我国古代《孙子算经》中的下卷 第26题,我国称之为“孙子定理”

近代初等数论的发展得益于费 马、欧拉、拉格朗日、勒让德和 高斯等人的工作。1801年,高斯的 《算术探究》是数论的划时代杰作。 高斯还提出:“数学是科学之王, 数论是数学之王”。可见高斯对数 论的高度评价
近代初等数论的发展得益于费 马、欧拉、拉格朗日、勒让德和 高斯等人的工作。1801年,高斯的 《算术探究》是数论的划时代杰作。 高斯还提出:“数学是科学之王, 数论是数学之王”。可见高斯对数 论的高度评价

欧几里德 高斯
欧几里德 高斯

欧拉 费马
欧拉 费马

拉格朗日 毕达格拉斯
拉格朗日 毕达格拉斯

数论的分支 由于自20世纪以来引进了抽象代 数和高等分析的巧妙工具,数论得到 进一步的发展,从而开阔了新的研究 领域,出现了代数数论、解析数论、 几何数论等新分支。而且近年来初等 数论在计算器科学、组合数学、密码 学、代数编码、计算方法等领域内更 得到了广泛的应用,无疑同时促进着 数论的发展
数论的分支 由于自20世纪以来引进了抽象代 数和高等分析的巧妙工具,数论得到 进一步的发展,从而开阔了新的研究 领域,出现了代数数论、解析数论、 几何数论等新分支。而且近年来初等 数论在计算器科学、组合数学、密码 学、代数编码、计算方法等领域内更 得到了广泛的应用,无疑同时促进着 数论的发展
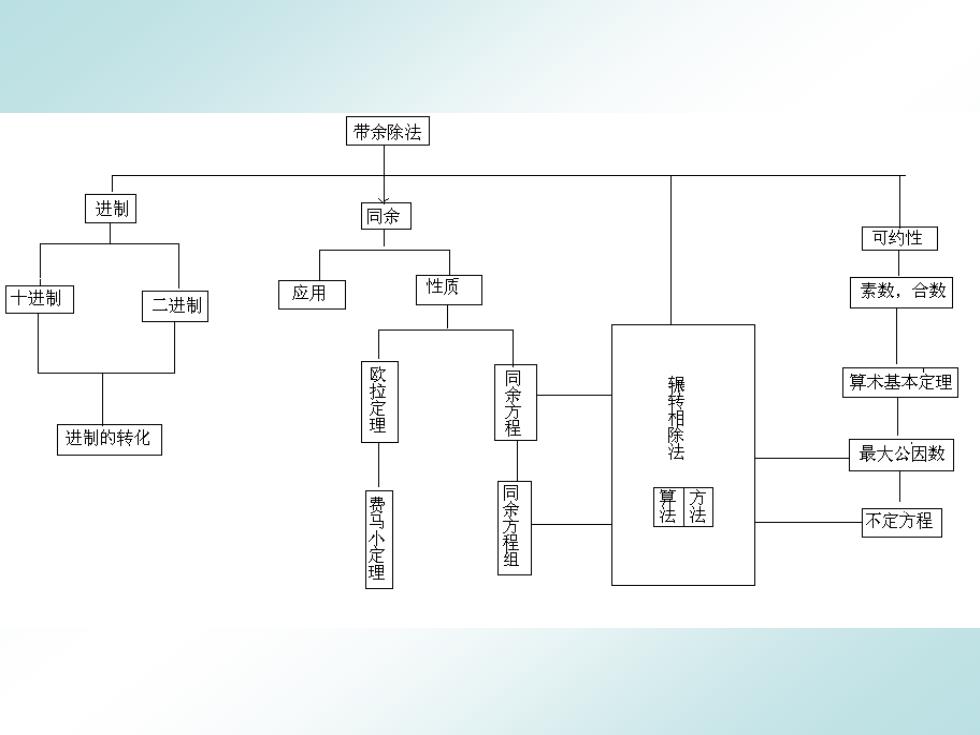
带余除法 进制 同余 可约性 十进制 性质 二进制 应用 素数,合数 欧拉定理 同余方程 算术基本定理 进制的转化 辗转相除法 最大公因数 费马小定理 同余方程组 不定方程
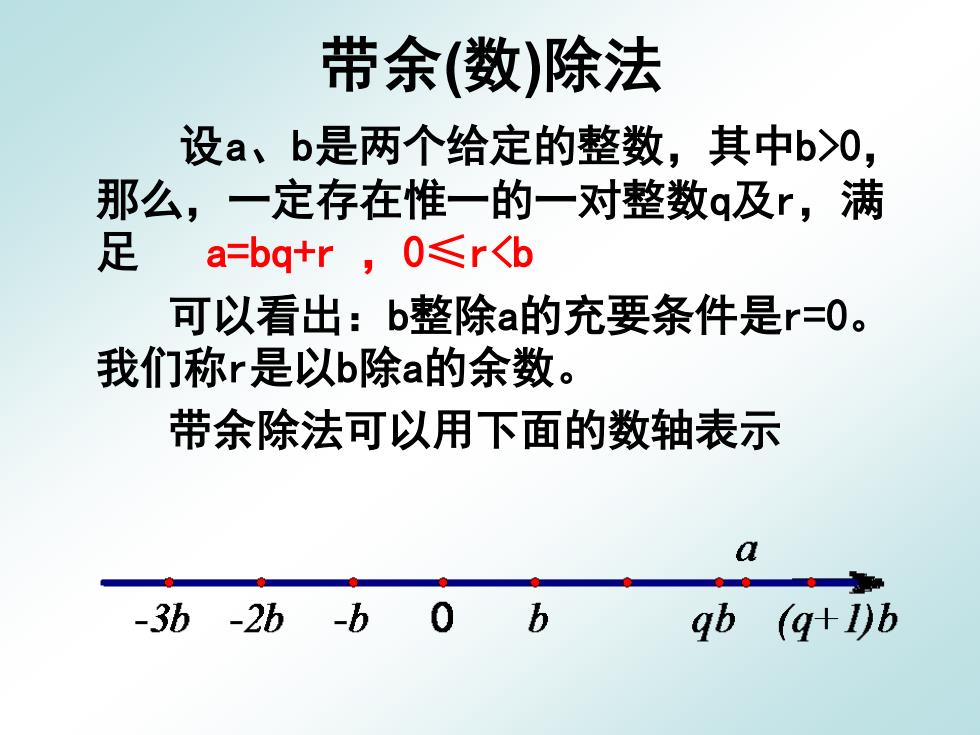
带余(数)除法 设a、b是两个给定的整数,其中b>0, 那么,一定存在惟一的一对整数q及「,满 足 a=bq+r,0≤r<b 可以看出:b整除a的充要条件是r=0。 我们称r是以b除a的余数。 带余除法可以用下面的数轴表示 a -3b-2b-b 0 b gb (q+1)b
带余(数)除法 设a、b是两个给定的整数,其中b>0, 那么,一定存在惟一的一对整数q及r,满 足 a=bq+r ,0≤r<b 可以看出:b整除a的充要条件是r=0。 我们称r是以b除a的余数。 带余除法可以用下面的数轴表示