
如何选择数学复习课的例题 北京昌平孟婷 摘要:新课标下学生的数学能力不仅在于对知识的掌握,更在于能否应用知识自觉解 决实际问题,复习课必须精心设计练习题,使知识的应用更具综合性和灵活性,看他能否运 用数学知识数学思维去解决实际问题以及形成学习新知识的能力和适合社会发展的需要。 因此,例题选择要有代表性,典型性,示范性,综合性,灵活性、发展性,有利于培养学生 的实践能力和创新意识。 关键词:复习课精选例题巩固双基提高能力 复习课:难各课难上课,学生收效不明显。那么,上好一堂数学复习课的关键之一就是 例题的选择,通过一道代表性例题的复习,讲解和发挥,把某些基本概念和基本方法阐述得 一清二楚,这样既强化“双基”又提高了能力。因此所选的例题应具备有:典型性、延伸性 创造性和启发性。本文通过以下几方面来展示例题选择的关键所在。 一、一题多解有利于培养学生思维的广阀性。 对于同一道题,从不同的角度去分析研究,可能会得到不同的启示,从而引出多种 不同的解法。 在教学中,不失时机地通过引导学生进行“一题多解”的训练,通过广泛的联 想,使我们的思维触角伸向不同的方向,不同的层次,这样不仅能巩固所学知识,而且能较 好地培养学生思维的广阔性。 3-c08x 解法一:(有界性法) cosx-3-y 30-y) 1+y 。koss1 1+y ,解之得: 25y5 。即所求函数的值城为。号习 解法二:(分离变量法)
如何选择数学复习课的例题 北京昌平 孟 婷 摘 要:新课标下学生的数学能力不仅在于对知识的掌握,更在于能否应用知识自觉解 决实际问题,复习课必须精心设计练习题,使知识的应用更具综合性和灵活性,看他能否运 用数学知识、数学思维去解决实际问题,以及形成学习新知识的能力和适合社会发展的需要。 因此,例题选择要有代表性,典型性,示范性,综合性,灵活性、发展性,有利于培养学生 的实践能力和创新意识。 关键词:复习课 精选例题 巩固双基 提高能力 复习课:难备课难上课,学生收效不明显。那么,上好一堂数学复习课的关键之一就是 例题的选择,通过一道代表性例题的复习,讲解和发挥,把某些基本概念和基本方法阐述得 一清二楚,这样既强化“双基”又提高了能力。因此所选的例题应具备有:典型性、延伸性、 创造性和启发性。本文通过以下几方面来展示例题选择的关键所在。 一、一题多解有利于培养学生思维的广阔性. 对于同一道题,从不同的角度去分析研究,可能会得到不同的启示,从而引出多种 不同的解法。在教学中,不失时机地通过引导学生进行“一题多解”的训练,通过广泛的联 想,使我们的思维触角伸向不同的方向,不同的层次,这样不仅能巩固所学知识,而且能较 好地培养学生思维的广阔性。 例 1:求函数 的值域。 解法一:(有界性法) 由 ,得: 。 , ,解之得: 。即所求函数的值域为: 解法二:(分离变量法)

6 得:y=-1+3+c08xkos水s1,253+csx54 解法三:(判别式法) 1-tan2 2+4tan2 C03x■ y■ I+tan2 4+2tan2 。2+42 ,得: “艺,即4+2云,可化为: ②+y-20,由别别式可得:4-②y-9y-沙20,解得:y52 即所求西数的值线为。号,习 解法四:(导数法) 短a六司上器y 6 。:所求函数的值城为:宁 由前四种解题方法中,通过以题带面复习了“函数的定义域、值域、性质”、“三角 函数的有界性”等知识,加深了知识间的沟通,同时培养了学生解的转化策略,体现了函 数与方程的思想在数学中的作用。接若引导学生运用转化及数形结合的思想方法解题。 3-c08x。3-c0sx 解法五:由+c0co为 《结合斜率公式),则y可看成是由定点 AB,3)与动点B(c0xc0s连线的斜率。显然,B点在线段y-x≤D上,如图】 所示,可得:
由 ,得: , , , 。即所求函数的值域为: 解法三:(判别式法) 设 ,由 ,得: ,即 ,可化为: ,由判别式可得: ,解得: , 即所求函数的值域为: 。 解法四:(导数法) 先证明函数 在 上是增函数。故: ,即: 。 所求函数的值域为: 由前四种解题方法中,通过以题带面复习了“函数的定义域、值域、性质”、“三角 函数的有界性”等知识,加深了知识间的沟通,同时培养了学生解题的转化策略,体现了函 数与方程的思想在数学中的作用。接着引导学生运用转化及数形结合的思想方法解题。 解法五:由 (结合斜率公式),则 可看成是由定点 与动点 连线的斜率。显然, 点在线段 上,如图 1 所示,可得:

k仙=2ka,=2.sys2 即所求隔数的值城为。号,习 类似解法,可电y各+0闲0则y可看成是功 C3+c0sx3-c0s刀与原点连线的斜率,而点C在线段x+y=6(2≤y≤4上,故由图 2可得e2o,号y52 即所求函数的值线为。宁习 力点 >C2 2 4 图2 k=必丛 因为函数的解析式是分式,因此完全可用解析几何中的斜率公式~方求解。可 见转化思想在数学中的地位非常重要,同时要求学生认直比较四种解法的利整与依据,然后 启发学生:一道好题能激发人的兴趣,引导人的思想,启迪人的思维,在平时的学习中应养 成探素不同的方法解题的习惯,这样才能更好地提高解题的能力。 二、例题选邦要结合重点内容与概念。 对于一些知识要重点加以研究,进行纵向和横向的联想。俗话说“伤其十指,不如断其 一指”,在每一章每一节的学习中,必须积累一些典型题目并经常对其进行研究,培养解题 意识,以便能起到以一顶十的作用。 如在复习立体几何的有关性质与概念时。应让学生熟悉典型模型(重点:正方体、四面 体)的相关结论及论证过程这样可大大提高解题效率 如正方体AC中
。 即所求函数的值域为: 类 似 解 法 : 可 由 , 则 可看成是动点 与原点连线的斜率。而点 在线段 上,故由图 2 可得: , ,即所求函数的值域为: 因为函数的解析式是分式,因此完全可用解析几何中的斜率公式 求解。可 见转化思想在数学中的地位非常重要,同时要求学生认真比较四种解法的利弊与依据,然后 启发学生:一道好题能激发人的兴趣,引导人的思想,启迪人的思维,在平时的学习中应养 成探索不同的方法解题的习惯,这样才能更好地提高解题的能力。 二、例题选择要结合重点内容与概念。 对于一些知识要重点加以研究,进行纵向和横向的联想。俗话说“伤其十指,不如断其 一指”,在每一章每一节的学习中,必须积累一些典型题目并经常对其进行研究,培养解题 意识,以便能起到以一顶十的作用。 如在复习立体几何的有关性质与概念时。应让学生熟悉典型模型(重点:正方体、四面 体)的相关结论及论证过程这样可大大提高解题效率. 如正方体 A1C 中
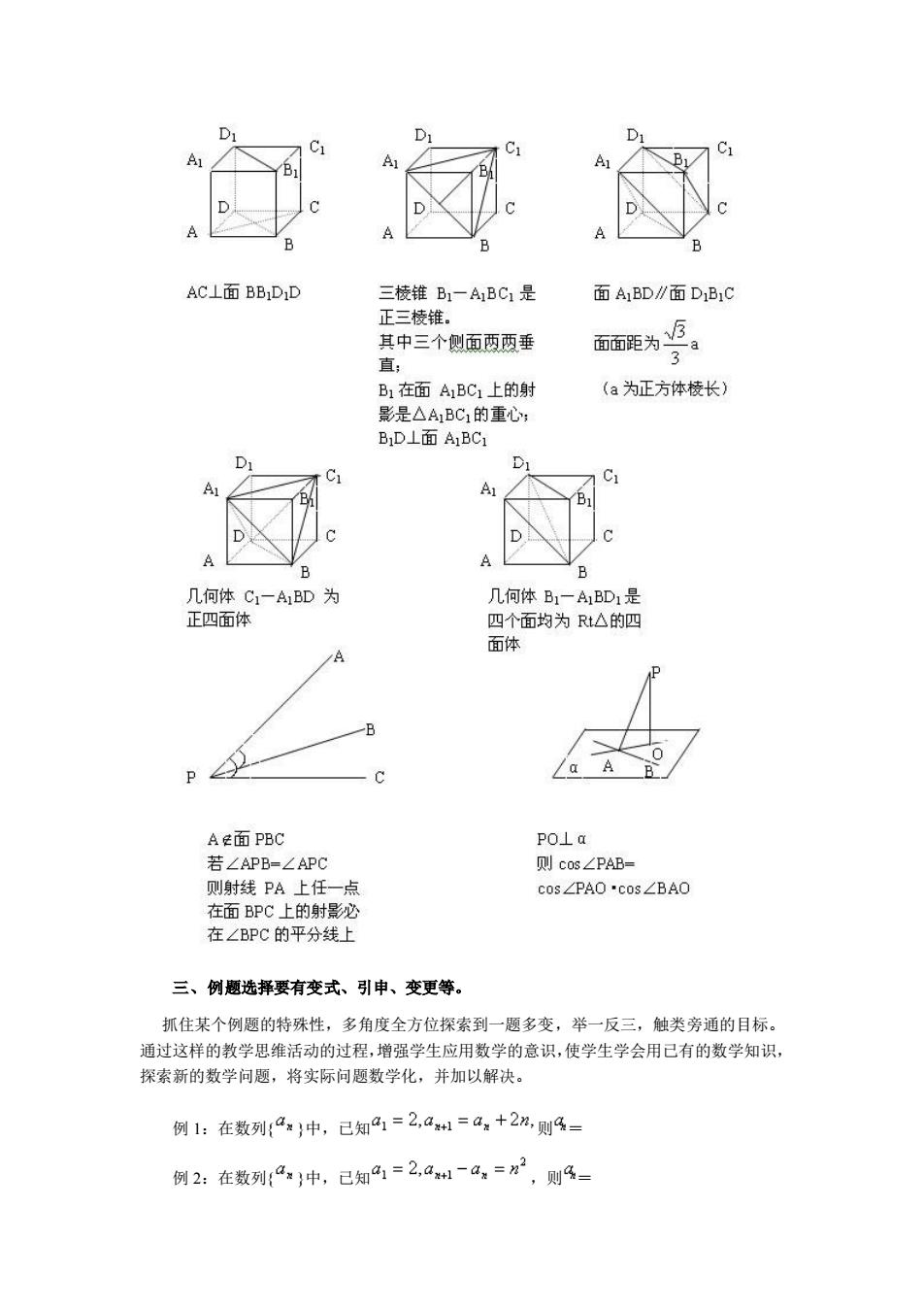
☒ AC⊥面BBDD 三棱锥B1一ABC是 面A1BD∥面DB1C 其中三个侧面两两垂 直: 爽为, B1在面A1BC1上的射 (a为正方体棱长) 影是△A1BC1的重心, BD⊥面A1BC 几何体 C一A1BD为 几何体B1一ABD是 正四面体 四个面均为Rt△的四 面体 6 aA C POLa 则c0g∠PAB= 则射线PA上任一点 c03∠PA0·C0s∠BA0 在面BPC上的射影必 在∠BPC的平分线上 三、例题选择要有变式、引申、变更等。 抓住某个例题的特殊性,多角度全方位探索到一题多变,举一反三,触类旁通的日标 通过这样的教学思维活动的过程,增强学生应用数学的意识,使学生学会用己有的数学知识 探索新的数学问题,将实际问题数学化,并加以解决。 例1:在数列4中,已知41=2,a1=a,+2m,则4 例2:在数列4中,已知4=2,a1-4=分,则4三
三、例题选择要有变式、引申、变更等。 抓住某个例题的特殊性,多角度全方位探索到一题多变,举一反三,触类旁通的目标。 通过这样的教学思维活动的过程,增强学生应用数学的意识,使学生学会用已有的数学知识, 探索新的数学问题,将实际问题数学化,并加以解决。 例 1:在数列{ }中,已知 则 = 例 2:在数列{ }中,已知 ,则 =

例3在数电,已知吗=2,-,g: ,则4 例4:在数列4a)中,已知41=2,a1-a=2,则a1= 1 例5:在数列4)冲,已知4,=2,01-4,=a+可,则4= 例6:在数列(4中,已知41=2,a1-a=8:2”,则a= 此题组是按照常数,一次函数,二次函数,指数函数,对数函数的顺序思考的它可以 使学生掌握所有运用叠加法4,=4+(a,-4)+色-4)++(a,-a1)解决数列求 通项公式的问愿. 四、要重视数形结合,注意应用。 数形结合是研究数学问思常用的一种思想方法,是转化的数学思想的重要体现。是解决 函数问题的最简洁最重要的手段。它主要是借助形的直观性米阐明数之间的联系,其次是借 助于数的结确性来阐明形的某些属性。其实质是将抽象的数学语言与直观的图像结合起来 关键是代数问题与图形之间的相互转化。 例1:如果奇函数f(x)在区间[3,7]上是增函数且最小值是5,那么f(x)的[-7,-3]上是 A.增函数且最小值为一5 B.增函数且最大值为一5 C.减函数且最小值为-5 D.减函数且最大值为一5 例2.若方程1g(-x2+3x一)=1g(3-x)在x∈(0,3)内有唯一解,求实数m的取值范 围 3-x>0 -x>0 【解】原方程变形为之+3x-m=3-x 即:x-2)2=1-m 设曲线y1=(x-2)2,x∈(0,3)和直线y2-1一m,图像如图所示
例 3:在数列{ }中,已知 , ,则 = 例 4:在数列{ }中,已知 , 则 = 例 5:在数列{ }中,已知 , ,则 = 例 6:在数列{ }中,已知 , 则 = 此题组是按照常数,一次函数,二次函数,指数函数,对数函数的顺序思考的.它可以 使学生掌握所有运用叠加法: = )解决数列求 通项公式的问题. 四、要重视数形结合,注意应用。 数形结合是研究数学问题常用的一种思想方法,是转化的数学思想的重要体现。是解决 函数问题的最简洁最重要的手段。它主要是借助形的直观性来阐明数之间的联系,其次是借 助于数的精确性来阐明形的某些属性。其实质是将抽象的数学语言与直观的图像结合起来, 关键是代数问题与图形之间的相互转化。 例 1:如果奇函数 f(x)在区间[3,7]上是增函数且最小值是 5,那么 f(x)的[-7,-3]上是 _。 A.增函数且最小值为-5 B.增函数且最大值为-5 C.减函数且最小值为-5 D.减函数且最大值为-5 例 2. 若方程 lg(-x +3x-m)=lg(3-x)在 x∈(0,3)内有唯一解,求实数 m 的取值范 围。 【解】 原方程变形为 即: 设曲线 y =(x-2) , x∈(0,3)和直线 y =1-m,图像如图所示

由图可知:①当1一m=0时,有唯一解,m=1: ②当1≤1-K4时,有唯 一解,即-30,0.2匀<0则方程的根落在区间()。 A.(1,1.25)B.(125,1.5)C.(1.5,2)D.不能确定 例2:函数1(闭=2x2-2的零点所在的区间是(). A(-3,-2) B(-1,0) C(2,3)D(4,5) 例3:方程x=3-x的实数解落在的区间是() A[0,1B.[1,2]c[2,3D[3.4] 例4:函数fx)=3ax-2a+1在区间(-l,1)上存在一个零点,求a的取值范围 通过解析该题组,让学生对方程根的概念与根的性质有了了解,并能运用二分法逼近根 的范围。 大、数学知识的综合运用。 综合题主要涉及代数,几何等不同学科的多方面内容,所应用的知识和技巧比较多,有 助于所学的数学知识融会贯通,起到复习提高的作用,有助于培养学生综合运用的能力。 例如图,平面内有三个向量OAO丽.0元,其中A与O丽的夹角为120°,O员与0C 的夹角为30°,且可iH丽1,元=25,若0元=0A+4O丽(2,4e∈R),则 元+4的值为一 解析:是+4=6
由图可知:① 当 1-m=0 时,有唯一解,m=1; ②当 1≤1-m<4 时,有唯 一解,即-3<m≤0, ∴ m=1 或-3<m≤0 此题借助于图像直观解决,简单明了。此题也可用代数方法来讨论方程的解的情况,还 可用分离参数法来求(也注意结合图像分析只一个 x 值)。 五、由浅入深,逐步提高。 选择的例题要求,由浅入深、由易到难,由表及里使学生在掌握基础知识的同时,提高 解题能力,也可以培养学生的自信,勇于实践探索的精神。 例 1:设 , 用二分法求方程 内近似解的过程 中, 计算得到 , , 则方程的根落在区间( ). A.(1,1.25) B.(1.25,1.5) C.(1.5,2) D.不能确定 例 2: 函数 的零点所在的区间是( ). A (-3,-2) B(-1,0) C(2,3) D(4,5) 例 3: 方程 的实数解落在的区间是( ) 例 4:函数 f(x)=3ax-2a+1 在区间(-1,1)上存在一个零点,求 a 的取值范围 通过解析该题组,让学生对方程根的概念与根的性质有了了解,并能运用二分法逼近根 的范围。 六、数学知识的综合运用。 综合题主要涉及代数,几何等不同学科的多方面内容,所应用的知识和技巧比较多,有 助于所学的数学知识融会贯通,起到复习提高的作用,有助于培养学生综合运用的能力。 例:如图,平面内有三个向量 、 、 ,其中 与 的夹角为 120°, 与 的夹角为 30°,且 , = ,若 ( ∈R),则 的值为 . 解析: .

法1:坐标法:建立平面直角坐标系,通过建立平面直角坐标系,利用三角函数的定义, 把向量运算转化为坐标运算 法2:向量法:考虑到三个向量的模已知,两两夹角也已知,所以利用向量的数量积处 理。 法3:根据向量加法的平行四边形法则.联想到向量加法的平行四边形法则,通过作图 解直角三角形获解 以上三种解法都是解答本题的基本方法,体现了数形结合,等价转化的思想方法。此 是三角、向量、解析几何的综合恩,培养了学生综合解题的能力。 选择复习课例题的同时,应选配相应的配套练习愿,让学生独力思考,独立完成,使学 生对所学的知识能深化并提高分析问题和解决问题的能力。 2011-09-29人教网
法 1:坐标法;建立平面直角坐标系, 通过建立平面直角坐标系,利用三角函数的定义, 把向量运算转化为坐标运算. 法 2:向量法;考虑到三个向量的模已知,两两夹角也已知,所以利用向量的数量积处 理. 法 3:根据向量加法的平行四边形法则.联想到向量加法的平行四边形法则,通过作图, 解直角三角形获解 以上三种解法都是解答本题的基本方法,体现了数形结合,等价转化的思想方法. 此 题是三角、向量、解析几何的综合题,培养了学生综合解题的能力。 选择复习课例题的同时,应选配相应的配套练习题,让学生独力思考,独立完成,使学 生对所学的知识能深化并提高分析问题和解决问题的能力。 2011-09-29 人教网