
·高考对数学思想和方法的要求 ·用数学思想方法指导解题
• 高考对数学思想和方法的要求 • 用数学思想方法指导解题

美国著名数学教育家波利亚说过,掌 握数学就意味着要善于解题。而当我们解 题时遇到一个新问题,总想用熟悉的题型 去“套”,这只是满足于解出来,只有对 数学思想、数学方法理解透彻及融会贯通 时,才能提出新看法、巧解法。 高考试题十分重视对于数学思 想方法的考查,特别是突出考查能 力的试题,其解答过程都蕴含着重 要的数学思想方法
美国著名数学教育家波利亚说过,掌 握数学就意味着要善于解题。而当我们解 题时遇到一个新问题,总想用熟悉的题型 去“套”,这只是满足于解出来,只有对 数学思想、数学方法理解透彻及融会贯通 时,才能提出新看法、巧解法。 高考试题十分重视对于数学思 想方法的考查,特别是突出考查能 力的试题,其解答过程都蕴含着重 要的数学思想方法

一、高考对数学思想和方法的 要求 “数学科的命题,在考查基础知识的 基础上,注重对数学思想和方法的 考查,注重对数学能力的考查,注 重展现数学的科学价值和人文价值” (《考试说明》(理科,2006年)
一、高考对数学思想和方法的 要求 “数学科的命题,在考查基础知识的 基础上,注重对数学思想和方法的 考查,注重对数学能力的考查,注 重展现数学的科学价值和人文价值” (《考试说明》(理科,2006年)

数学思想和方法,是对数学知识在更高层 次的抽象和概括,考查时必须要与数学知识 相结合,通过数学知识的考查,反映考生对 数学思想和方法的理解;要从学科整体 意义和思想价值上立意,注意通性 通法,淡化特殊技巧,有效地检测考 生对中学数学知识中所蕴涵的数学思想和方 法的掌握程度.”(《考试大纲》(理科, 2007年)
数学思想和方法,是对数学知识在更高层 次的抽象和概括,考查时必须要与数学知识 相结合,通过数学知识的考查,反映考生对 数学思想和方法的理解;要从学科整体 意义和思想价值上立意,注意通性 通法,淡化特殊技巧,有效地检测考 生对中学数学知识中所蕴涵的数学思想和方 法的掌握程度. ”(《考试大纲》(理科, 2007年)

举例子 ·代数一数量关系是根本,函数概念是核 心,重点体现函数、方程的思想,重视代 数推理。 解析几何—用代数方法解决几何问题是 其核心价值,重点体现数形结合的思想。 立体几何—将空间线面的位置关系和数 量关系转化到平面中加以研究是其重要特 点,重点体现转化思想
• 代数——数量关系是根本,函数概念是核 心,重点体现函数、方程的思想,重视代 数推理。 • 解析几何——用代数方法解决几何问题是 其核心价值,重点体现数形结合的思想。 • 立体几何——将空间线面的位置关系和数 量关系转化到平面中加以研究是其重要特 点,重点体现转化思想。 举例子
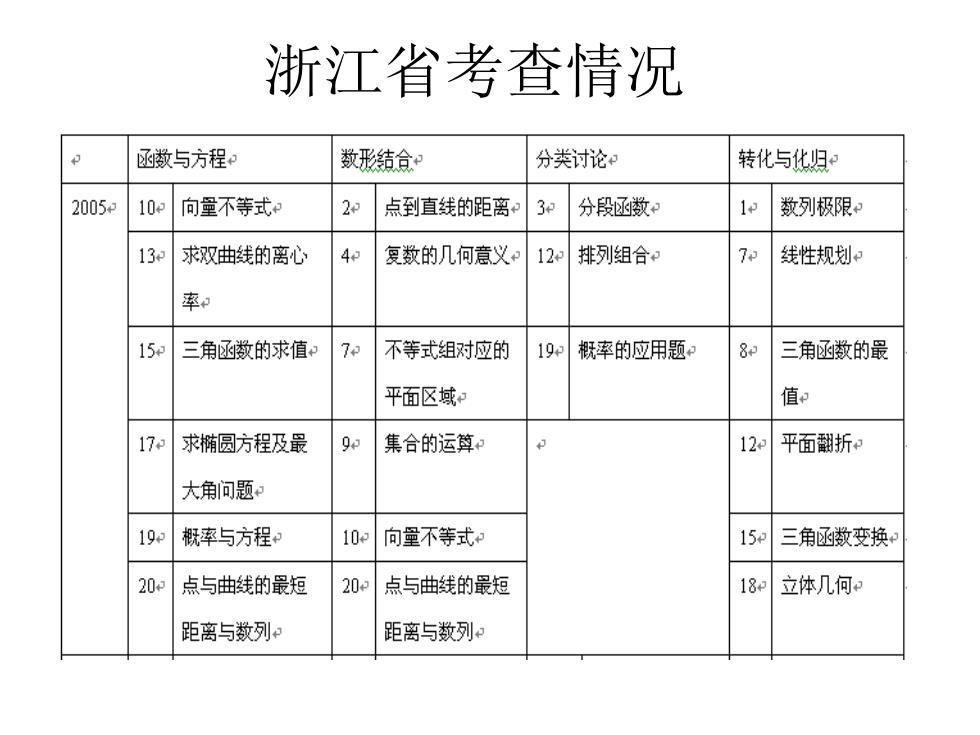
浙江省考查情况 函数与方程 数形结合 分类讨论 转化与化归 2005 10e 向量不等式 2 点到直线的距离: 3 分段还函数 1 数列极限 13 求双曲线的离心 4 复数的几何意义 120 排列组合 7 线性规划 率 15 三角函数的求值和 1e 不等式组对应的 19 概率的应用题 8e 三角函数的最 平面区域 值 170 求椭圆方程及最 集合的运算? 12 平面翻折+ 大角问题 190 概率与方程 10e 向量不等式 15 三角函数变换 20 点与曲线的最短 20日 点与曲线的最短 182 立体几何 距离与数列 距离与数列
浙江省考查情况
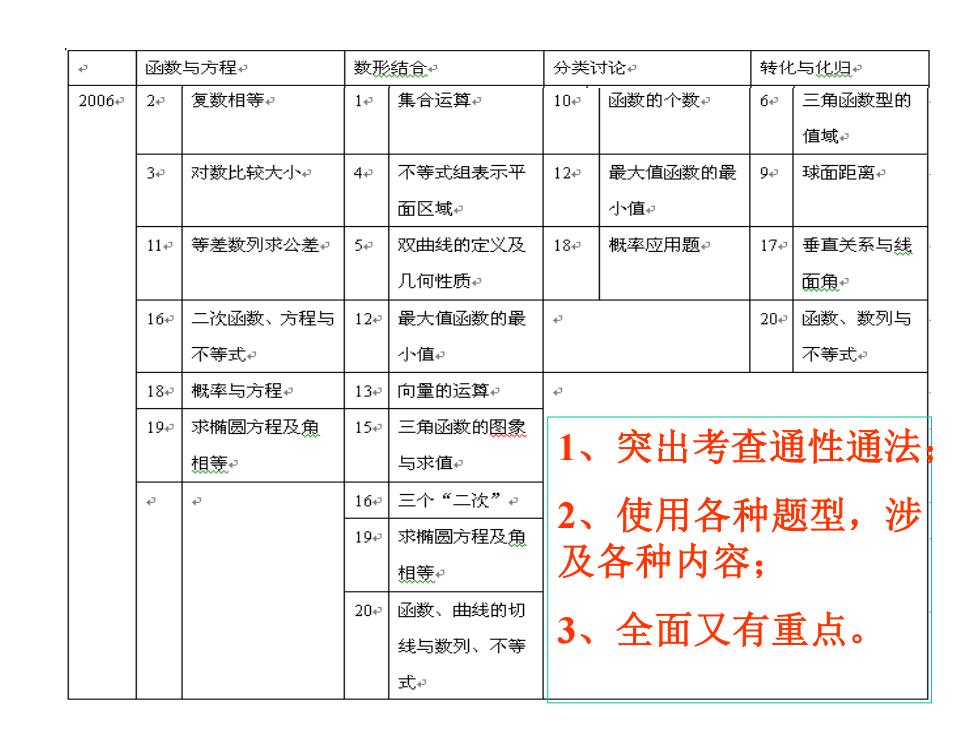
丞数与方程 数形结合 分类讨论 转化与化归 2006 20 复数相等: 1 集合运算 10 函数的个数 6 三角函数型的 值域 对数比较大小 4 不等式组表示平 12 最大值函数的最 93 球面距离 面区域和 小值和 11 等差数列求公差 5 双曲线的定义及 183 慨率应用题 173 垂直关系与线 几何性质 面角 16 二次函数、方程与 12 最大值函数的最 20 函数、数列与 不等式 小值和 不等式 18和 概率与方程 13 向量的运算 19 求椭圆方程及角 15 三角还函数的图象 1、 突出考查通性通法 相等 与求值 16 三个“二次”和 2、使用各种题型,涉 19 求椭圆方程及角 相等 及各种内容; 20 函数、曲线的切 线与数列、不等 3、全面又有重点。 式
1、突出考查通性通法; 2、使用各种题型,涉 及各种内容; 3、全面又有重点

二、考试中心对数学复习的建议 “数学思想方法较之数学基础知识有 更高的层次.具有观念性的地位,如果说 数学知识是数学内容,可用文字和符号来 记录和描述,那么数学思想方法则是数学 意识,只能领会、运用,属于思维的范畴, 用以对数学问题的认识、处理和解决, 中学数学中蕴含的数学思想方法很多, 最基本最主要的有:化归转化、类比联 想、数形结合、分类讨论、函数与方 程的思想方法等
二、考试中心对数学复习的建议 “数学思想方法较之数学基础知识有 更高的层次.具有观念性的地位,如果说 数学知识是数学内容,可用文字和符号来 记录和描述,那么数学思想方法则是数学 意识,只能领会、运用,属于思维的范畴, 用以对数学问题的认识、处理和解决. 中学数学中蕴含的数学思想方法很多, 最基本最主要的有:化归转化、类比联 想 、数形结合、 分类讨论、 函数与方 程的思想方法等

“数学思想方法与数学基本方法 常常在学习、掌握数学知识的同 时获得,与此同时又应该领会它 们在形成知识中的作用,到了复 习阶段应该对数学思想方法和数 学基本方法进行疏理、总结,逐 个认识它们的本质特征、思维程 序或者操作程序,逐步做到自觉 地、灵活地施用于所要解决的问 题
“数学思想方法与数学基本方法 常常在学习、掌握数学知识的同 时获得,与此同时又应该领会它 们在形成知识中的作用,到了复 习阶段应该对数学思想方法和数 学基本方法进行疏理、总结,逐 个认识它们的本质特征、思维程 序或者操作程序,逐步做到自觉 地、灵活地施用于所要解决的问 题

近几年来,高考的每一道数学 试题几乎都考虑到数学思想方法或 数学基本方法的运用,目的也是加 强这些方面的考查.同样,这些高考 试题也成为检验数学知识,同时又 是检验数学思想方法的良好素材, 复习时可以有意识地加以运用.” 感 感想 感悟 魁
近几年来,高考的每一道数学 试题几乎都考虑到数学思想方法或 数学基本方法的运用,目的也是加 强这些方面的考查.同样,这些高考 试题也成为检验数学知识,同时又 是检验数学思想方法的良好素材, 复习时可以有意识地加以运用.” 感 知 感 想 感 悟 创 造