
第一讲 关于初等几何 ◆ 在中学数学载材中占据重要的地位 ■是历次数学课程改革的重点 ■中小学几何课程的历史发展 ■几乎占据了“三大能力”中的两大能力:逻辑推理能力,空间想象能力 第一章证愿法。初等几何变换。 度量与计算 §1.1引言 ■初等几何研究的对象是多方面的: ■初等几何研究有利于大家从更为一般,更为概括而连续的角度分析现行中小学数学 教材中的初等几何.可以举例说明 (欧氏几何命题,绝对几何命题 §1,2关于数学证明 ■数学需要证明,证明后的结论需要实践的检验。 ■严格的数学证明有助于抓住事物的本质,上升到一般理论,从而使数学具有高度的 抽象性和广泛的应用性 ·直观与推理 ·关于命题证明 ■命恩由两部分组成:前提(假设)与结论,数学上的命题常写成假言命题的形式 ■命题不一定是真的,即不一定成立,真命题称为定理. ■数学证明:由假设经过推理得出结论.推理的每一步都要求言必有据 §1,3命题的四种变化 ■换位:把一个命题的前提和结论互换地位,前提变为结论,结论变为前提, 。换质:把命题的两部分同时加以否定,地位保持不变. ■设原命题为若P则Q”,则换位以后为“若Q则P”,此命趣称为原命题的逆命题: 换质以后为若非P则非Q”出命题称为原命题的否命题 ■经过换位与换质,有一个命题可得到四个命题: (1)原命 题:若P则Q,P一Q: ■ (2)逆命题:若Q则P,Q一P: ■(3)否命题:若P则Q,PQ: ■(4)逆否命题:若Q则P,Q一P ■例1: (1)原命题:正方形的对角线互相直平分 (真) (2)逆命题:对角线互相垂直平分的四边形是正方形.(假) (3)否命题:不是正方形的四边形对角线不能互相垂直平分.(假) (4)逆否命题:对角线不互相垂直平分的四边形不是正方形.(真) 四种命题的关系图示如下:
第一讲 关于初等几何 ◼ 在中学数学教材中占据重要的地位 ◼ 是历次数学课程改革的重点 ◼ 中小学几何课程的历史发展 ◼ 几乎占据了“三大能力”中的两大能力:逻辑推理能力,空间想象能力 第一章 证题法.初等几何变换. 度量与计算 §1.1 引言 ◼ 初等几何研究的对象是多方面的; ◼ 初等几何研究有利于大家从更为一般,更为概括而连续的角度分析现行中小学数学 教材中的初等几何.可以举例说明 ◼ (欧氏几何命题,绝对几何命题) §1.2 关于数学证明 ◼ 数学需要证明,证明后的结论需要实践的检验. ◼ 严格的数学证明有助于抓住事物的本质,上升到一般理论,从而使数学具有高度的 抽象性和广泛的应用性. ◼ 直观与推理 ◼ 关于命题证明 ◼ 命题由两部分组成:前提(假设)与结论.数学上的命题常写成假言命题的形式 ◼ 命题不一定是真的,即不一定成立,真命题称为定理. ◼ 数学证明:由假设经过推理得出结论.推理的每一步都要求言必有据. §1.3 命题的四种变化 ◼ 换位:把一个命题的前提和结论互换地位,前提变为结论,结论变为前提. ◼ 换质:把命题的两部分同时加以否定,地位保持不变. ◼ 设原命题为“若P则Q”,则换位以后为“若Q则P”,此命题称为原命题的逆命题; 换质以后为“若非P则非Q”.此命题称为原命题的否命题. ◼ 经过换位与换质,有一个命题可得到四个命题: ◼ (1)原命题:若P则Q,P→Q; ◼ (2)逆命题:若Q则P,Q→P; ◼ (3)否命题:若P则Q,P→Q; ◼ (4)逆否命题:若Q则P,Q→P. ◼ 例1: (1)原命题:正方形的对角线互相直平分.(真) (2)逆命题:对角线互相垂直平分的四边形是正方形.(假) (3)否命题:不是正方形的四边形对角线不能互相垂直平分.(假) (4)逆否命题:对角线不互相垂直平分的四边形不是正方形.(真) 四种命题的关系图示如下:

§1.3.1四种命愿的真假关系 ■若原命题为真,则他的逆命或否命题未必为真 个定理的逆命题或 否命题必须通过判断才能确定真债 ·互为逆否的两个命题,真则同真,假则同假. ■综上所述,原命题与其逆否命题是等价的:原命题的逆命题与原命题的否命题是等 价的. 813,2充分条件。必要条件.充要条件 铅 在定理P Q(若P则Q)中,条件P成为性质Q的充分条件:Q称为P 的必要 ■若原命题与逆命题同时成立:P一Q,Q→P,则P是Q的充分和必要条件:Q 也是P的充分和必要条件.即P与Q互为充要条件, 关于必要和充分的意义,可概括如下 必要:无它必不行,有它未必行: ■ (2)充分:有它必行,无它未必不行: ■(3)充要:有它必行,无它必不行. 例如:对角线互垂是菱形的必要条件而不是充分条件:菱形的充要条件? 81,33证明命题要蓝防出错 个题是否成立 ·若要否定一个错误的命题,只要找到一个反例即可。 。如要否定“若四边形四边相等,则为正方形”只要举菱形为例即可:要否定“若两多边 形的对应边相等,则必相似”,只要举菱形与正方形即可. ■命题:有一双对边相等和一双对角相等的四边形是平行四边形. ■设四边形ABCD中,AD=BC /A=/C,求证ABCD是平行四边形 §1.4逆命题证法 证明逆命题,常用下列方法: (1)直接证明逆命题:将原命题的证明过程反其道而行之, 举例说明: ■定理:角平分线上的点到角两边的距离相等(原命题) 逆命题:到角两边距离相等的点在角的平分线上 ■(2)证明与逆命题等效的否命题 ■如上例, ■不在角平分线上的点到角两边的距离不相等 ■(3)利用原命题本身证明逆命题 ■例:两直线被一直线所截,若同位角相等,则此两直线平行(原命题) ■逆命题:两平行直线被一直线所截,则同位角相等. §1.5直接证法与间接证法 1)直接证法:由命题的假设出发,根据定义,公理,定理进行一系列正面的推 理,最后得出命题的结论,此证明方法称为直接证法. ■(2)对于不能直接证明的命题,我们往往证明它的等效命题,这种证明方法称为 间接证法
§1.3.1四种命题的真假关系 ◼ 若原命题为真,则他的逆命题或否命题未必为真. ◼ 一个定理的逆命题或否命题必须通过判断才能确定真假. ◼ 互为逆否的两个命题,真则同真,假则同假. ◼ 综上所述,原命题与其逆否命题是等价的;原命题的逆命题与原命题的否命题是等 价的. §1.3.2充分条件.必要条件.充要条件 ◼ 一般地,在定理P→Q(若P则Q)中,条件P成为性质Q的充分条件;Q称为P 的必要条件. ◼ 若原命题与逆命题同时成立: P→Q,Q→P,则P是Q的充分和必要条件; Q 也是P的充分和必要条件.即P与Q互为充要条件. 关于必要和充分的意义,可概括如下: ◼ (1)必要:无它必不行,有它未必行; ◼ (2)充分:有它必行,无它未必不行; ◼ (3)充要:有它必行,无它必不行. 例如:对角线互垂是菱形的必要条件而不是充分条件;菱形的充要条件? §1.3.3证明命题要谨防出错 ◼ 关键要会判断一个命题是否成立. ◼ 若要否定一个错误的命题,只要找到一个反例即可. ◼ 如要否定“若四边形四边相等,则为正方形”只要举菱形为例即可;要否定“若两多边 形的对应边相等,则必相似”,只要举菱形与正方形即可. ◼ 命题:有一双对边相等和一双对角相等的四边形是平行四边形. ◼ 设四边形ABCD中,AD=BC, ∠A=∠C,求证ABCD是平行四边形 §1.4逆命题证法 证明逆命题,常用下列方法: ◼ (1)直接证明逆命题:将原命题的证明过程反其道而行之. 举例说明: ◼ 定理:角平分线上的点到角两边的距离相等(原命题) 逆命题:到角两边距离相等的点在角的平分线上 ◼ (2)证明与逆命题等效的否命题 ◼ 如上例,其否命题为: ◼ 不在角平分线上的点到角两边的距离不相等 ◼ (3)利用原命题本身证明逆命题 ◼ 例:两直线被一直线所截,若同位角相等,则此两直线平行(原命题) ◼ 逆命题:两平行直线被一直线所截,则同位角相等. §1.5直接证法与间接证法 ◼ (1)直接证法:由命题的假设出发,根据定义,公理,定理进行一系列正面的推 理,最后得出命题的结论,此证明方法称为直接证法. ◼ (2)对于不能直接证明的命题,我们往往证明它的等效命题,这种证明方法称为 间接证法.

■间接证法有反证法与同一法 ①反证法 由否定结论的正确性出发,根据假设,定义,公理,定理进行一系列正 确的推理 最后得出一个与命题的假设或某个公理,定理或自相子盾的结果,表明 结论的反面不能成立,从而可以肯定原结论的正确性. ■利用反证法,当结论的反面只有一款时,否定了这一款便完成了证明,这种反证法 叫归谬法: ■当结论的反面有多款时,必须驳倒其中每一款,这种反证法称谓穷举法 ■②同一法:若欲证某图形具有某种性质而又不易直接证明时,有时可以作出具有所 有性质的图形,然后证明所作的图形与所给的某图形就是同一个,把他们等同起来, 这种证明方法称为同一法, 各种证题方法的关系如下: 1,5,1间接证法举例 例, 证明:圆内不是直径的两弦不能互相平分 例2 ■证明:两内角平分线相等的三角形是等腰三角形. ■此例由莱莫斯于1840年给出,几何学家斯坦纳首先给出证明,由于它的难度, 人们常将该命题称为斯坦纳一莱莫斯定理。前苏联的在1980年 12 上将其作为问题征解,使它涉及到世界各地,据有关资料介绍,关于它的不 证法已达60多科 。穷举法案例 ■例3证明:直角三角形斜边上的中线等于斜边的一半 设直角三角形ABC,M是斜边AC的中点求证:AM=BM=CM ■分段式命题:在一个命题中, 如果假设和结论有相同的款数,且既是穷举的又是互 斥的,这样的命题叫做分段式命题. ■引申定理:分段式定理的逆定理一定成立. 例4同一法应用举例 ■以正方形ABCD的一边CD为底向形内做等腰三角形△ECD,使其两底角都是 15·则△ABE是等边三角形 81,6综合法与分析法 (1)综合法:由命题的假设入手,由因导果,通过一系列的正确推理,逐步靠近 目标,最终得出正确结论。 ■例1.如图:平行四边形ABCD外接于平行四边形BFGH则其对角线AC,B D,EG,HF共点. 分析法证明举例
◼ 间接证法有反证法与同一法 ◼ ①反证法:由否定结论的正确性出发,根据假设,定义,公理,定理进行一系列正 确的推理,最后得出一个与命题的假设或某个公理,定理或自相矛盾的结果,表明 结论的反面不能成立,从而可以肯定原结论的正确性. ◼ 利用反证法,当结论的反面只有一款时,否定了这一款便完成了证明,这种反证法 叫归谬法; ◼ 当结论的反面有多款时,必须驳倒其中每一款,这种反证法称谓穷举法. ◼ ②同一法:若欲证某图形具有某种性质而又不易直接证明时,有时可以作出具有所 有性质的图形,然后证明所作的图形与所给的某图形就是同一个,把他们等同起来, 这种证明方法称为同一法. 各种证题方法的关系如下: §1.5.1间接证法举例 例1: ◼ 证明:圆内不是直径的两弦不能互相平分. 例2 ◼ 证明:两内角平分线相等的三角形是等腰三角形. ◼ 此例由莱莫斯于1840年给出,几何学家斯坦纳首先给出证明,由于它的难度, 人们常将该命题称为“斯坦纳-莱莫斯”定理.前苏联的<数学教师>在1980年 12期上将其作为问题征解,使它涉及到世界各地,据有关资料介绍,关于它的不 同证法已达60多种 ◼ 穷举法案例 ◼ 例3 证明:直角三角形斜边上的中线等于斜边的一半 设直角三角形ABC,M是斜边AC的中点求证:AM=BM=CM ◼ 分段式命题:在一个命题中,如果假设和结论有相同的款数,且既是穷举的又是互 斥的,这样的命题叫做分段式命题. ◼ 引申定理:分段式定理的逆定理一定成立. 例4 同一法应用举例 ◼ 以正方形ABCD的一边CD为底向形内做等腰三角形△ECD,使其两底角都是 15°则△ABE是等边三角形. §1.6综合法与分析法 ◼ (1)综合法:由命题的假设入手,由因导果,通过一系列的正确推理,逐步靠近 目标,最终得出正确结论. ◼ 例1.如图:平行四边形ABCD外接于平行四边形EFGH则其对角线AC, B D,EG,HF共点. 分析法证明举例
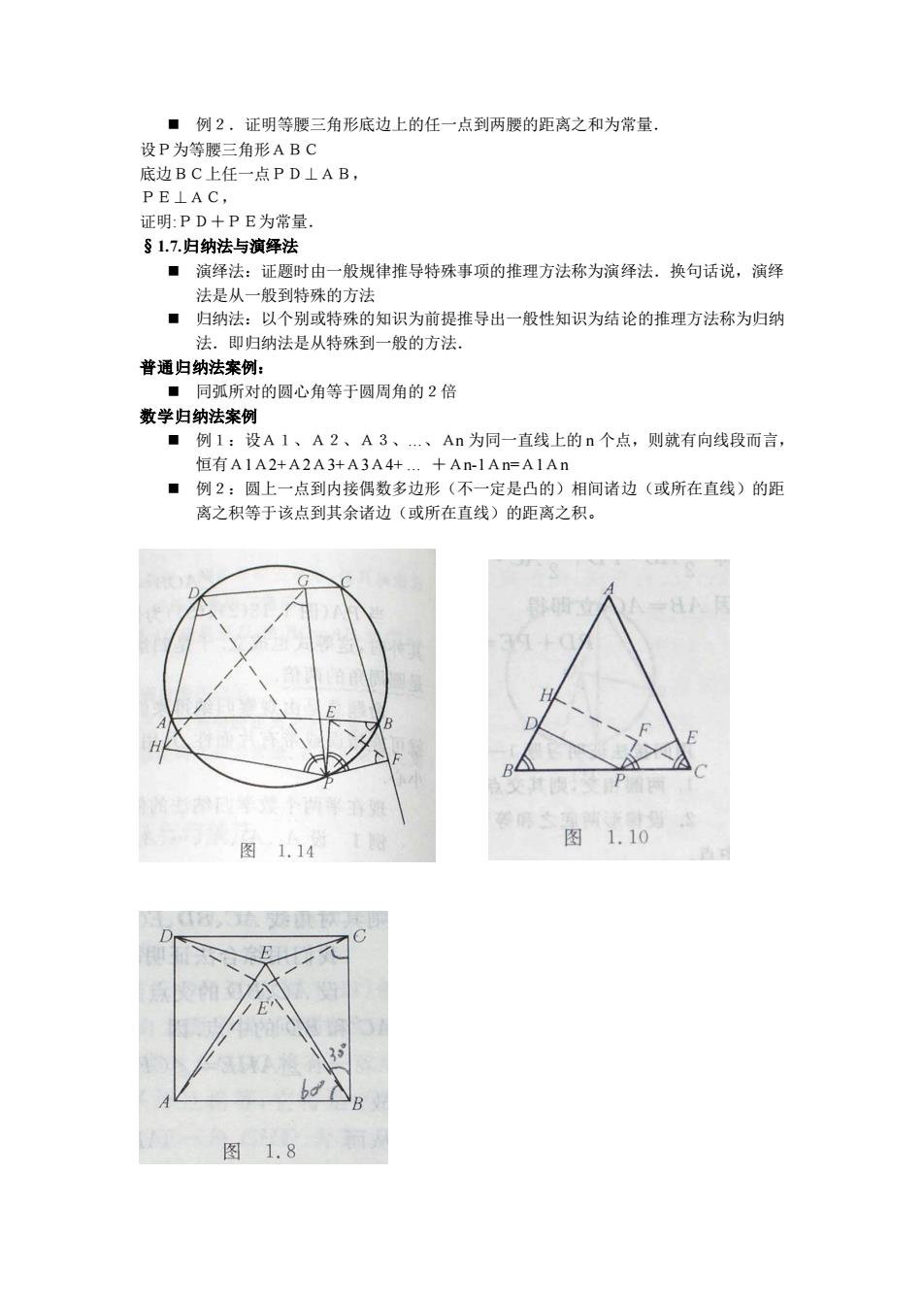
■例2.证明等腰三角形底边上的任一点到两腰的距离之和为常量. 设P为笔腰二角形ABC 证明:PD十PE为常量 §1.7.归纳法与演绎法 ■演绎法:证题时由一般规律推导特殊事项的推理方法称为演绎法,换句话说,演绎 法是从一般到特殊的方法 ■归纳法: 以个别或特殊的知识为前提推导出一般性知识为结论的推理方法称为归纳 法。即归纳法是从特殊到一般的方法。 普通归纳法案例: ■同弧所对的圆心角等于圆周角的2倍 数学归纳法案例 ■例1:设A1、A2、A3、An为同一直线上的n个点,则就有向线段而言 恒有A1A2+A2A3计A3A4++An-1An=A1An ■例2:圆上一点到内接偶数多边形(不一定是凸的)相间诸边(或所在直线)的距 离之积等于该点到其余诸边(或所在直线)的距离之积。 图1.10 图1.8
◼ 例2.证明等腰三角形底边上的任一点到两腰的距离之和为常量. 设P为等腰三角形ABC 底边BC上任一点PD⊥AB, PE⊥AC, 证明:PD+PE为常量. §1.7.归纳法与演绎法 ◼ 演绎法:证题时由一般规律推导特殊事项的推理方法称为演绎法.换句话说,演绎 法是从一般到特殊的方法 ◼ 归纳法:以个别或特殊的知识为前提推导出一般性知识为结论的推理方法称为归纳 法.即归纳法是从特殊到一般的方法. 普通归纳法案例: ◼ 同弧所对的圆心角等于圆周角的2倍 数学归纳法案例 ◼ 例1:设A1、A2、A3、.、An 为同一直线上的 n 个点,则就有向线段而言, 恒有A1A2+A2A3+A3A4+ . +An-1An=A1An ◼ 例2:圆上一点到内接偶数多边形(不一定是凸的)相间诸边(或所在直线)的距 离之积等于该点到其余诸边(或所在直线)的距离之积