
§4.6正射影,平行射影 ■2投射线,投射方向 ■从图上各点所作a的垂线称为各该点的投射线.α的法线方向称为投射方向 ■3平行射影 ·经过平行射影,点列投射成点列,线束投射成线束 ■定理1 ■设两线段合于AB∥CD,但不平行于投射方向1,则他们的平行射影合于A: '∥C'D', 并且AB:CD=AB:CD 系 ·若平行四边形不平行于投射方向,则他的平行射影仍为平行四边形, §4.6.1三垂线定理及其逆定理 ■定理2.三垂线定理 ■在斜线射影所在平面上的一直线,若垂直于这射影,则垂直于斜线本身 ■定理3三垂线定理的逆定理 ■在斜线射影所在平面上的一直线,若垂直于该射线,便也垂直于其射影 ·定理:平面上的一条斜线垂直于这平面上的定直线的充要条件是:斜线的射影垂直 于定直线. ■定理4 ■平面的一条斜线与平面上通过斜足的两条射线成等角的充要条件是:该斜线在平面
§4.6正射影,平行射影 ◼ 1射影 ◼ 给定一平面α,从一点A所引α的垂线足称为A在α上的正射影.简称射影. ◼ 2投射线,投射方向 ◼ 从图上各点所作α的垂线称为各该点的投射线. α的法线方向称为投射方向 ◼ 3平行射影 ◼ 设 是与α相交的一直线,通过一点A作直线平行于 l ,必交α于一点A’,A’ 称为A沿 l 方向在α上的平行射影 ◼ 经过平行射影,点列投射成点列,线束投射成线束 ◼ 定理1 ◼ 设两线段合于AB∥CD,但不平行于投射方向 l,则他们的平行射影合于 A’ B’ ∥C’D’, 并且 AB︰CD=A’B’ ︰C’D’ ◼ 系: ◼ 若平行四边形不平行于投射方向,则他的平行射影仍为平行四边形. §4.6.1三垂线定理及其逆定理 ◼ 定理2.三垂线定理 ◼ 在斜线射影所在平面上的一直线,若垂直于这射影,则垂直于斜线本身 ◼ 定理3 三垂线定理的逆定理 ◼ 在斜线射影所在平面上的一直线,若垂直于该射线,便也垂直于其射影. ◼ 定理:平面上的一条斜线垂直于这平面上的定直线的充要条件是:斜线的射影垂直 于定直线. ◼ 定理4 ◼ 平面的一条斜线与平面上通过斜足的两条射线成等角的充要条件是:该斜线在平面
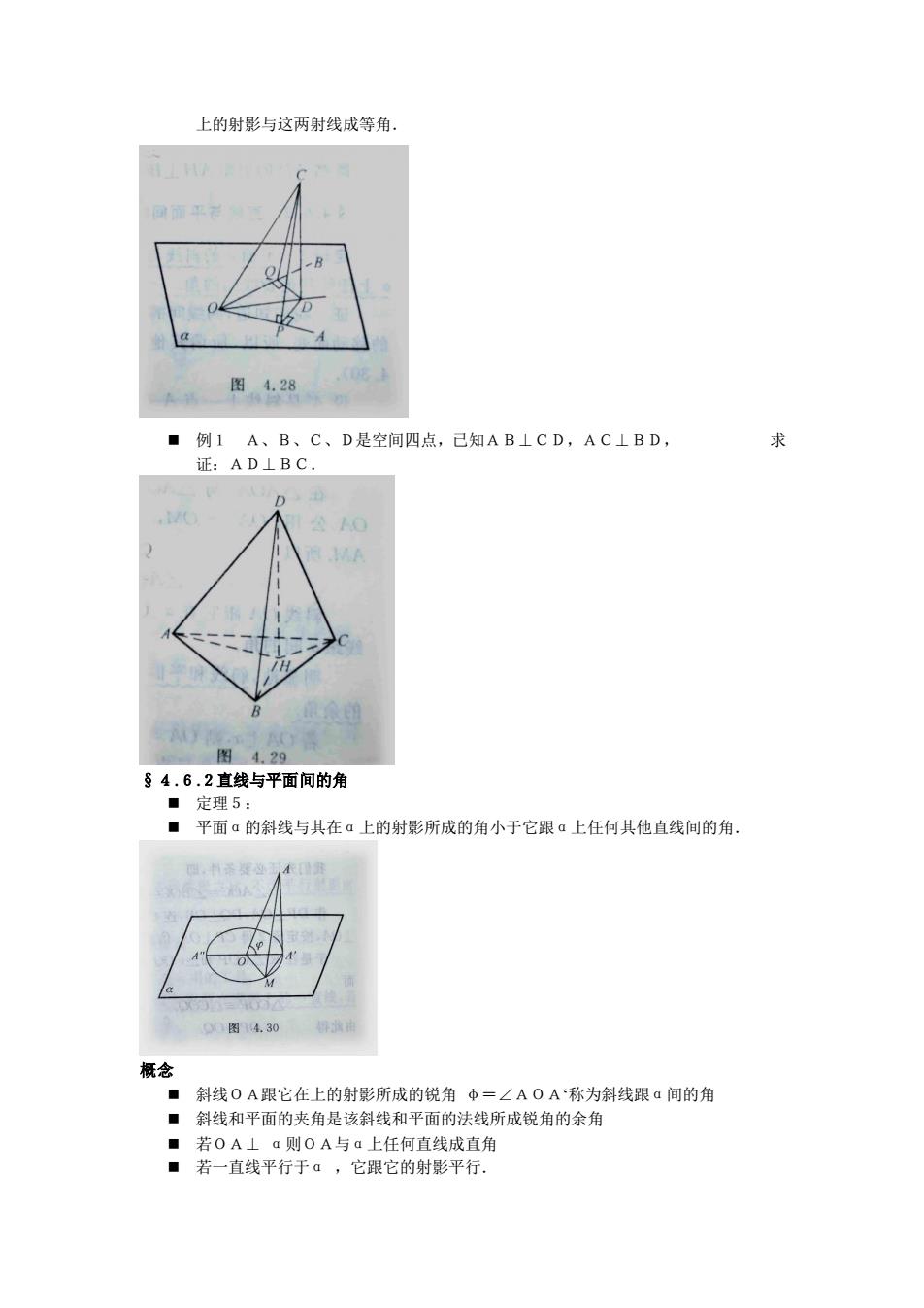
上的射影与这两射线成等角 图4.28 ■例1A、B、C、D是空间四点,己知AB⊥CD,AC⊥BD 证:AD⊥BC. 图420 §4.6.2直线与平面间的角 ■定理5 ■平面的斜线与其在上的射影所成的角小于它跟a上任何其他直线间的角 图.30 ·斜线OA跟它在上的射影所成的锐角中=∠A0A称为斜线跟a间的角 ■斜线和平面的夹角是该斜线和平面的法线所成锐角的余角 ■若0A⊥a则0A与a上任何直线成直角 。若一直线平行于ā,它跟它的射影平行
上的射影与这两射线成等角. ◼ 例1 A、B、C、D是空间四点,已知AB⊥CD,AC⊥BD, 求 证:AD⊥BC. §4.6.2直线与平面间的角 ◼ 定理5: ◼ 平面α的斜线与其在α上的射影所成的角小于它跟α上任何其他直线间的角. 概念 ◼ 斜线OA跟它在上的射影所成的锐角 φ=∠AOA‘称为斜线跟α间的角 ◼ 斜线和平面的夹角是该斜线和平面的法线所成锐角的余角 ◼ 若OA⊥ α则OA与α上任何直线成直角 ◼ 若一直线平行于α ,它跟它的射影平行.

■两平行线间的角看作零,因此平行于α的直线跟ā间的夹角为零. ■例2:斜三棱柱ABCA1B1C1的底是正三角形,其边长为a,点A1在底面 ,BC上的射影是ABC的重心G,已知侧棱跟底面的夹角为0 求这三棱柱的侧 面积和体积. §4.7 二面角,垂直平面 ■概念: ■有公共边缘的两半平面构成一面角,公共边缘是它的棱,两半平面是它的面 ■从棱上任一点P,在每一面上作垂直于棱的射线,这两射线形成二面角的平面角 将构成二面角的两面通过棱反向延展,得出它的对棱二面角 ■定理1 ■两个对棱二面角相等 。两个平面相交,组成四个二面角,两两对棱,当其中相邻的二面角相等时,两平面 称为石相垂直 ■定理2:通过已知平面的一条垂线的平面必垂直于已知平面 ■定理3 ·设两平面垂直,若一直线在其一平面,且垂直于交线,则必垂直于另一平面
◼ 两平行线间的角看作零,因此平行于α的直线跟α间的夹角为零. ◼ 例2:斜三棱柱ABCA1B1C1的底是正三角形,其边长为 a,点A1在底面 ABC上的射影是ABC的重心G,已知侧棱跟底面的夹角为θ,求这三棱柱的侧 面积和体积. §4.7 二面角,垂直平面 ◼ 概念: ◼ 有公共边缘的两半平面构成二面角,公共边缘是它的棱,两半平面是它的面. ◼ 从棱上任一点P,在每一面上作垂直于棱的射线,这两射线形成二面角的平面角. ◼ 将构成二面角的两面通过棱反向延展,得出它的对棱二面角. ◼ 定理1 ◼ 两个对棱二面角相等 ◼ 两个平面相交,组成四个二面角,两两对棱,当其中相邻的二面角相等时,两平面 称为互相垂直. ◼ 定理2:通过已知平面的一条垂线的平面必垂直于已知平面. ◼ 定理3 ◼ 设两平面垂直,若一直线在其一平面,且垂直于交线,则必垂直于另一平面.
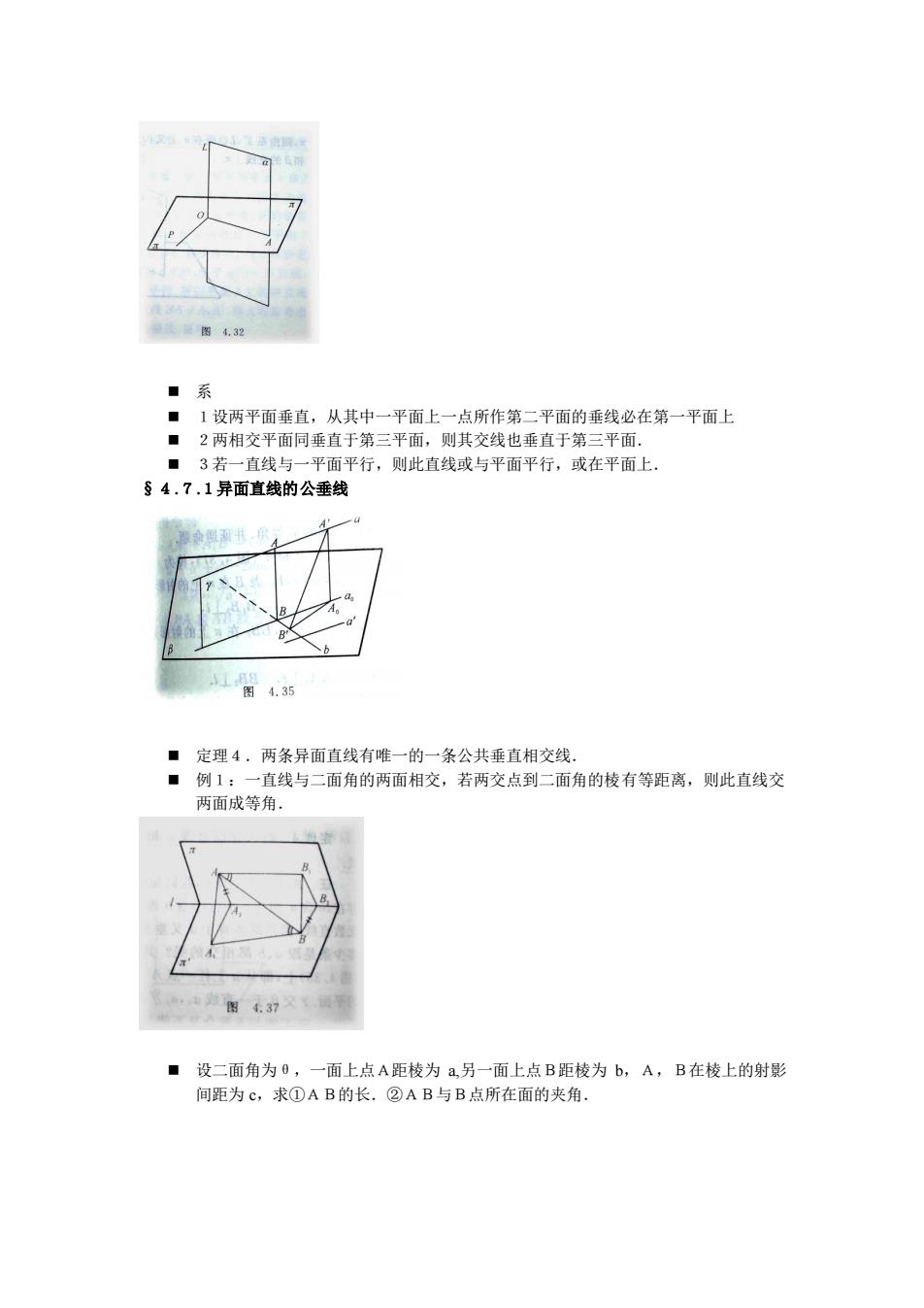
.3 ■系 1设两平面垂直,从其中一平面上一点所作第二平面的垂线必在第一平面上 ■ 2两相交平面同垂直于第三平面,则其交线也垂直于第三平面, ■3若一直线与一平面平行,则此直线或与平面平行,或在平面上. §4.7.1异面直线的公垂线 4.35 ■定理4,两条异面直线有唯一的一条公共垂直相交线。 ■例1:一直线与二面角的两面相交,若两交点到二面角的棱有等距离,则此直线交 两面成等角 图37 ■设二面角为0,一面上点A距棱为a另一面上点B距棱为b,A,B在棱上的射 间距为c,求①AB的长.②AB与B点所在面的夹角
◼ 系 ◼ 1设两平面垂直,从其中一平面上一点所作第二平面的垂线必在第一平面上 ◼ 2两相交平面同垂直于第三平面,则其交线也垂直于第三平面. ◼ 3若一直线与一平面平行,则此直线或与平面平行,或在平面上. §4.7.1异面直线的公垂线 ◼ 定理4.两条异面直线有唯一的一条公共垂直相交线. ◼ 例1:一直线与二面角的两面相交,若两交点到二面角的棱有等距离,则此直线交 两面成等角. ◼ 设二面角为θ,一面上点A距棱为 a,另一面上点B距棱为 b,A,B在棱上的射影 间距为 c,求①AB的长.②AB与B点所在面的夹角.

图4.38 54.8多面体 面内的几条射线,以及相邻两射线间的部分所组成的图 形称为多面角。组成多面角的射线称为多面角的棱。相邻两棱间的平面部分称为他 的面,相邻两棱间的角称为面角。相邻二面形成的二面角称为多面角的二面角. ■三面角的性质: ■①三面角的任何一个面角小于其他两个面角之和而大于其他两个面角之差. ■②三面角的所有面角之和小于360° ■®三面角的所有二面角之和大于180·而小于540· ·④设三面角的三个面角为a,B,Y,他们所对的二面角分别为A,B,C,则有 sina sinB siny sinA sin B sinC ■⑤设三面角的三个面角为a,B,Y,他们所对的二面角分别为A,B,C,则有 cos A=cosa-cosBcosy sin Bsiny cosB=cosB-cosacosy sinasiny cosC=cosy-cosa cosB sina sin B ■三面角全等的判定定理: ·若两个三面角的三个面角对应相等,则必相等 ■若两个三面角有两个面角及所夹的二面角对应相等,则必相等 ■若两个三面角的两个二面角及其所夹面角对应相等,则必相等. ■设两个三面角的三个二面角对应相等,则必相等. 多面角的性质 ■①多面角的任何一个面角小于其他面角之和 ②凸多面角的所有面角之和 于360 ■ ③n面角的所有面角之和大于 (n-2)180
§4.8多面体 ◼ 概念:多面角,棱,面,面角,二面角 ◼ 有公共端点并且不在同一平面内的几条射线,以及相邻两射线间的部分所组成的图 形称为多面角.组成多面角的射线称为多面角的棱.相邻两棱间的平面部分称为他 的面,相邻两棱间的角称为面角.相邻二面形成的二面角称为多面角的二面角. ◼ 三面角的性质: ◼ ①三面角的任何一个面角小于其他两个面角之和而大于其他两个面角之差. ◼ ②三面角的所有面角之和小于 360° ◼ ③三面角的所有二面角之和大于 180 ° 而小于 540 ° ◼ ④设三面角的三个面角为α,β,γ,他们所对的二面角分别为A,B,C,则有 ◼ ⑤设三面角的三个面角为α,β,γ,他们所对的二面角分别为A,B,C,则有 ◼ 三面角全等的判定定理: ◼ 若两个三面角的三个面角对应相等,则必相等. ◼ 若两个三面角有两个面角及所夹的二面角对应相等,则必相等. ◼ 若两个三面角的两个二面角及其所夹面角对应相等,则必相等. ◼ 设两个三面角的三个二面角对应相等,则必相等. 多面角的性质 ◼ ①多面角的任何一个面角小于其他面角之和. ◼ ②凸多面角的所有面角之和小于 360°. ◼ ③ n 面角的所有面角之和大于 (n-2)180 ° . sin sin sin sin sin sin A B C = = cos cos cos cos , sin sin cos cos cos cos , sin sin cos cos cos cos sin sin A B C − = − = − =