
初等代数研究 第四章方程 一、方程的历史发展及其科学价值 (方程发展简史 公元前1700年时期古埃及数学著作《兰德纸草书》记载:一个量,加上它的三,等于19,求 这个量。另一部古埃及数学著作《柏林纸草书6619》上有一个题目是“将一个面积为100的大正 方形分为两个小正方形,一个边长是另一个的子”。古巴比伦泥板书上也有类似的数学问题:“两数 互为倒数,二者之差是7,求这两个数”。 欧几里得几何《原本》中则有很多问题还要用到解二次方程 中国古代数学著作《九章算术》中有“方程”章,包含了很多关于方程的问题。“今有上禾 秉,中禾二秉,下禾一秉,实三十九斗:上禾二秉,中禾三秉,下禾一秉,实三十四斗:上禾一秉。 中禾二秉,下禾三秉,实二十六斗。问上、中、下禾实一秉各几何?”《九章算术》没有表示未知 数的符号,而是用算筹将x,y,:的系数和常数项排列成一个(长)方阵,这就是“方程”之一名称 的来源。 希腊数学家丢番图《算术》中,讨论了一次方程、二次方程和个别三次方程,还讨论了大量的 不定方程。印度数学家阿耶波多在《阿耶波多历数书》中给出了二次方程的求解方法。婆罗摩笈多 在公元628年完成的《婆罗摩笈多修正体系》一书中,也给出了一般二次方程的求根公式。 花拉子米的《代数学》一开头就指出:下列的问题,都是由根、平方与数这三样东西组成的 该书给出了六种类型一、二次 方程,分六章来叙述 13世纪的中国,在求高次方程数值解,以及解高次联立方程上有重大贡献。1247年,秦九昭 给出了一般高次方程的数值解法。李治创立的“天元术”(1248年)和朱世杰使用的“四元术”(1303 年)能够求解一大类的高次联立方程。 16世纪最伟大的数学成就是发现了三次方程和四次方程的求根公式。1515年,费罗用代数方 法求解三次方程x3+mx=n。1535年塔塔利亚宜布自己发现了形如x3+mx2=n的三次方程代 数解法。1545年,卡尔丹在《大衍术》中给出了三次方程和四次方程的解法。三次方程 x3+px=qp,9>0)的解法,实质是考虑恒等式(a-b+3ab(a-b)=a3-b3,若选取a,b, 使得3ab=p,a3-b3=g,不难解出a= 是得到a-b就是所求的x,后人称之为卡尔丹公式。 人们开始讨论一般的五次方程的解法。欧拉和拉格朗日进行了尝试,但是都以失败告终。19 世纪鲁菲尼和阿贝尔都证明了一般的五次或五次以上的方程的根不可能用方程系数的根式表出 口方程在中学数学中的地位和作用 高中阶段对方程学习有较高的要求,重点在于领会方程和函数之间的密切关系以及代数方程与 几何图形之间的密切关系。具体包含以下几方面:函数与方程,直线与方程,圆与方程,圆锥曲线 第1页共14页
初等代数研究 第1页 共14页 第四章 方程 一、方程的历史发展及其科学价值 ㈠方程发展简史 公元前 1700 年时期古埃及数学著作《兰德纸草书》记载:一个量,加上它的 7 1 ,等于 19,求 这个量。另一部古埃及数学著作《柏林纸草书 6619》上有一个题目是“将一个面积为 100 的大正 方形分为两个小正方形,一个边长是另一个的 4 3 ”。古巴比伦泥板书上也有类似的数学问题:“两数 互为倒数,二者之差是 7,求这两个数”。 欧几里得几何《原本》中则有很多问题还要用到解二次方程。 中国古代数学著作《九章算术》中有“方程”章,包含了很多关于方程的问题。“今有上禾三 秉,中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉, 中禾二秉,下禾三秉,实二十六斗。问上、中、下禾实一秉各几何?”《九章算术》没有表示未知 数的符号,而是用算筹将 x, y,z 的系数和常数项排列成一个(长)方阵,这就是“方程”之一名称 的来源。 希腊数学家丢番图《算术》中,讨论了一次方程、二次方程和个别三次方程,还讨论了大量的 不定方程。印度数学家阿耶波多在《阿耶波多历数书》中给出了二次方程的求解方法。婆罗摩笈多 在公元 628 年完成的《婆罗摩笈多修正体系》一书中,也给出了一般二次方程的求根公式。 花拉子米的《代数学》一开头就指出:下列的问题,都是由根、平方与数这三样东西组成的。 该书给出了六种类型一、二次方程,分六章来叙述。 13 世纪的中国,在求高次方程数值解,以及解高次联立方程上有重大贡献。1247 年,秦九昭 给出了一般高次方程的数值解法。李冶创立的“天元术”(1248 年)和朱世杰使用的“四元术”(1303 年)能够求解一大类的高次联立方程。 16 世纪最伟大的数学成就是发现了三次方程和四次方程的求根公式。1515 年,费罗用代数方 法求解三次方程 x + mx = n 3 。1535 年塔塔利亚宣布自己发现了形如 x + mx = n 3 2 的三次方程代 数解法。1545 年,卡尔丹在《大衍术》中给出了三次方程和四次方程的解法。三次方程 ( , 0) 3 x + px = q p q 的解法,实质是考虑恒等式 ( ) 3 3 3 a − b + 3ab(a − b) = a − b ,若选取 a,b , 使得 ab = p a − b = q 3 3 3 , ,不难解出 3 2 3 3 2 3 2 2 3 , 2 2 3 + = − + + = + q q p b q q p a ,于 是得到 a −b 就是所求的 x ,后人称之为卡尔丹公式。 人们开始讨论一般的五次方程的解法。欧拉和拉格朗日进行了尝试,但是都以失败告终。19 世纪鲁菲尼和阿贝尔都证明了一般的五次或五次以上的方程的根不可能用方程系数的根式表出。 ㈡方程在中学数学中的地位和作用 高中阶段对方程学习有较高的要求,重点在于领会方程和函数之间的密切关系以及代数方程与 几何图形之间的密切关系。具体包含以下几方面:函数与方程,直线与方程,圆与方程,圆锥曲线

初等代数研究 与方程,二阶矩阵与二元一次方程组、一阶线性差分方程、参数方程等等。 白方程的科学价值 自学教材《中学代数研究》P62-63 二、方程的定义 ()方程的几种定义 目前中学数学教科书中通用的方程定义是:含有未知数的等式。但是,形如 sin2x+cos2x=1,(x+12=x2+2x+1之类的等式难以界定。 给出一个可以取代的定义:方程是为了求未知数,在未知数和已知数之间建立的一种等式关系。 好处在于 ①它揭示了方程这一数学思想方法的目标:为了求未知数 ②陈述了“己知数”的存在,解方程需要充分利用己知数和未知数之间的关系: ③方程的本质是“关系”,而且是一个等式关系。 在高等数学中方程的定义:形如fx,2,.,x)=g化,x2,.,x)的等式叫做方程,其中 fx,x2,xgk,x2,.,x)是在它们定义域的交集内研究的两个解析式,且至少有一个不是 常函数。 (口方程的分类 指数方程 超越方程 对数方程 三角方程 反三角方程 方程 一次方程 整式方程二次方程 有理方程 代数方程 高次方程 分式方程 无理方程 三、一元方程的同解性 定义1如果方程()(x)=g(x)的任何一个解都是方程(2)f5(x)=g2(x)的解,并且方程2)的任 何一个解也都是方程1)的解,那么方程()和(2称为同解方程。 两个无解方程认为是同解方程。 定理1如果函数A(x)对于方程f(x)=g(x)的定义域M中的数都有意义,那么方程) 第2页共14页
初等代数研究 第2页 共14页 与方程,二阶矩阵与二元一次方程组、一阶线性差分方程、参数方程等等。 ㈢方程的科学价值 自学教材《中学代数研究》P62~63。 二、方程的定义 ㈠方程的几种定义 目前中学数学教科书中通用的方程定义是:含有未知数的等式。但是,形如 sin cos 1,( 1) 2 1 2 2 2 2 x + x = x + = x + x + 之类的等式难以界定。 给出一个可以取代的定义:方程是为了求未知数,在未知数和已知数之间建立的一种等式关系。 好处在于 ①它揭示了方程这一数学思想方法的目标:为了求未知数; ②陈述了“已知数”的存在,解方程需要充分利用已知数和未知数之间的关系; ③方程的本质是“关系”,而且是一个等式关系。 在高等数学中方程的定义:形如 ( ) ( ) n n f x , x , , x g x , x , , x 1 2 = 1 2 的等式叫做方程,其中 ( ) ( ) n n f x , x , , x , g x , x , , x 1 2 1 2 是在它们定义域的交集内研究的两个解析式,且至少有一个不是 常函数。 ㈡方程的分类 无理方程 分式方程 高次方程 二次方程 一次方程 整式方程 有理方程 代数方程 反三角方程 三角方程 对数方程 指数方程 超越方程 方程 三、一元方程的同解性 定义 1 如果方程⑴ f (x) g (x) 1 = 1 的任何一个解都是方程⑵ f (x) g (x) 2 = 2 的解,并且方程⑵的任 何一个解也都是方程⑴的解,那么方程⑴和⑵称为同解方程。 两个无解方程认为是同解方程。 定理 1 如果函数 A(x) 对于方程 f (x) = g(x) 的定义域 M 中的数都有意义,那么方程⑴

初等代数研究 f(x)=g(x)与方程2)f(x)+A(x)=g(x)+Ax)同解。 设x,∈M,且有fx)=g(x),从而有fx)+4(x)=g(x)+A(x),即方程f(x)=g(x) 的每一个解都是方程f(x)+A(x)=g(x)+A(x)的解。 如果fx)+A(x)=g(x)+Ax),由fx)+Ax)-A(x)=g(x)+4(x)-4A(x) 可得fx)=g(x),即方程fx)+A(x)=g(x)+4(x)的每一个解也都是方程f(x)=g(x)的解 这两个方程是同解方程。 定理2如果函数A(x)对于方程f(x)=g(x)的定义域M中的数都有意义,并且不等于零,那么 方程(fx)=g(x)与方程(2)A(x)fx)=A(x)g(x)同解。 定理3如果F(x)=f(x)∫(x).f(x),那么方程Fx)=0的解集等于下列各个方程: f(x)=0,f5(x)=0,.,f(x)=0 的解集的并集,其中每一个解都属于这k个方程的定义域的交集。 定理4如果fx)=f(x),8(x)=82(x),方程)f(x)=81(x)与方程(2f(x)=g(x)的定 义域都是数集M,那么方程)与方程(2)同解。 四、几种常见方程的变形 在解方程时,除了利用同解变形外,有时还要作以下几种变形: 1,方程∫(x)=g”(x)是方程f(x)=g(x)的结果:正整数n是对函数f(x,g(x)施行乘方运 算的指数。可能产生增根,如2x-1=3x+5 2.方程f(x)=g(x)是方程Vf(x)=yg(x)的结果,不小于2的整数n是对函数f(x),g(x) 施行开方运算的根指数(n为偶数时,f(x)≥0,g(x)≥0) 3如果。g,)不等于0,那么方程牌=是方程0=的结果。 81(x)82(x) 4如果对于定义域中的数(x)≠g(x,且(x)≠8(x),那么方程 )+8田-国+8因是方程四=的结果。 f(x)-g(x)∫5(x)-g2(x) g(x)g2(x) 第3页共14页
初等代数研究 第3页 共14页 f (x) = g(x) 与方程⑵ f (x) + A(x) = g(x) + A(x) 同解。 证 设 x1 M ,且有 ( ) ( ) 1 1 f x = g x ,从而有 ( ) ( ) ( ) ( ) 1 1 1 1 f x + A x = g x + A x ,即方程 f (x) = g(x) 的每一个解都是方程 f (x) + A(x) = g(x) + A(x) 的解。 如果 ( ) ( ) ( ) ( ) 1 1 1 1 f x + A x = g x + A x ,由 ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 1 1 f x + A x − A x = g x + A x − A x , 可得 ( ) ( ) 1 1 f x = g x ,即方程 f (x) + A(x) = g(x) + A(x) 的每一个解也都是方程 f (x) = g(x) 的解 这两个方程是同解方程。 定理 2 如果函数 A(x) 对于方程 f (x) = g(x) 的定义域 M 中的数都有意义,并且不等于零,那么 方程⑴ f (x) = g(x) 与方程⑵ A(x) f (x) = A(x)g(x) 同解。 定理 3 如果 ( ) ( ) ( ) ( ) 1 2 F x f x f x f x = k ,那么方程 F(x) = 0 的解集等于下列各个方程: f 1 (x) = 0, f 2 (x) = 0, , f k (x) = 0 的解集的并集,其中每一个解都属于这 k 个方程的定义域的交集。 定理 4 如果 ( ) ( ), ( ) ( ) 1 2 1 2 f x f x g x g x ,方程⑴ ( ) ( ) 1 1 f x = g x 与方程⑵ ( ) ( ) 2 2 f x = g x 的定 义域都是数集 M ,那么方程⑴与方程⑵同解。 四、几种常见方程的变形 在解方程时,除了利用同解变形外,有时还要作以下几种变形: ⒈方程 f (x) g (x) n n = 是方程 f (x) = g(x) 的结果;正整数 n 是对函数 f (x), g(x) 施行乘方运 算的指数。可能产生增根,如 4 4 2x −1 = 3x + 5 ⒉方程 f (x) = g(x) 是方程 n n f (x) = g(x) 的结果,不小于 2 的整数 n 是对函数 f (x), g(x) 施行开方运算的根指数( n 为偶数时, f (x) 0, g(x) 0 ) ⒊如果 ( ), ( ) 1 2 g x g x 不等于 0,那么方程 ( ) ( ) ( ) ( ) 2 2 1 1 g x f x g x f x = 是方程 ( ) ( ) ( ) ( ) 2 2 1 1 f x g x f x g x = 的结果。 ⒋如果对于定义域中的数 ( ) ( ) 1 1 f x g x ,且 ( ) ( ) 2 2 f x g x ,那么方程 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 1 1 1 1 f x g x f x g x f x g x f x g x − + = − + 是方程 ( ) ( ) ( ) ( ) 2 2 1 1 g x f x g x f x = 的结果

初等代数研究 5.方程fx)=g()是方程gfx)=ggx)的结果。 6.方程fx)=gx)是方程snfx)=sng(x)的结果 第4项共14页
初等代数研究 第4页 共14页 ⒌方程 f (x) = g(x) 是方程 lg f (x) = lg g(x) 的结果。 ⒍方程 f (x) = g(x) 是方程 sin f (x) = sin g(x) 的结果

初等代数研究 五、解方程的常用方法 (换元法 例1解方程(6x+7}(3x+4)(x+1)=6 解 令3x+号-y,则6+7=23x+4=)+宁x41-0-片原方程支形为 2°0+20-2-18 即 4y-y2-18=0 解之得y2=9,2三一之所以得到如下四个解 h=为=-y=5,y=-2 换回原来变量得到原方程的解 7.5 对于形如fk,Va2-x2)=0或f,Vx2-a2=0或fx,Vx2+a2)=0的方程,可以引入 三角代换使方程化为较简单的三角方程来求解。关键是使根号内的部分可以成为完全平方式,以便 去掉根号。 形如f(x)+b州fx)+c=0的方程,可令y=fx),将方程化为关于y的整式方程。 +b ]+c=0或df]+g] )] +b=0的分式方程,可令 Lg() f(x) =f因,化为一个整式方程am2+b加+c=0. g(x) 课堂练习1解方程12x4-56x3+89x2-56x+12=0 将方程表示为12(x+)-563+x)+89x2=0 因为x生0,格方程青瑞案以宁,得 x+,则+少-2,从有 12(y2-2)-56y+89=0 第5页共14项
初等代数研究 第5页 共14页 五、解方程的常用方法 ㈠换元法 例 1 解方程 (6 7) (3 4)( 1) 6 2 x + x + x + = 解 令 x + = y 2 7 3 ,则 ) 2 1 ( 3 1 , 1 2 1 6x + 7 = 2y,3x + 4 = y + x + = y − 。原方程变形为 ( ) ) 18 2 1 )( 2 1 2 ( 2 y y + y − = 即 4 18 0 4 2 y − y − = 解之得 2 1 , 4 2 9 2 y = y = − 。所以得到如下四个解 y y , y 2i, y 2i 2 3 , 2 3 1 = 2 = − 3 = 4 = − 换回原来变量得到原方程的解 x x x i x i 3 2 6 7 , 3 2 6 7 , 3 5 , 3 2 1 = − 2 = − 3 = − + 4 = − − 对于形如 ( , ) 0 2 2 f x a − x = 或 ( , ) 0 2 2 f x x − a = 或 ( , ) 0 2 2 f x x + a = 的方程,可以引入 三角代换使方程化为较简单的三角方程来求解。关键是使根号内的部分可以成为完全平方式,以便 去掉根号。 形如 a( f (x)) + b f (x) + c = 0 m n m 的方程,可令 m y = f (x) ,将方程化为关于 y 的整式方程。 形如 0 ( ) ( ) ( ) ( ) 2 + = + c g x f x b g x f x a 或 0 ( ) ( ) ( ) ( ) + = + b f x g x c g x f x a 的分式方程,可令 ( ) ( ) g x f x u = ,化为一个整式方程 0 2 au + bu + c = 。 课堂练习 1 解方程 12 56 89 56 12 0 4 3 2 x − x + x − x + = 解 将方程表示为 12( 1) 56( ) 89 0 4 3 2 x + − x + x + x = 因为 x 0 ,将方程两端乘以 2 1 x ,得 ) 89 0 1 ) 56( 1 12( 2 2 + − + + = x x x x 设 y x x + = 1 ,则 2 1 2 2 2 + = y − x x ,从而有 12( 2) 56 89 0 2 y − − y + =

初等代数研究 由此得y=多或y= 13 x 6 -2对捐 口引入参数法 例2已如实数x山病足子-后-兰求华本的。 y u x' 解法一 令=上=三-”=,则x=y==ku=所以 y Z u x x+y+2+M=k(x+y++) 故 (x+y++k-I)=0 于是x+y+z+u=0或k=1 若x+y+:+W=0,则+y+:+ =0 x+y+:-u 若k=1,则x=y=:=,所以+y++”=2 x+y+z-u 解法二 令==三=“=k,则x=y=k2:=k3=kx,所以k=1,k= y z u x 若k=1,则+y+:+”==2 x+y+:-u2x 小-00 白二项方程和三项方程的解法 形如x”一A=0的方程叫做二项方程,解此方程就是求A的n次方根。 定理如果c=r(cos0+ism),那么二项方程x”-c=0的根是 第6项共14项
初等代数研究 第6页 共14页 由此得 2 5 y = 或 6 13 y = 。 由 2 1 5 + = x x 或 6 1 13 + = x x 解得 3 2 , 2 3 , 2 1 x = 2, ㈡引入参数法 例 2 已知实数 x, y,z,u 满足 x u u z z y y x = = = ,求 x y z u x y z u + + − + + + 的值。 解法一 令 k x u u z z y y x = = = = ,则 x = ky, y = kz,z = ku,u = kx. 所以 x + y + z + u = k(x + y + z + u) 故 (x + y + z + u)(k −1) = 0 于是 x + y + z + u = 0 或 k =1 若 x + y + z + u = 0 ,则 = 0 + + − + + + x y z u x y z u 若 k =1 ,则 x = y = z = u ,所以 = 2 + + − + + + x y z u x y z u 解法二 令 k x u u z z y y x = = = = ,则 x ky k z k u k x 2 3 4 = = = = ,所以 1 4 k = ,k = 1 若 k =1 ,则 2 2 4 = = + + − + + + x x x y z u x y z u 若 k = −1 ,则 0 2 0 = = + + − + + + x y z u k x y z u ㈢二项方程和三项方程的解法 形如 x − A = 0 n 的方程叫做二项方程,解此方程就是求 A 的 n 次方根。 定理 如果 c = r(cos + isin ) ,那么二项方程 x − c = 0 n 的根是

初等代数研究 Fcos0+2kr+1sn0+2k.k=012,n-1. 例3解方程x-32=0 解 x5=32(cosπ+isnπ) 所以x=20os+2红+1sm+2“Xk=0L23,4) 5 形如x2+m”+q=0的方程叫做三项方程,特别当n=2时,得方程x+x2+q=0,称 为双二次方程。 例4解方程x6-4x3+3=0 解 设x3=y,有 y2-4y+3=0 解得乃=1,乃2=3,再分别解方程x=1和x2=3,可得原方程的解为 名=儿=+ 2 =片=5=5=生x=片 2 2 四因式分解法 例5解方程x-12x+323=0 解 x4-12x+323=(x4+36x2+324)-(36x2+12r+1) =(x2+18)2-(6x+1)2 =(x2+6x+19(x2-6x+17) 所以原方程同解与方程(x2+6x+19(x2-6x+17)=0 故方程的解为 x=-3+V10i,x=-3-V10i,x3=3+2W2i,x4=3-2√2i (田图像法 例6确定方程2+x2=V2的实数解的个数。 解 第7页共14页
初等代数研究 第7页 共14页 ), 0,1,2, , 1 2 sin 2 (cos = − + + + k n n k i n k r n 。 例 3 解方程 32 0 5 x − = 解 32(cos sin ) 5 x = + i 所以 )( 0,1,2,3,4) 5 2 sin 5 2 2(cos = + + + = k k i k x 形如 0 2 x + px + q = n n 的方程叫做三项方程,特别当 n = 2 时,得方程 0 4 2 x + px + q = ,称 为双二次方程。 例 4 解方程 4 3 0 6 3 x − x + = 解 设 x = y 3 ,有 4 3 0 2 y − y + = 解得 y1 =1, y2 = 3 ,再分别解方程 1 3 x = 和 3 3 x = ,可得原方程的解为 3 2 6 3 5 3 4 2 1 2 3 ) 2 1 3 , 3( 2 1 3 ) , 3, 3 2 1 3 , ( 2 1 3 1, i x i x x i x i x x − + = − + = = − + = − + = = ㈣因式分解法 例 5 解方程 12 323 0 4 x − x + = 解 ( 6 19)( 6 17) ( 18) (6 1) 12 323 ( 36 324) (36 12 1) 2 2 2 2 2 4 4 2 2 = + + − + = + − + − + = + + − + + x x x x x x x x x x x x 所以原方程同解与方程 ( 6 19)( 6 17) 0 2 2 x + x + x − x + = 故方程的解为 x 3 10i, x 3 10i, x 3 2 2i, x 3 2 2i 1 = − + 2 = − − 3 = + 4 = − ㈤图像法 例 6 确定方程 2 2 2 + = − x x 的实数解的个数。 解
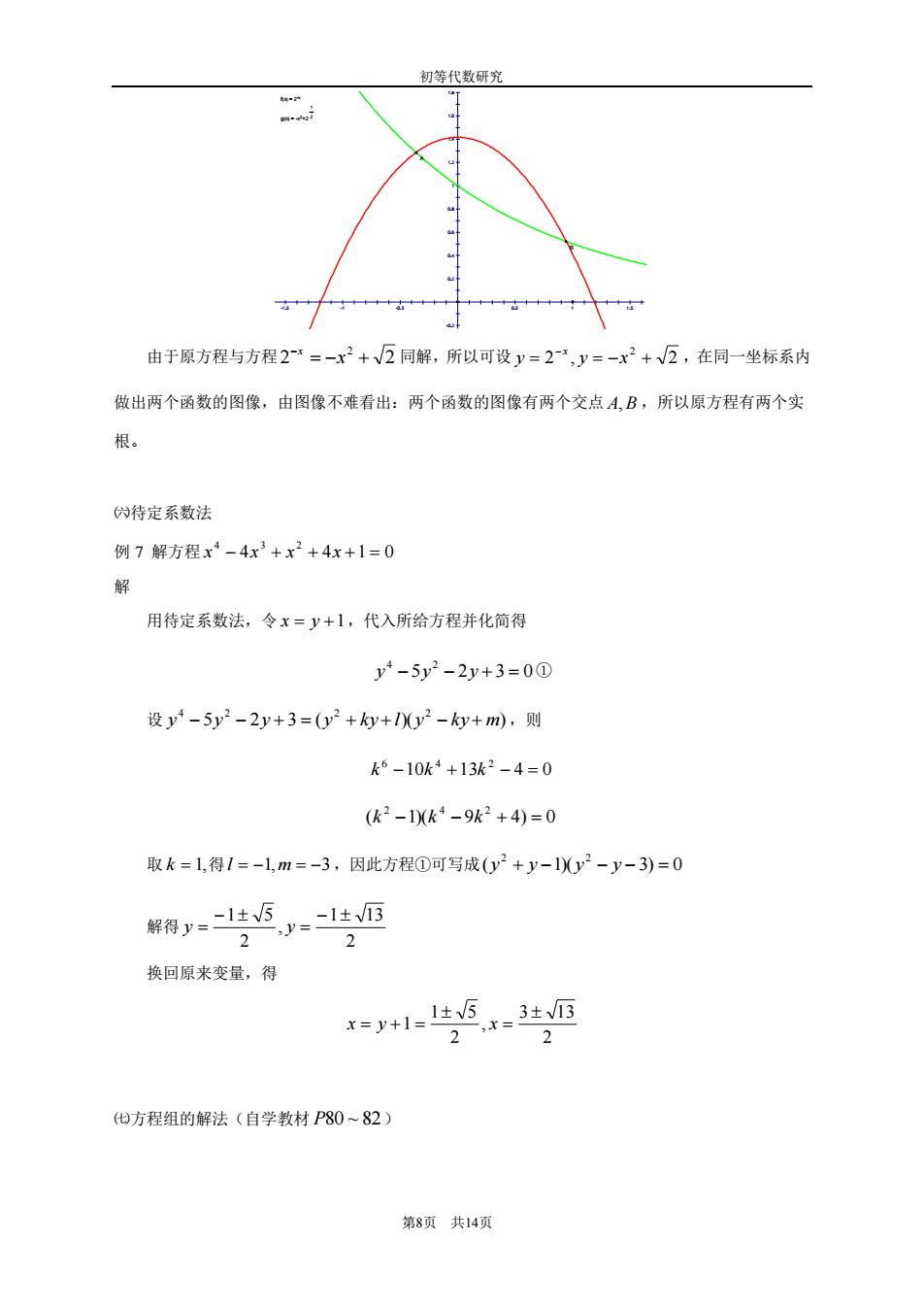
初等代数研究 由于原方程与方程2=-x2+√互同解,所以可设y=2,y=-x2+√2,在同一坐标系内 做出两个函数的图像,由图像不难看出:两个函数的图像有两个交点A,B,所以原方程有两个实 根。 伪待定系数法 例7解方程x-4x3+x2+4x+1=0 解 用待定系数法,令x=y+1,代入所给方程并化简得 y-5y2-2y+3=0@ 设y-5y2-2y+3=0y2++10y2-y+m),则 k6-10k4+132-4=0 (k2-10k-9k2+4)=0 取k=1,得1=-1,m=-3,因此方程①可写成0y2+y-1y2-y-3)=0 2 2 换回原来变量,得 =+1=±5 (他方程组的解法(自学教材P80~82) 第8项共14项
初等代数研究 第8页 共14页 1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 -0.2 -1.5 -1 -0.5 0.5 1 1.5 g(x) = -x 2+2 1 2 f(x) = 2 -x A B 由于原方程与方程 2 2 2 = − + − x x 同解,所以可设 2 , 2 2 = = − + − y y x x ,在同一坐标系内 做出两个函数的图像,由图像不难看出:两个函数的图像有两个交点 A, B ,所以原方程有两个实 根。 ㈥待定系数法 例 7 解方程 4 4 1 0 4 3 2 x − x + x + x + = 解 用待定系数法,令 x = y +1 ,代入所给方程并化简得 5 2 3 0 4 2 y − y − y + = ① 设 5 2 3 ( )( ) 4 2 2 2 y − y − y + = y + k y + l y − k y + m ,则 10 13 4 0 6 4 2 k − k + k − = ( 1)( 9 4) 0 2 4 2 k − k − k + = 取 k = 1, 得 l = −1,m = −3 ,因此方程①可写成 ( 1)( 3) 0 2 2 y + y − y − y − = 解得 2 1 13 , 2 1 5 − = − y = y 换回原来变量,得 2 3 13 , 2 1 5 1 = x = y + = x ㈦方程组的解法(自学教材 P80 ~ 82 )

初等代数研究 作业一 1防32 9 2.解方程√2x-6+√x+4=5 3.解方程1og2(x+2)+l0g2(3x-4)=4 4解方程x62云=4 5.解方程g1+x+3g1-x=g1-x2+2 6.解方程sinx-2cosx=2 摘自《初等代数研究》(下册)P330~331 7.解方程6x4-25x3+12x2+25x+6=0 摘自《初等代数研究》(下册)P342~343 8解方程x3=8 9.解方程组 「x+y+z=0 x2+y2-2=20 x+y4-=4=560 摘自《初等代数研究》(下册)P371~372 第9页共14页
初等代数研究 第9页 共14页 作业一 ⒈解方程 1 1 2( 4) 9 2( 1) 1 − + + = − + x x x x ⒉解方程 2x − 6 + x + 4 = 5 ⒊解方程 log 2 (x + 2) + log 2 (3x − 4) = 4 ⒋解方程 4 log 2 = x x x ⒌解方程 lg 1 3lg 1 lg 1 2 2 + x + − x = − x + ⒍解方程 sin x − 2cos x = 2 摘自《初等代数研究》(下册) P330 ~ 331 ⒎解方程 6 25 12 25 6 0 4 3 2 x − x + x + x + = 摘自《初等代数研究》(下册) P342 ~ 343 ⒏解方程 8 3 x = ⒐解方程组 + − = + − = + + = 560 20 0 4 4 4 2 2 2 x y z x y z x y z 摘自《初等代数研究》(下册) P371~ 372

初等代数研究 六、一元三次、四次以及高次方程 (一元三次方程的解法 设有一般三次方程x+bx2+x+d=0a≠0),取x=y-名,整理得到 +++(器先+=-00 两端除以a得到 y+py+q=0② a 27a 3a 作变换y=u+v,代入方程②,整理得到 3+v3+q+(3m+pu+)=0 要求3n+p=0,则变为+t+9=0 3w+D=0 从而 其中0=1+5o.1- 2 -}-图+号=m= 8浓程+++名=0 解 b 2 作支换=少名y装=少-号代入方程,整理得到)广+四+q=0,其中 223x23 X- 27297 27-+贸 再做变换y-}:,并整理得到:2-15:+22=0 利用求根公式可以得到 第10页共14页
初等代数研究 第10页 共14页 六、一元三次、四次以及高次方程 ㈠一元三次方程的解法 设有一般三次方程 0( 0) 3 2 ax + bx + cx + d = a ,取 a b x y 3 = − ,整理得到 ) 0 27 3 2 ) ( 3 ( 2 2 3 3 + − + + − + d = a bc a b c y a b ay ① 两端除以 a 得到 0 3 y + py + q = ② 其中 ) 27 3 2 ( 1 ), 3 ( 1 2 2 3 d a bc a b a c q a b a p = − + = − + 。 作变换 y = u + v ,代入方程②,整理得到 (3 )( ) 0 3 3 u + v + q + uv + p u + v = 要求 3uv + p = 0 ,则变为 + + = + = 0 3 0 3 3 u v q uv p 解得, 2 4 27 , 2 4 27 2 3 3 2 3 3 q q p v q q p u = − + + = − − + 从而 1 2 2 1 3 3 2 3 1 1 2 2 1 3 3 2 3 1 , , 2 4 27 , , 2 4 27 v v v v q q p v u u u u q q p u = − − + = = = − + + = = 其中 2 1 3 , 2 1 3 2 i − − i = − + = 例 8 解三次方程 0 16 27 4 27 4 3 27 2 x + x + x + = 解 作变换 4 9 3 1 4 27 3 = − = − = y − y a b x y ,代入方程,整理得到 0 3 y + py + q = ,其中 ( ) ( ) 32 297 16 27 3 1 4 27 4 27 27 1 4 27 2 ) 27 3 2 ( 1 , 16 135 4 27 3 1 4 27 ) 3 ( 1 3 2 3 2 2 + = − = + = − = − + = − + = − d a bc a b a c q a b a p 再做变换 y z 4 3 = ,并整理得到 15 22 0 3 z − z + = 利用求根公式可以得到