
第十七讲 1体积的概念 (1)两个合同的多面体有相同的体积 ■(2)两多面体V,V的和V的体积等于V,V体积之和。假设这样的对应存在, 即多面体的体积存在。 2求立体体积的基础 ■定理1:长方体的体积等于长宽高三维的乘积 ■系:立方体的体积等于一棱的立方 4.11.1 ·祖氏原理:设两立体夹在两平行平面a,B之间,若以介于a,B间的任一平行面 Y截之,所得截面积恒相等,则两立体等积. Y 图4.633 ■定理2:平行六面体的体积等于底面积乘以高。将平行六面体进行分割,得到 ■定理3】 三棱柱体积等于底面积乘以高。任意棱柱可以分割为三棱柱,得到 。定理4:棱柱体积等于底面积乘以高。 概念 ■斜棱柱,直棱柱,正棱柱,直截面, ■枝柱侧面积: ■定理5:棱柱的侧面积等于直截面周长跟侧棱的积
第十七讲 1 体积的概念 ◼ (1)两个合同的多面体有相同的体积 ◼ (2)两多面体V,V‘的和V’‘的体积等于V,V’体积之和.假设这样的对应存在, 即多面体的体积存在. 2求立体体积的基础 ◼ 定理1:长方体的体积等于长宽高三维的乘积. ◼ 系:立方体的体积等于一棱的立方. §4.11.1 ◼ 祖氏原理:设两立体夹在两平行平面α,β之间,若以介于α,β间的任一平行面 γ截之,所得截面积恒相等,则两立体等积. ◼ 定理2:平行六面体的体积等于底面积乘以高.将平行六面体进行分割,得到 ◼ 定理3:三棱柱体积等于底面积乘以高.任意棱柱可以分割为三棱柱,得到 ◼ 定理4:棱柱体积等于底面积乘以高. 概念 ◼ 斜棱柱,直棱柱,正棱柱,直截面, ◼ 棱柱侧面积: ◼ 定理5:棱柱的侧面积等于直截面周长跟侧棱的积.
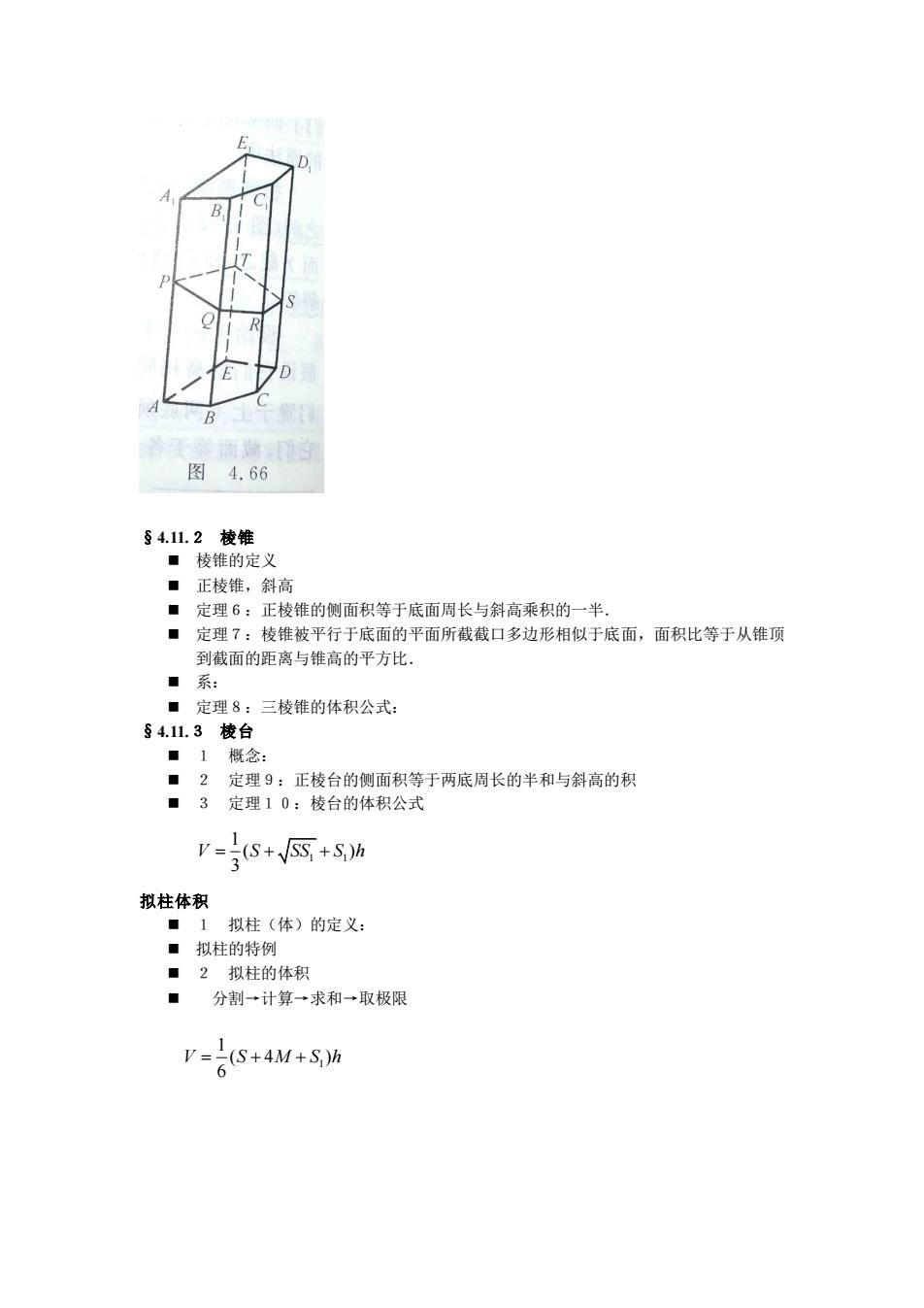
图4.66 8411.2棱锥 ■棱锥的定义 ■正棱锥,斜高 ·定理6:正棱锥的侧面积等于底面周长与斜高乘积的一半. ■定理7:棱锥被平行于底面的平面所截截口多边形相似于底面,面积比等于从锥顶 到截面的距离与锥高的平方比. ■系: ■定理8: 三棱锥的体积公式: §4.1山.3棱台 ■1概念: ■2定理9:正棱台的侧面积等于两底周长的半和与斜高的积 ■3定理10:棱台的体积公式 V=(S++)h 拟柱体积 ■1拟柱(体)的定义: ·拟柱的特例 2拟柱的体积 ·分割一计算一求和一取极限 -(5
§4.11.2 棱锥 ◼ 棱锥的定义 ◼ 正棱锥,斜高 ◼ 定理6:正棱锥的侧面积等于底面周长与斜高乘积的一半. ◼ 定理7:棱锥被平行于底面的平面所截截口多边形相似于底面,面积比等于从锥顶 到截面的距离与锥高的平方比. ◼ 系: ◼ 定理8:三棱锥的体积公式: §4.11.3 棱台 ◼ 1 概念: ◼ 2 定理9:正棱台的侧面积等于两底周长的半和与斜高的积 ◼ 3 定理10:棱台的体积公式 拟柱体积 ◼ 1 拟柱(体)的定义: ◼ 拟柱的特例 ◼ 2 拟柱的体积 ◼ 分割→计算→求和→取极限 1 1 1 ( ) 3 V S SS S h = + +1 1 ( 4 ) 6 V S M S h = + +
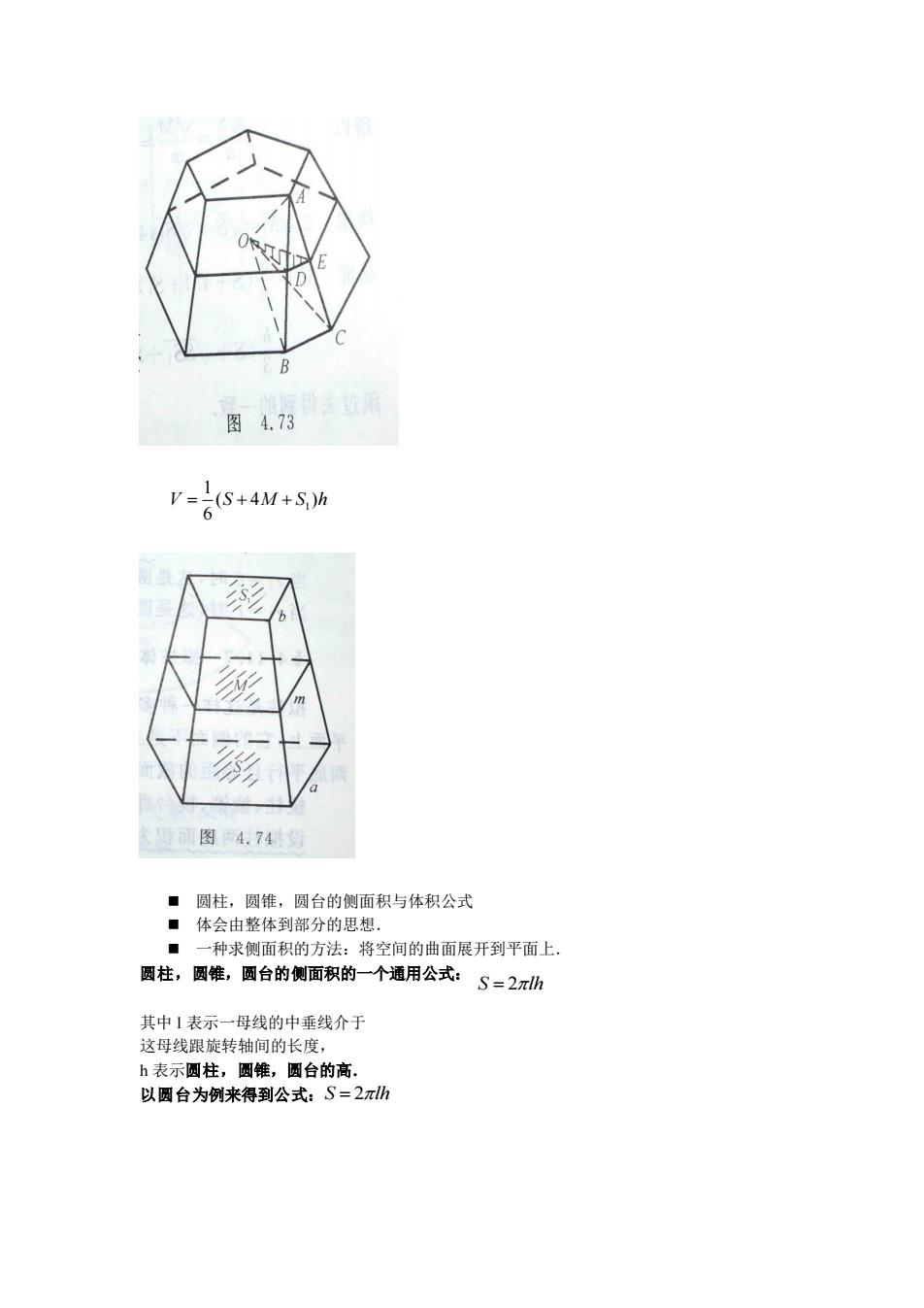
图4.73 V-1(S+4M+S)h 图4.74 ■圆柱,圆锥,圆台的侧面积与体积公式 ■体会由整体到部分的思想 一种求侧面积的方法:将空间的曲面展开到平面上 圆柱,圆锥,圆台的侧面积的一个通用公式:S=2xh 其中1表示一母线的中垂线介于 这母线跟旋转轴间的长度, h表示圆柱,圆锥,台的高 以圆台为例来得到公式:S=2πW
◼ 圆柱,圆锥,圆台的侧面积与体积公式 ◼ 体会由整体到部分的思想. ◼ 一种求侧面积的方法:将空间的曲面展开到平面上. 圆柱,圆锥,圆台的侧面积的一个通用公式: 其中 l 表示一母线的中垂线介于 这母线跟旋转轴间的长度, h 表示圆柱,圆锥,圆台的高. 以圆台为例来得到公式: 1 1 ( 4 ) 6 V S M S h = + + S lh = 2 S lh = 2

班承 图475 球→球带,球冠,球缺,球扇形 ·1球带的概念 ■2球带面积的计算(分割一计算一求和一取极限) ■定理11:球带的面积公式 S球带=2πh 图4.76 ■系:同球的两个球带面积之比等于他们的高之比 ■定理12:球的表面积等于大圆面积的4倍 球扇形,球,球缺的体积 (部分→整体→部分) a 4.77
球→球带,球冠,球缺,球扇形 ◼ 1 球带的概念 ◼ 2 球带面积的计算(分割→计算→求和→取极限) ◼ 定理11:球带的面积公式 ◼ 系:同球的两个球带面积之比等于他们的高之比. ◼ 定理12:球的表面积等于大圆面积的4倍 球扇形,球,球缺的体积 (部分→整体→部分) S rh 球带 = 2 2 1 3 2 3 V S r r h = = 球扇 球带

球缺的体积 ■球缺的概念 ■球缺的体积公式 ■定理15:设球半径为r,球缺的高为h则球缺的体积为: 装=h(-名
球缺的体积 ◼ 球缺的概念 ◼ 球缺的体积公式 ◼ 定理15:设球半径为 r,球缺的高为 h,则球缺的体积为: 2 ( ) 3 h V h r 球缺 = −