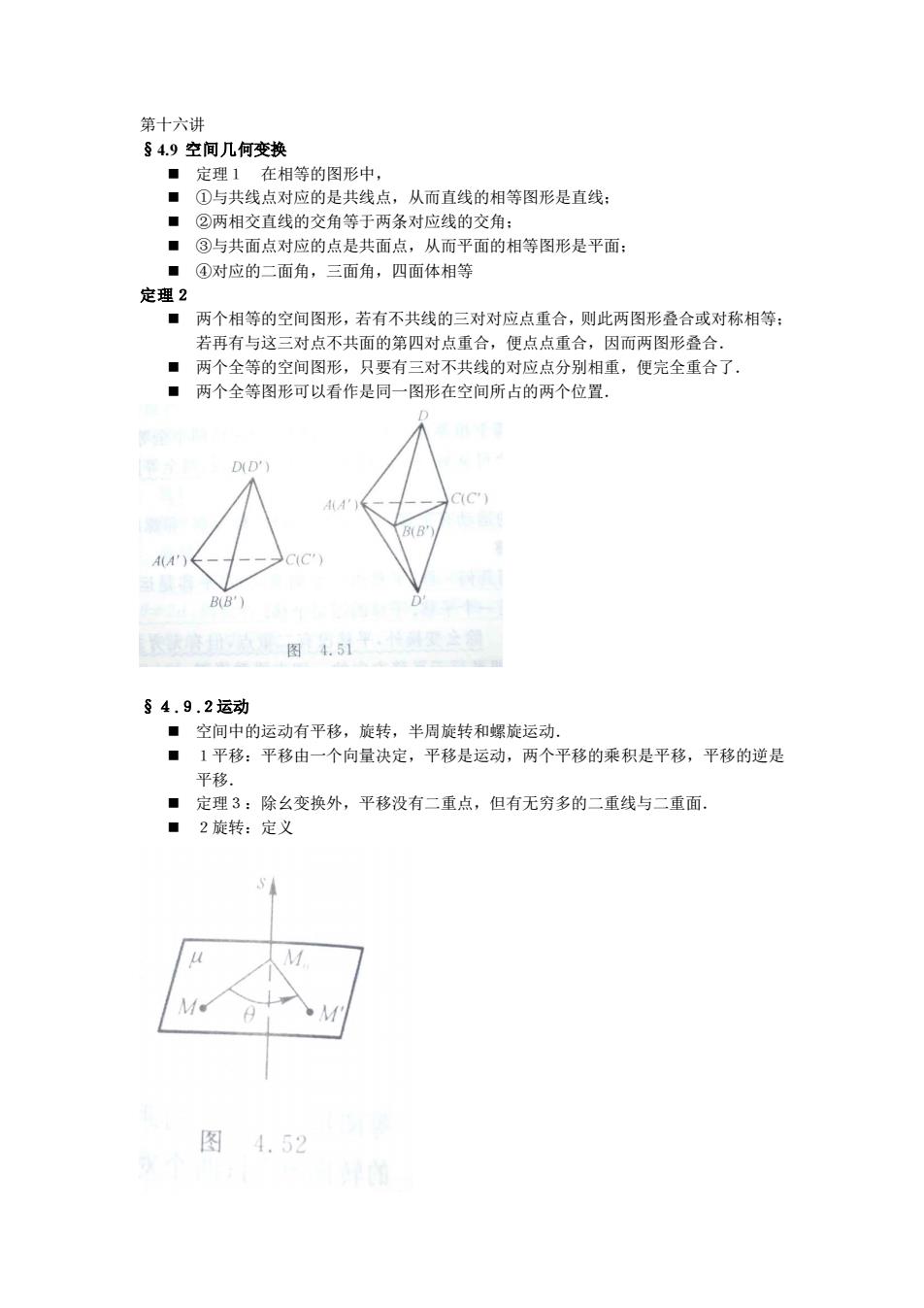
第十六讲 §4.9空间几何变 ·定理1 在相等的图形中 ·①与共线点对应的是共线点,从而直线的相等图形是直线: ■②两相交直线的交角等于两条对应线的交角: ■③与共面点对应的点是共面点,从而平面的相等图形是平面: ■④对应的二面角,三面角,四面体相等 定理2 两个相等的空间图形,若有不共线的三对对应点重合,则此两图形叠合或对称相等: 若再有与这三对点不共面的第四对点重合,便点点重合,因而两图形叠合. ■两个全等的空间图形,只要有三对不共线的对应点分别相重,便完全重合了. ■两个全等图形可以看作是同一图形在空间所占的两个位置. 图4.51 §4.9.2运动 ■空间中的运动有平移,旋转,半周旋转和螺旋运动. ■1平移:平移由一个向量决定,平移是运动,两个平移的乘积是平移,平移的逆是 平移. ■定理3:除么变换外,平移没有二重点,但有无穷多的二重线与二重面。 ■2旋转:定义 图4.52
第十六讲 §4.9 空间几何变换 ◼ 定理1 在相等的图形中, ◼ ①与共线点对应的是共线点,从而直线的相等图形是直线; ◼ ②两相交直线的交角等于两条对应线的交角; ◼ ③与共面点对应的点是共面点,从而平面的相等图形是平面; ◼ ④对应的二面角,三面角,四面体相等 定理2 ◼ 两个相等的空间图形,若有不共线的三对对应点重合,则此两图形叠合或对称相等; 若再有与这三对点不共面的第四对点重合,便点点重合,因而两图形叠合. ◼ 两个全等的空间图形,只要有三对不共线的对应点分别相重,便完全重合了. ◼ 两个全等图形可以看作是同一图形在空间所占的两个位置. §4.9.2运动 ◼ 空间中的运动有平移,旋转,半周旋转和螺旋运动. ◼ 1平移:平移由一个向量决定,平移是运动,两个平移的乘积是平移,平移的逆是 平移. ◼ 定理3:除幺变换外,平移没有二重点,但有无穷多的二重线与二重面. ◼ 2旋转:定义

■定理4:旋转是运动 定理5:旋转(0)和(0)的积是一个旋转(0十0”) ◆ 定理6:旋转(s0)的逆是旋转 (s-0). 定理7:除么变换外,旋转有无穷多个二重点,若日≠2d,则旋转有一条二重直线 即旋转轴,有无穷多个二重面,即垂直于轴的一切平面。 ■定义:在旋转运动中,若日=2d,则每一点M绕旋转轴转动半圆周,从而M与其 对应点M关于轴S成对称,这样的旋转(s,2d)称为关于S的半周旋转或轴反 M 图4.53 爆旋运动 ■ 一个旋转R跟一个平行于旋转轴的平移T的乘积,称为螺旋运动.两个运动的顺序 不影响结果.即TR=RT ■定理8:螺旋运动是运动. ■定理9:螺旋运动的逆是一个螺旋运动 ■定理10:非单一平移或旋转的螺旋运动没有二重点,但有一条二重线.若旋转角 日≠2d,则螺旋运动没有二重面,但若0=2d则通过轴的平面都是二重面 ■定理11:任意两个全等图形,可以通过一个平移继以两个旋转使相重合,这两旋 转的轴是相交的
◼ 定理4:旋转是运动 ◼ 定理5:旋转(s,θ)和( s,θ’)的积是一个旋转( s, θ+θ’ ) ◼ 定理6:旋转(s,θ)的逆是旋转 (s,-θ). ◼ 定理7:除幺变换外,旋转有无穷多个二重点,若θ≠2d,则旋转有一条二重直线 即旋转轴,有无穷多个二重面,即垂直于轴的一切平面. ◼ 定义:在旋转运动中,若θ= 2d,则每一点M绕旋转轴转动半圆周,从而M与其 对应点M‘关于轴S成对称,这样的旋转(s,2d)称为关于S的半周旋转或轴反射. 螺旋运动 ◼ 一个旋转R跟一个平行于旋转轴的平移T的乘积,称为螺旋运动.两个运动的顺序 不影响结果.即TR=RT. ◼ 定理8:螺旋运动是运动. ◼ 定理9:螺旋运动的逆是一个螺旋运动 ◼ 定理10:非单一平移或旋转的螺旋运动没有二重点,但有一条二重线.若旋转角 θ≠2d,则螺旋运动没有二重面,但若θ=2d 则通过轴的平面都是二重面. ◼ 定理11:任意两个全等图形,可以通过一个平移继以两个旋转使相重合,这两旋 转的轴是相交的.
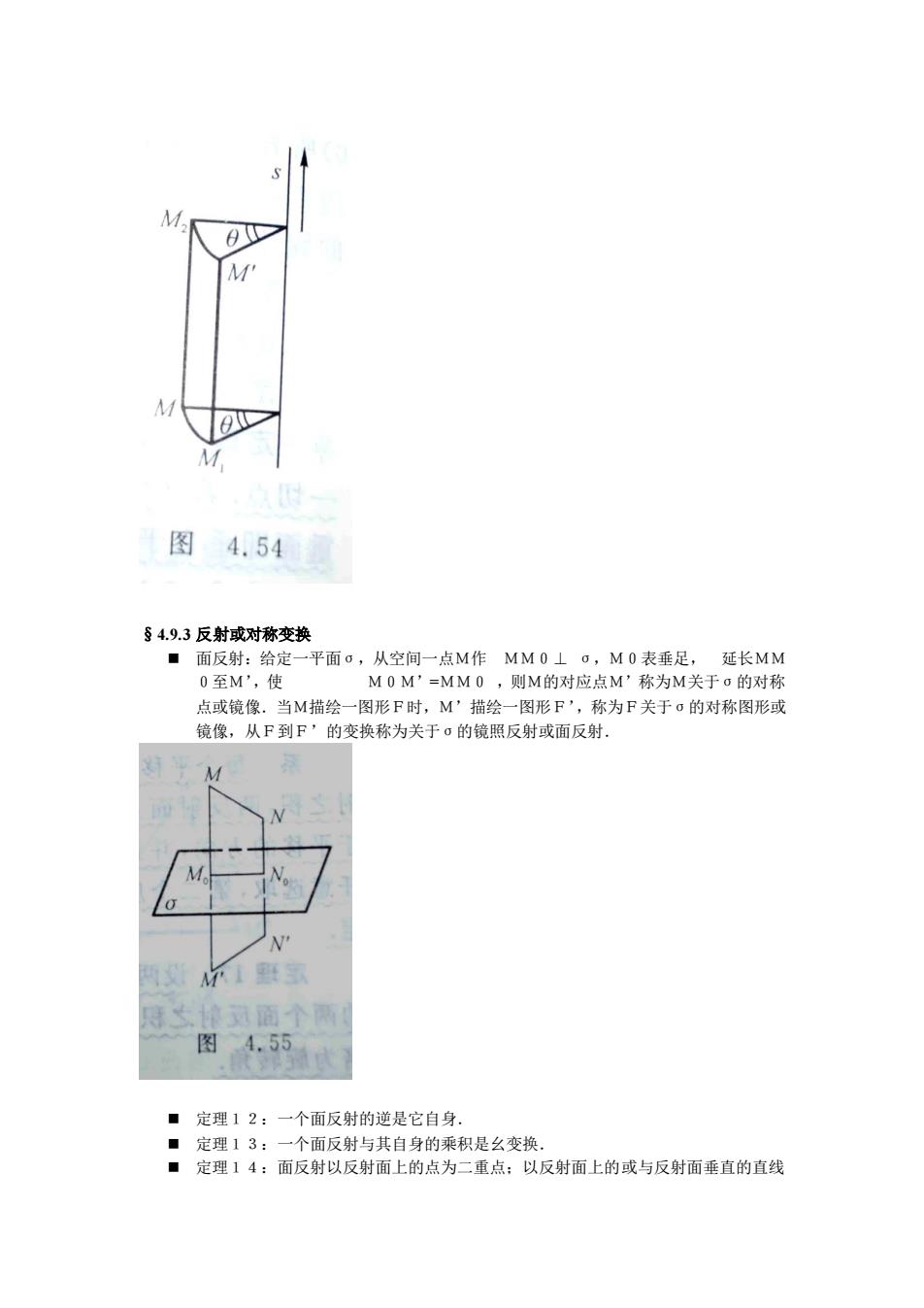
M 图4.54 §4.9.3反射或对称变换 ■面反射:给定,平面,从空间一点M作MM0⊥o,M0表垂足,证长MM 0至M',使 M0M'=MM0,则M的对应点M'称为M关于o的对称 点或镜像。当M描绘一图形F时,M'描绘一图形P',称为F关于。的对称图形 镜像,从F到F’的变换称为关于0的镜照反射或面反射. 面个 图4.55 ■定理12:一个面反射的逆是它自身. ■定理13:一个面反射与其自身的乘积是么变换. ■定理14:面反射以反射面上的点为二重点:以反射面上的或与反射面垂直的直线
§4.9.3 反射或对称变换 ◼ 面反射:给定一平面σ,从空间一点M作 MM0⊥ σ,M0表垂足, 延长MM 0至M’,使 M0M’=MM0 ,则M的对应点M’称为M关于σ的对称 点或镜像.当M描绘一图形F时,M’描绘一图形F’,称为F关于σ的对称图形或 镜像,从F到F’的变换称为关于σ的镜照反射或面反射. ◼ 定理12:一个面反射的逆是它自身. ◼ 定理13:一个面反射与其自身的乘积是幺变换. ◼ 定理14:面反射以反射面上的点为二重点;以反射面上的或与反射面垂直的直线

为二重线:以反射面以及垂直于反射面的平面为二重面】 移. ■系:每个平移可以看作两个面反射之积两反射面互相平行且 垂直于平移方向,其中一个面可任意选取,另一个随之而定. 图4.56 定理17:设两平面。1和。2相交于一直线S,则关于。1和。2的两个反射 面之积是一 个旋转,以S为旋转轴 以。1,02夹角的 倍为旋转角 ■系:每一个旋转可以看作两个面反射之积,两反射面通过旋转轴,其夹角是旋转角 的一半,并且其中一个反射面可以任意选取,另一个便随之而定。 中心反 ■定义:设两占M,M以O为中心,则两点M,M对称于O,O称为对称中心或反 射中心 当O为定点而M在一图形F中变动 ,M的对称点M'所形成的图形F称 为F关于0的对称图形.从F到F·的过程称为中心对称变换或中心反射或点反射 。中心反射保留了图形的距离但改变了转向。所以,心反射和面反射一样,将一图形 F变换为与它相等但全等的图形F', ■定理18:中心反射的逆是它的自身 ■定理19:中心反射与其自身的乘积是么变换 ■定理20:中心反射以反射心为二重点,以通过反射心的直线为二重线:以通过反 射心的平面为二重面. ■定理21:面反射变换中对应的直线或平面相交于反射面上或相平行(重合),中心 反射变换中,对应的直线或平面相平行(或重合). ■定理22:两个心反射之积是一个平移
为二重线;以反射面以及垂直于反射面的平面为二重面. ◼ 定理15:两个面反射的乘积是一个运动. ◼ 定理16:设平面σ1 ∥σ2 ,则关于σ1 和σ2的两个面反射之积等于一个平 移. ◼ 系 : 每 个 平 移 可 以 看 作 两 个 面 反 射 之 积 两 反 射 面 互 相 平行且 垂直于平移方向,其中一个面可任意选取,另一个随之而定. ◼ 定理17:设两平面σ1 和σ2相交于一直线S,则关于σ1 和σ2的两个反射 面之积是一个旋转,以S为旋转轴,以σ1 ,σ2夹角的二倍为旋转角. ◼ 系:每一个旋转可以看作两个面反射之积,两反射面通过旋转轴,其夹角是旋转角 的一半,并且其中一个反射面可以任意选取,另一个便随之而定. 中心反射 ◼ 定义:设两点M,M’以O为中心,则两点M,M’对称于O,O称为对称中心或反 射中心.当O为定点而M在一图形F中变动时,M的对称点M’所形成的图形F’称 为F关于O的对称图形.从F到F’的过程称为中心对称变换或中心反射或点反射. ◼ 中心反射保留了图形的距离但改变了转向.所以,心反射和面反射一样,将一图形 F变换为与它相等但全等的图形F’. ◼ 定理18:中心反射的逆是它的自身. ◼ 定理19:中心反射与其自身的乘积是幺变换. ◼ 定理20:中心反射以反射心为二重点,以通过反射心的直线为二重线;以通过反 射心的平面为二重面. ◼ 定理21:面反射变换中对应的直线或平面相交于反射面上或相平行(重合),中心 反射变换中,对应的直线或平面相平行(或重合). ◼ 定理22:两个心反射之积是一个平移
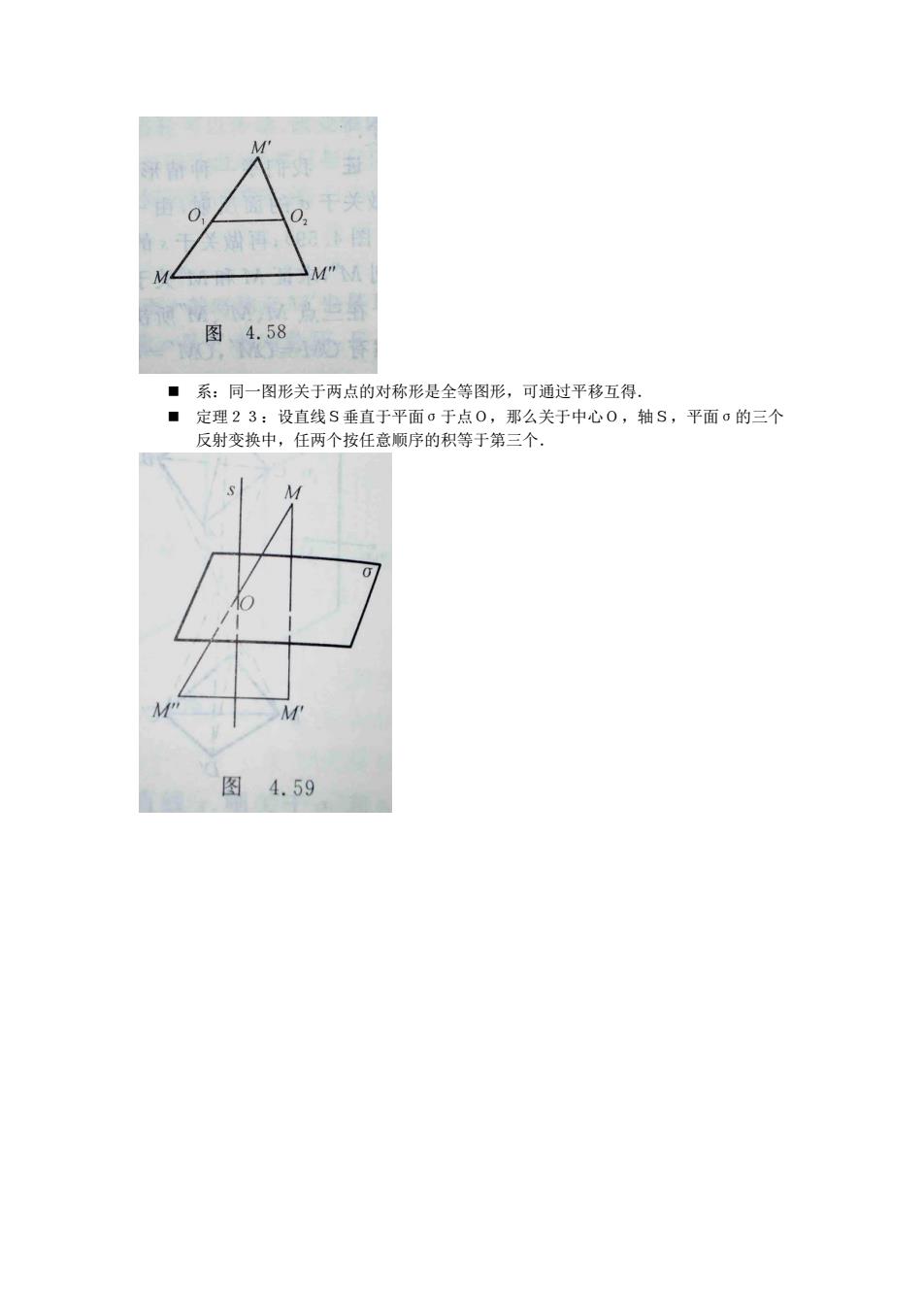
图4.58 ■系:同一图形关于两点的对称形是全等图形,可通过平移互得. ■定理23:设直线S垂直于平面。于点0,那么关于中心0,轴S,平面的三个 反射变换中,任两个按任意顺序的积等于第三个 图4.59
◼ 系:同一图形关于两点的对称形是全等图形,可通过平移互得. ◼ 定理23:设直线S垂直于平面σ于点O,那么关于中心O,轴S,平面σ的三个 反射变换中,任两个按任意顺序的积等于第三个.