
数学能力取决于数学思想方法 一由分析2011年安徽省中考数学试题得到的启示 夏飞(中学特级教师) 应用数学解决问题的能力既是“数学课程标准”中的一 个重要的课程目标,也是考查学生综合素质的一个重要依 据.2011年安徽省中考数学试题就有这样一个特点:不再只 是考查学生积累了多少“双基”,而是考查学生运用“双基” 解决具体问题的办法与能力.重视对逻辑推理能力的考查, 注意适度论证,加强了计算和推理的有机结合,入口容易, 方法多样,不求繁难,也没有出现“偏题”、“怪题”·可 以说,与前两年相比,在保持试题难度框架形式相对稳定不 变的前提下,仍趋向于通过创设新的问题情境,结合实际问 题在运用的过程中考查数学能力,其根本目的是在考查学生 的数学思想方法.不妨在此作些简单分析,与大家共同切磋, 以利教学. 【试题分析】 2011中考数学试题继续延续了2010年的命题思路,注 重基础知识、基本能力和数学思想方法的考查,没有偏题和 怪题,题目难易适中,继续坚持“稳中求变,变中求新”这 一特点 首先,试卷整体布局合理,对知识的考查比较合理、全 面,注重基础知识的考查.整张试卷共23道题.其中选择
数学能力取决于数学思想方法 ──由分析 2011 年安徽省中考数学试题得到的启示 夏 飞(中学特级教师) 应用数学解决问题的能力既是“数学课程标准”中的一 个重要的课程目标,也是考查学生综合素质的一个重要依 据.2011 年安徽省中考数学试题就有这样一个特点:不再只 是考查学生积累了多少“双基”,而是考查学生运用“双基” 解决具体问题的办法与能力.重视对逻辑推理能力的考查, 注意适度论证,加强了计算和推理的有机结合,入口容易, 方法多样,不求繁难,也没有出现“偏题”、“怪题”.可 以说,与前两年相比,在保持试题难度框架形式相对稳定不 变的前提下,仍趋向于通过创设新的问题情境,结合实际问 题在运用的过程中考查数学能力,其根本目的是在考查学生 的数学思想方法.不妨在此作些简单分析,与大家共同切磋, 以利教学. 【试题分析】 2011 中考数学试题继续延续了 2010 年的命题思路,注 重基础知识、基本能力和数学思想方法的考查,没有偏题和 怪题,题目难易适中,继续坚持 “稳中求变,变中求新”这 一特点. 首先,试卷整体布局合理,对知识的考查比较合理、全 面,注重基础知识的考查.整张试卷共 23 道题.其中选择

题共10道题,每题4分;填空题4道题,每题5分;最后 三道题分值分别为12分、12分、14分.代数部分约占48%, 几何部分约占52%.其中代数部分对基础知识和基本能力的 考查,如简单的实数大小比较(第1题)、科学记数法(第 2题)、分式化简(第15题)、一元二次方程的解法(第8 题)、一元一次方程的应用(第16题)、新定义运算(第2、 14题);函数部分考查了一次函数与反比例函数的图像和性 质(第21题)、二次函数的增减性(第23题的3问)及统 计与概率(第5、20题)·几何部分考查了三角形、四边形、 圆及图形的变换。其中三角形知识点考查面广,如三角形的 性质(第6题)、全等三角形的性质与判定(第23题)、 相似三角形的性质与判定(第9、10、22题)、等腰三角形 的性质(第22题)、直角三角形的性质及解直角三角形(第 13、19题);四边形知识点的考查较综合(第5、6、9题), 圆的知识考查了垂径定理(第13题)、圆周角定理及弧长 公式(第7题);图形变换考查了旋转、平移、位似(第17、 22题). 其次,试题延续2010年的平稳趋势,严格按照考纲出 题,试题难易适中,没有出现“怪、偏、繁”题,试卷难题 分布合适.如第21题、22题和23题考查了几何推理能力和 数学综合分析能力,对学生数学思维能力的考查很全面。第 21题是把一次函数与反比例相结合,使二次函数融合在几何
题共 10 道题,每题 4 分;填空题 4 道题,每题 5 分;最后 三道题分值分别为 12 分、12 分、14 分.代数部分约占 48%, 几何部分约占 52%.其中代数部分对基础知识和基本能力的 考查,如简单的实数大小比较(第 1 题)、科学记数法(第 2 题)、分式化简(第 15 题)、一元二次方程的解法(第 8 题)、一元一次方程的应用(第 16 题)、新定义运算(第 2、 14 题);函数部分考查了一次函数与反比例函数的图像和性 质(第 21 题)、二次函数的增减性(第 23 题的 3 问)及统 计与概率(第 5、20 题).几何部分考查了三角形、四边形、 圆及图形的变换。其中三角形知识点考查面广,如三角形的 性质(第 6 题)、全等三角形的性质与判定(第 23 题)、 相似三角形的性质与判定(第 9、10、22 题)、等腰三角形 的性质(第 22 题)、直角三角形的性质及解直角三角形(第 13、19 题);四边形知识点的考查较综合(第 5、6、9 题), 圆的知识考查了垂径定理(第 13 题)、圆周角定理及弧长 公式(第 7 题);图形变换考查了旋转、平移、位似(第 17、 22 题). 其次,试题延续 2010 年的平稳趋势,严格按照考纲出 题,试题难易适中,没有出现“怪、偏、繁”题,试卷难题 分布合适.如第 21 题、22 题和 23 题考查了几何推理能力和 数学综合分析能力,对学生数学思维能力的考查很全面。第 21 题是把一次函数与反比例相结合,使二次函数融合在几何

题中,既淡化了这类考题的分量,同时又能考查考生的综合 能力,命题思路较好.第22题是几何图形的旋转问题,在 旋转中找角的度数,线段之间的关系,题目没有突破常规, 但是延续了学生在解数学题中的思维难点,让学生“够一够 能抓到”,是一道训练思考能力和思想方法的好几何题。第 23题,是在一个基本几何图形框架下考查全等三角形及二次 函数的问题,是一道代数与几何相结合的好题. 此外,试卷新增了规律探索题、淡化了概率的运用、二 次函数和一次函数的应用等中考热点问题.规律探索题是安 徽省中考命题的一大特色,在前几年中考中有着很重的分 量,但是2009、2010年的考题基本上是把规律探索题放在 选择和填空中,而2011年的考题则加大了规律探索题的分 量,且出现在大题中,很明显,这是着重对数学能力的考查, 纵观以上试题结构,不难发现,试题仍以考查学生的基 本知识与基本能力为主,但考查知识点偏重于几何部分,以 凸显学生的逻辑思维能力,其中第9、10、22题的第(3) 问有一定的区分度.最明显的是,2011年安徽省中考数学的 阅读理解题能较好地考查学生的阅读理解能力与日常生活 体验,同时又能考查学生获取信息后的抽象概括能力、建模 能力、决策判断能力,是一大亮点.如第12、14、18、20 题,试题背景考生较熟悉,很容易入手,问题设置有创新、 有变化也是2011年命题的一大特点
题中,既淡化了这类考题的分量,同时又能考查考生的综合 能力,命题思路较好.第 22 题是几何图形的旋转问题,在 旋转中找角的度数,线段之间的关系,题目没有突破常规, 但是延续了学生在解数学题中的思维难点,让学生“够一够 能抓到”,是一道训练思考能力和思想方法的好几何题。第 23 题,是在一个基本几何图形框架下考查全等三角形及二次 函数的问题,是一道代数与几何相结合的好题. 此外,试卷新增了规律探索题、淡化了概率的运用、二 次函数和一次函数的应用等中考热点问题.规律探索题是安 徽省中考命题的一大特色,在前几年中考中有着很重的分 量,但是 2009、2010 年的考题基本上是把规律探索题放在 选择和填空中,而 2011 年的考题则加大了规律探索题的分 量,且出现在大题中,很明显,这是着重对数学能力的考查. 纵观以上试题结构,不难发现,试题仍以考查学生的基 本知识与基本能力为主,但考查知识点偏重于几何部分,以 凸显学生的逻辑思维能力,其中第 9、10、22 题的第(3) 问有一定的区分度.最明显的是,2011 年安徽省中考数学的 阅读理解题能较好地考查学生的阅读理解能力与日常生活 体验,同时又能考查学生获取信息后的抽象概括能力、建模 能力、决策判断能力,是一大亮点.如第 12、14、18、20 题,试题背景考生较熟悉,很容易入手,问题设置有创新、 有变化也是 2011 年命题的一大特点.

【考题再现】: 例1(2011安徽省中考数学第9题)如图1,在四边形 ABCD中,∠BAD=∠ADC=90°,AB=AD=22,CD=V2 点P在四边形ABCD的边上.若点P到BD的距离为2,则 点P的个数为() A.1B.2C.3 D.4 用1 解析:选B。分别过A、C两点作AE⊥BD于E,CFI BD于F,由勾股定理得BD=4,从△ABD的面积计算可得 AB·AD=AE·BD,AE=2,点P到BD的距离为2,因此, 在边AD、AB上可以分别找到一个点P;而CE<CD,即CE<2, 亦即82,所以,在边BC、CD上均找不到点P,综上符 合条件的点P的个数只有两个,分别在边AD、AB上各 个. 点评:此题设题较为简明,思考方法灵活,体现了由一般 到特殊的命题特色,能较好地引导学生掌握从一般到特殊的 思想方法
【考题再现】: 例 1(2011 安徽省中考数学第 9 题)如图 1,在四边形 ABCD 中,∠BAD=∠ADC=90°,AB=AD= ,CD= , 点 P 在四边形 ABCD 的边上.若点 P 到 BD 的距离为 ,则 点 P 的个数为( ) A.1 B.2 C.3 D.4 解析:选 B。分别过 A、C 两点作 AE⊥BD 于 E,CF⊥ BD 于 F,由勾股定理得 BD=4,从△ABD 的面积计算可得 AB·AD=AE·BD,AE=2,点 P 到 BD 的距离为 ,因此, 在边 AD、AB 上可以分别找到一个点 P;而 ,即 , 亦即 ,所以,在边 BC、CD 上均找不到点 P;综上符 合条件的点 P 的个数只有两个,分别在边 AD、AB 上各一 个. 点评:此题设题较为简明,思考方法灵活,体现了由一般 到特殊的命题特色,能较好地引导学生掌握从一般到特殊的 思想方法.

例2(2011安徽省中考数学第10题)如图2,点P是 菱形ABCD的对角线AC上的一个动点,过点P垂直于AC 的直线交菱形ABCD的边于M、N两点. 图2 设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于 x的函数图象大致形状是() 解析:选C。点P在AC的左半边移动时,即0<x<1时, w,则W,即-,当点P在AC的右半边移 动时即1<x<2时,w2-,则-号0,即=+, 综上,选C. 点评:此题图形较为美观,包含了很多几何、代数知识, 能真正考查学生的数形结合思想方法及计算能力,但笔者在 中考阅卷中也发现这样的问题:当点P在AC的左半边移动 时,即0<<1时,多数考生都可以得到函数的解析式, 当点P在AC的右半边移动时,即1<x<2时,不少考生产生 困难,难以得到函数解析式+“,从而难以在B、C两
例 2(2011 安徽省中考数学第 10 题)如图 2,点 P 是 菱形 ABCD 的对角线 AC 上的一个动点,过点 P 垂直于 AC 的直线交菱形 ABCD 的边于 M、N 两点. 设 , , ,△AMN 的面积为 ,则 关于 的函数图象大致形状是( ) 解析:选 C。点 P 在 AC 的左半边移动时,即 时, ,则 ,即 ;当点 P 在 AC 的右半边移 动时,即 时, ,则 ,即 , 综上,选 C. 点评:此题图形较为美观,包含了很多几何、代数知识, 能真正考查学生的数形结合思想方法及计算能力.但笔者在 中考阅卷中也发现这样的问题:当点 P 在 AC 的左半边移动 时,即 时,多数考生都可以得到函数的解析式 ; 当点 P 在 AC 的右半边移动时,即 时,不少考生产生 困难,难以得到函数解析式 ,从而难以在 B、C 两

个选项中抉择,这反映出有些考生计算能力差的弱点,数形 结合思想体会也不够深。 例3(2011安徽省中考数学第18题)在平面直角坐标系 中,一蚂蚁从原点0出发,按向上、向右、向下、向右的方 向依次不断移动,每次移动1个单位,其行走路线如图3所 示. 图3 )填写下列各点的坐标:A4(一,As一,—、 A12(,); (2)写出点A4m的坐标(n是正整数); (3)指出蚂蚁从点A10到点A101的移动方向. 解析:(1)A4(2,0)、As(4,0)、 A12(6,0); (2)A4n=(2n,0_)· 易得规律为:每4步,则向右行进两个单位长度,因此 横坐标为2,且第四步都回到x轴,因此纵坐标为0. (3)向上.因为100是4的倍数,因此A10到点A101的 移动方向与点A4到点4的移动方向相同
个选项中抉择,这反映出有些考生计算能力差的弱点,数形 结合思想体会也不够深. 例 3(2011 安徽省中考数学第 18 题)在平面直角坐标系 中,一蚂蚁从原点 O 出发,按向上、向右、向下、向右的方 向依次不断移动,每次移动 1 个单位,其行走路线如图 3 所 示. (1)填写下列各点的坐标:A4( , )、A8( , )、 A12( , ); (2)写出点 A4n 的坐标(n 是正整数); (3)指出蚂蚁从点 A100 到点 A101 的移动方向. 解析: ( 1 ) A4( 2 , 0 )、 A8( 4 , 0 )、 A12( 6 , 0 ); (2)A4n=( 2n , 0 ) . 易得规律为:每 4 步,则向右行进两个单位长度,因此 横坐标为 2n,且第四步都回到 轴,因此纵坐标为 0. (3)向上.因为 100 是 4 的倍数,因此 A100到点 A101的 移动方向与点 A4 到点 的移动方向相同.
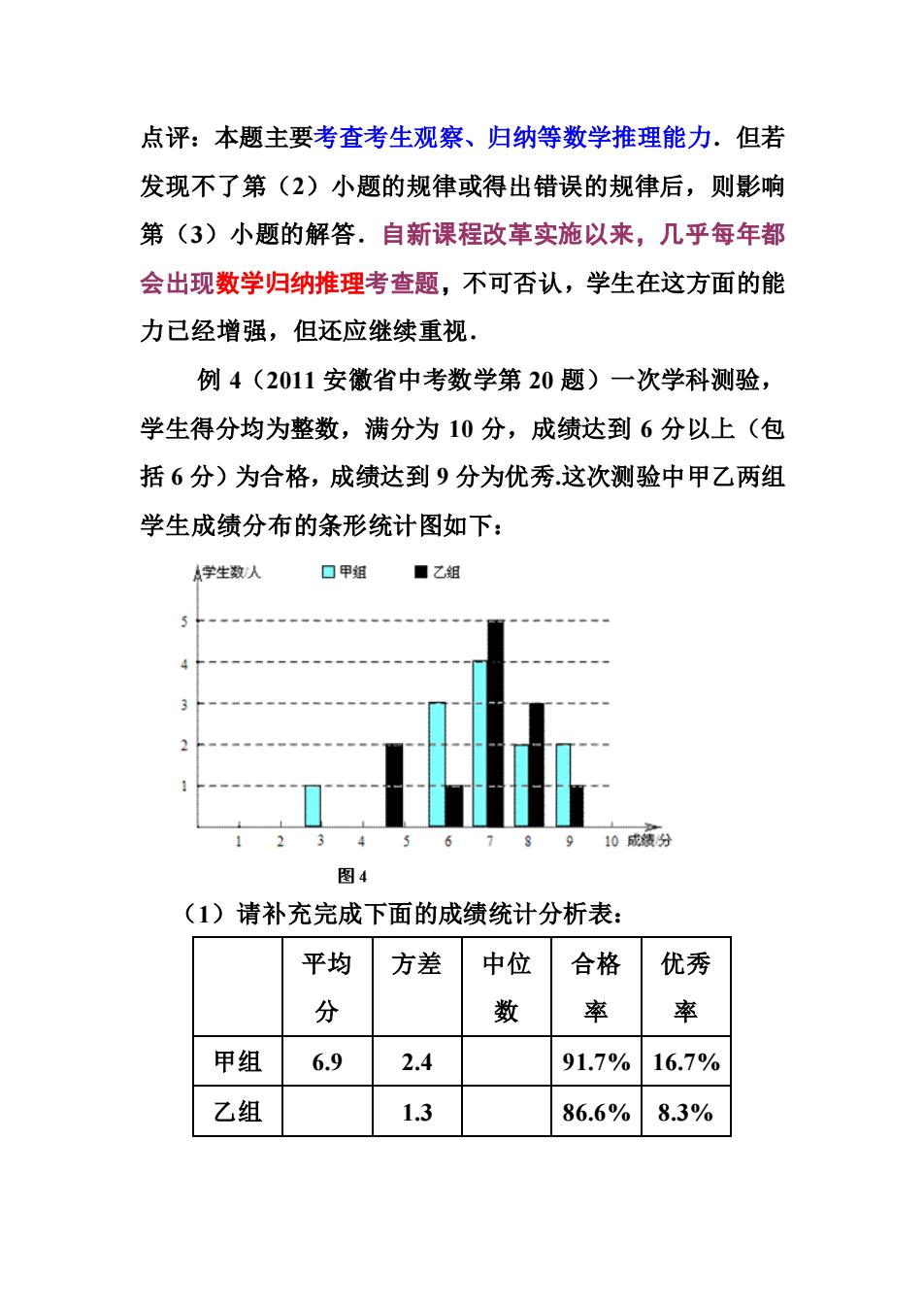
点评:本题主要考查考生观察、归纳等数学推理能力.但若 发现不了第(2)小题的规律或得出错误的规律后,则影响 第(3)小题的解答.自新课程改革实施以来,几乎每年都 会出现数学归纳推理考查题,不可否认,学生在这方面的能 力已经增强,但还应继续重视. 例4(2011安徽省中考数学第20题)一次学科测验, 学生得分均为整数,满分为10分,成绩达到6分以上(包 括6分)为合格,成绩达到9分为优秀这次测验中甲乙两组 学生成绩分布的条形统计图如下: A学生数人 口甲组 ■乙组 10成 图4 (1)请补充完成下面的成绩统计分析表: 平均 方差 中位 合格 优秀 文 数 率 甲组 6.9 2.4 91.7%16.7% 乙组 1.3 86.6%8.3%
点评:本题主要考查考生观察、归纳等数学推理能力.但若 发现不了第(2)小题的规律或得出错误的规律后,则影响 第(3)小题的解答.自新课程改革实施以来,几乎每年都 会出现数学归纳推理考查题,不可否认,学生在这方面的能 力已经增强,但还应继续重视. 例 4(2011 安徽省中考数学第 20 题)一次学科测验, 学生得分均为整数,满分为 10 分,成绩达到 6 分以上(包 括 6 分)为合格,成绩达到 9 分为优秀.这次测验中甲乙两组 学生成绩分布的条形统计图如下: (1)请补充完成下面的成绩统计分析表: 平均 分 方差 中位 数 合格 率 优秀 率 甲组 6.9 2.4 91.7% 16.7% 乙组 1.3 86.6% 8.3%

(2)甲组学生说他们的合格率、优秀率均高于乙组,所 以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法, 认为他们组的成绩要好于甲组,请你给出三条支持乙组学生 观点的理由 解析:(1) 平均 方差 中位 合格 优秀 分 数 率 率 甲组 6.9 2.4 7 91.7%16.7% 乙组 2 1.3 7 86.6%8.3% (2)①乙组的平均分比甲组高: ②乙组的方差比甲组小; ③乙组学生成绩不低于7分的人数比甲组多 点评:本题属于基础考查题,但在阅卷中发现考生出现 的典型错误是:乙组学生成绩7分以上的人数比甲组多,本 题由完成成绩统计分析表出发,到探究分析乙组学生不同意 甲组学生说法的原因,进而给出三条支持乙组学生观点的理 由,由浅入深,无形之中,既照顾到不同层次的学生,又含 有乐趣。这是科学研究、科学探究的重要方法.这种研究、 思维模式对学生是十分有益的.学生自我探究后,既有成就 感,增强自信心,又可有效地改善、提升思维水平
(2)甲组学生说他们的合格率、优秀率均高于乙组,所 以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法, 认为他们组的成绩要好于甲组,请你给出三条支持乙组学生 观点的理由. 解析:(1) 平均 分 方差 中位 数 合格 率 优秀 率 甲组 6.9 2.4 7 91.7% 16.7% 乙组 7 1.3 7 86.6% 8.3% (2)①乙组的平均分比甲组高; ②乙组的方差比甲组小; ③乙组学生成绩不低于 7 分的人数比甲组多. 点评:本题属于基础考查题,但在阅卷中发现考生出现 的典型错误是:乙组学生成绩 7 分以上的人数比甲组多.本 题由完成成绩统计分析表出发,到探究分析乙组学生不同意 甲组学生说法的原因,进而给出三条支持乙组学生观点的理 由,由浅入深,无形之中,既照顾到不同层次的学生,又含 有乐趣。这是科学研究、科学探究的重要方法.这种研究、 思维模式对学生是十分有益的.学生自我探究后,既有成就 感,增强自信心,又可有效地改善、提升思维水平.
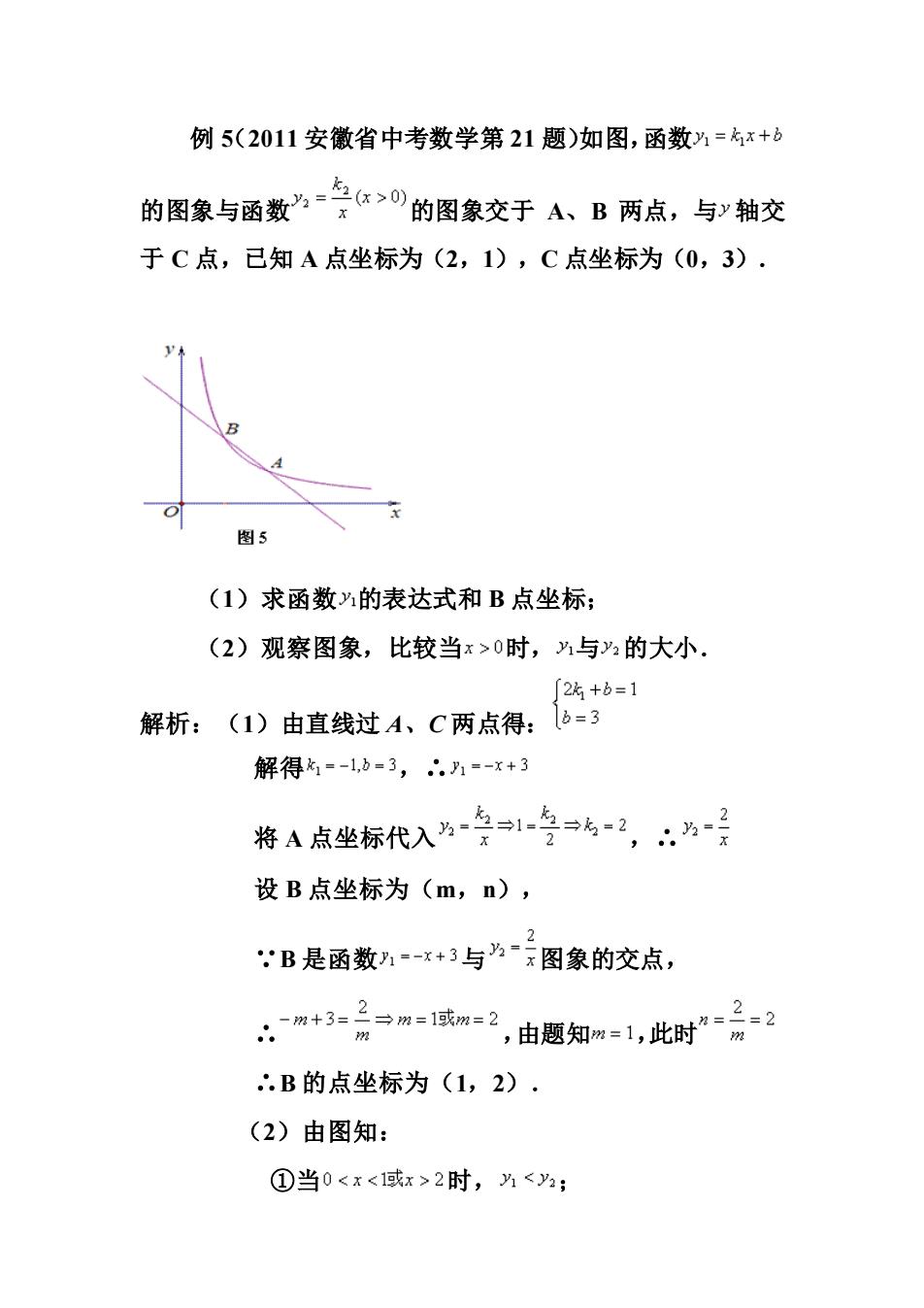
例5(2011安徽省中考数学第21题)如图,函数为=x+b 的图象与函数=兰:>的图象交于A、B两点,与》轴交 于C点,已知A点坐标为(2,1),C点坐标为(0,3). (1)求函数的表达式和B点坐标; (2)观察图象,比较当x>0时,与2的大小 「2%+b=1 解析:(1)由直线过A、C两点得:b=3 解得=-1,b=3,.1=-x+3 将A点坐标代入为兰1营%,:为层 2 设B点坐标为(m,n), :B是函数-x+3与为图象的交点, 、加+3=品宁m=减=2,由题知m,此时后2 .B的点坐标为(1,2). (2)由图知: ①当02时,乃<;
例 5(2011 安徽省中考数学第 21 题)如图,函数 的图象与函数 的图象交于 A、B 两点,与 轴交 于 C 点,已知 A 点坐标为(2,1),C 点坐标为(0,3). (1)求函数 的表达式和 B 点坐标; (2)观察图象,比较当 时, 与 的大小. 解析:(1)由直线过 A、C 两点得: 解得 ,∴ 将 A 点坐标代入 ,∴ 设 B 点坐标为(m,n), ∵B 是函数 与 图象的交点, ∴ ,由题知 ,此时 ∴B 的点坐标为(1,2). (2)由图知: ①当 时, ;

②当0=1或x=2时,片=: ③当1. 点评:本题属于基础考查题,难度适中,重视基础知识 和基本技能的应用.试题立足于学生发展,体现出人文关怀, 既考查了基础知识、基本技能和基本数学思想方法的掌握情 况,又考查了学生的基本运算能力、思维能力、创新能力、 实践能力,是一道极富思维含量的好题.此题命题意图明确, 充分体现出数学学科的应用价值,这对引导学生认清数学知 识的本质以及引领初中数学教与学方面都有着较好的导向 作用. 例6(2011安徽省中考数学第22题)在△ABC中,∠ ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转, 旋转角为0°<8<180°(0°<9<180),得到△A1B1C. 图6-1 图62 图63 (1)如图1,当AB∥CB1时,设AB1与BC相交于点D.证 明:△A1CD是等边三角形;
②当 时, ; ③当 时, . 点评:本题属于基础考查题,难度适中,重视基础知识 和基本技能的应用.试题立足于学生发展,体现出人文关怀, 既考查了基础知识、基本技能和基本数学思想方法的掌握情 况,又考查了学生的基本运算能力、思维能力、创新能力、 实践能力,是一道极富思维含量的好题.此题命题意图明确, 充分体现出数学学科的应用价值,这对引导学生认清数学知 识的本质以及引领初中数学教与学方面都有着较好的导向 作用. 例 6(2011 安徽省中考数学第 22 题)在△ABC 中,∠ ACB ,∠ABC ,将△ABC 绕顶点 C 顺时针旋转, 旋转角为 ( ),得到△A1B1C. (1)如图 1,当 AB∥CB1时,设 A1B1与 BC相交于点 D.证 明:△A1CD 是等边三角形;