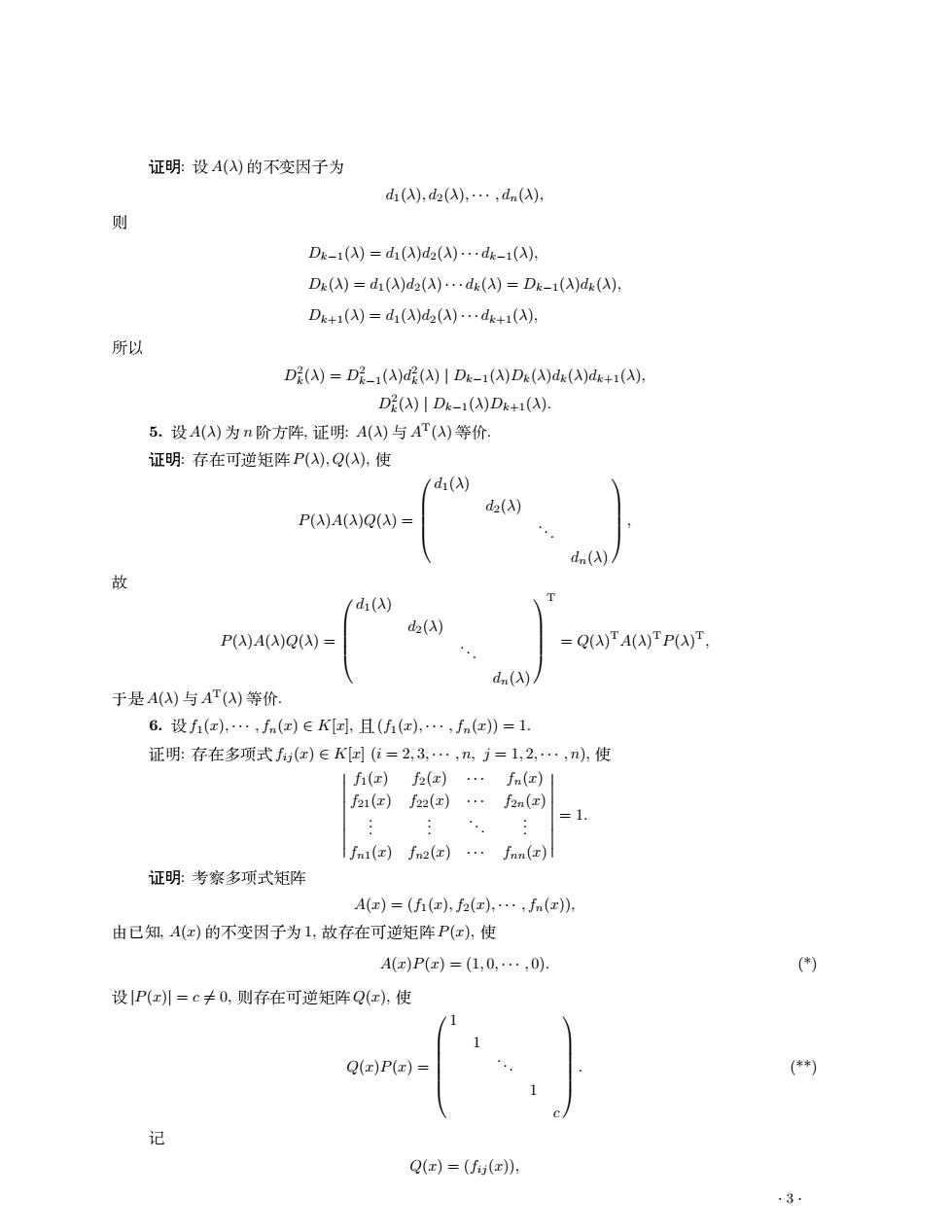
证明设A()的不变因子为 d(,d2(,,dn( Dk-1(A)=d(A)d2()…dk-1(A), Du(A)=di(A)da(X)...de(X)=Dg-1(A)d(), Dk+1()=d1(A)d2(A)…d+1(A, 所以 D2()=D2-1(A)(A)1Dk-1()Dk(A)d4(A)dk+1(A), Di(A)I D-1()D+(). 5.设A(A)为n阶方阵，证明A()与AT(A)等价 证明：存在可逆矩阵P(),Q(,使 /d() d() P(A)A(X)Q()= d() 故 d(A) d2(X) P()A()Q()- -Q(A)A(A)P(A)T. d.(A)/ 于是A(A)与AT(A)等价. 6.设fi(…,fn()∈K,且((,…,fn()=1. 证明：存在多项式f(x)∈K[(位=2,3，…，n,j=1,2,…,n),使 fi()f(z)…fn() n( =1. fn(）fn2(）…jnn(e) 证明：考察多项式矩阵 A(x)=(fi(x),fz(x).....fn(z)). 由已知，A(x)的不变因子为1，故存在可逆矩阵P(x,使 A(x)P(x)=(1,0,…,0) () 设P(x川-c≠0，则存在可逆矩阵Q(x,使 Q(z)P()= (*) 记 Q()-(j() 3 NO: A(λ)  l d1(λ), d2(λ), · · · , dn(λ), = Dk−1(λ) = d1(λ)d2(λ)· · · dk−1(λ), Dk(λ) = d1(λ)d2(λ)· · · dk(λ) = Dk−1(λ)dk(λ), Dk+1(λ) = d1(λ)d2(λ)· · · dk+1(λ), H D2 k (λ) = D2 k−1 (λ)d 2 k (λ) | Dk−1(λ)Dk(λ)dk(λ)dk+1(λ), D2 k (λ) | Dk−1(λ)Dk+1(λ). 5. A(λ) l n
?", 01: A(λ)  AT(λ) T. NO: m%3M!" P(λ), Q(λ), < P(λ)A(λ)Q(λ) =   d1(λ) d2(λ) . . . dn(λ)   ,  P(λ)A(λ)Q(λ) =   d1(λ) d2(λ) . . . dn(λ)   T = Q(λ) TA(λ) TP(λ) T, L# A(λ)  AT(λ) T. 6. f1(x), · · · , fn(x) ∈ K[x], b (f1(x), · · · , fn(x)) = 1. 01: m% fij (x) ∈ K[x] (i = 2, 3, · · · , n, j = 1, 2, · · · , n), < ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ f1(x) f2(x) · · · fn(x) f21(x) f22(x) · · · f2n(x) . . . . . . . . . . . . fn1(x) fn2(x) · · · fnn(x) ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ = 1. NO:  !" A(x) = (f1(x), f2(x), · · · , fn(x)),  , A(x)  l 1, m%3M!" P(x), < A(x)P(x) = (1, 0, · · · , 0). (*) |P(x)| = c 6= 0, =m%3M!" Q(x), < Q(x)P(x) =   1 1 . . . 1 c   . (**)  Q(x) = (fij (x)), · 3 ·