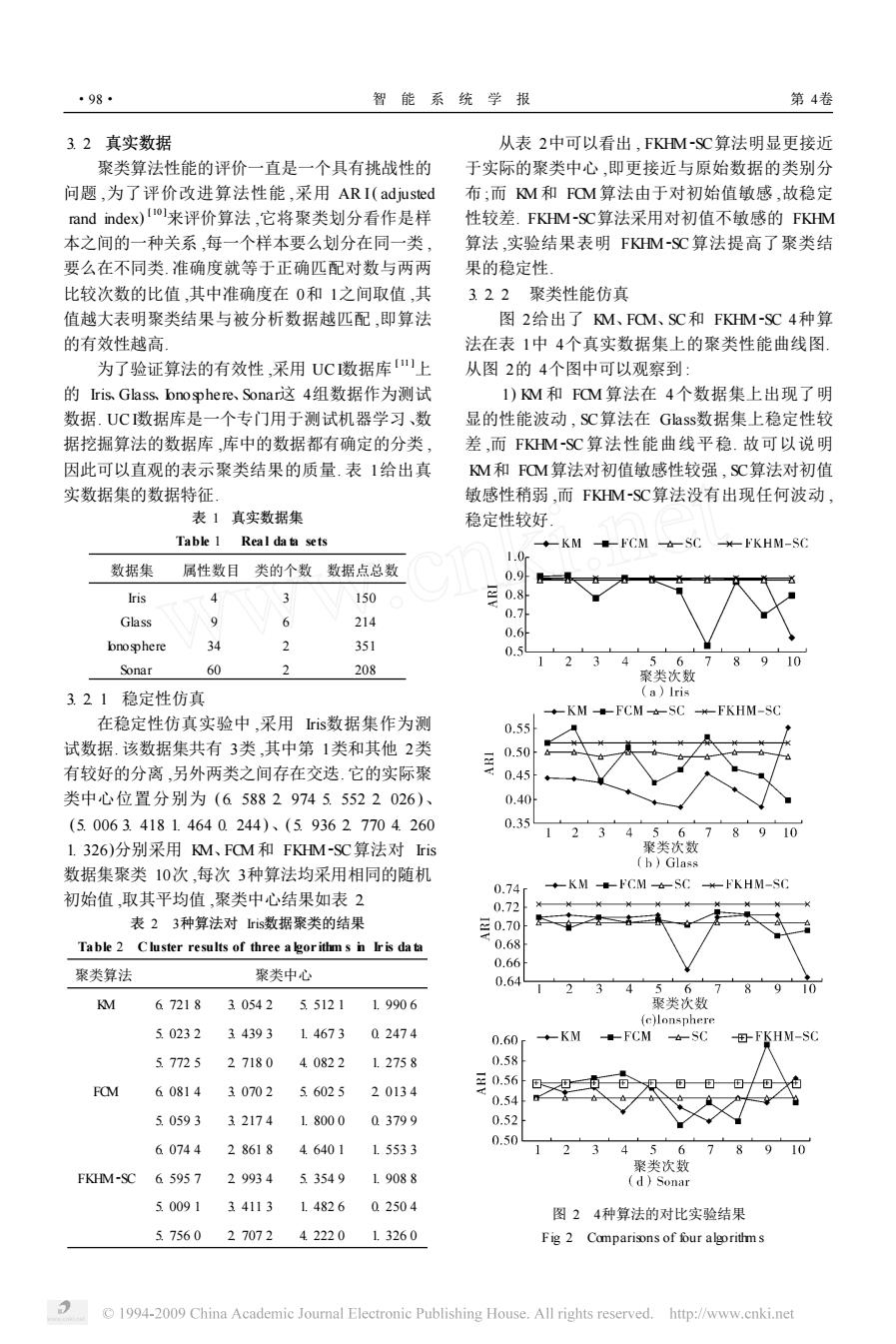
·98* 智能系统学报 第4卷 3.2真实数据 从表2中可以看出，FKM-SC算法明显更接近 聚类算法性能的评价一直是一个具有挑战性的 于实际的聚类中心，即更接近与原始数据的类别分 问题，为了评价改进算法性能，采用ARI(adjusted 布；而M和FQM算法由于对初始值敏感，故稳定 rand index)iol来评价算法，它将聚类划分看作是样 性较差.FKHM-SC算法采用对初值不敏感的FKHM 本之间的一种关系，每一个样本要么划分在同一类， 算法，实验结果表明FIM-SC算法提高了聚类结 要么在不同类.准确度就等于正确匹配对数与两两 果的稳定性。 比较次数的比值，其中准确度在0和1之间取值，其 322聚类性能仿真 值越大表明聚类结果与被分析数据越匹配，即算法 图2给出了M、FQM、SC和FKHM-SC4种算 的有效性越高】 法在表1中4个真实数据集上的聚类性能曲线图， 为了验证算法的有效性，采用UC数据库1上 从图2的4个图中可以观察到： 的ris.Gass、bnosphere.Sonari这4组数据作为测试 1)M和FQM算法在4个数据集上出现了明 数据.UC数据库是一个专门用于测试机器学习、数 显的性能波动，SC算法在Glass数据集上稳定性较 据挖掘算法的数据库，库中的数据都有确定的分类， 差，而FKM-SC算法性能曲线平稳.故可以说明 因此可以直观的表示聚类结果的质量.表1给出真 M和FOM算法对初值敏感性较强，SC算法对初值 实数据集的数据特征」 敏感性稍弱，而FIHM-SC算法没有出现任何波动， 表1真实数据集 稳定性较好 Table 1 Real data sets ◆-KM■-CM-SC-'KHM-SC 1.0r 数据集 属性数目类的个数数据点总数 0.9外 Iris 4 3 150 三0.8 Glass 9 6 0.7 214 0.6 bnosphere 34 2 351 0.5 1 4 56 Sonar 60 2 208 聚类次数 3.21稳定性仿真 (a）lris ◆KM--FCM-SCW-FKHM-SC 在稳定性仿真实验中，采用is数据集作为测 0.55 试数据.该数据集共有3类，其中第1类和其他2类 0.50 有较好的分离，另外两类之间存在交迭.它的实际聚 0.45 类中心位置分别为(6588297455522026)、 0.40 (5.0063.41814640244)、(5.93627704260 0.35 5 6 8 10 1.326)分别采用M、FQM和FKHM-SC算法对ris 聚类次数 (h)Glass 数据集聚类10次，每次3种算法均采用相同的随机 0.74 ◆KM■-FCM女-SC#kKHM-SG 初始值，取其平均值，聚类中心结果如表2 0.72 表23种算法对is数据聚类的结果 三0.70 Table 2 Cluster results of three a lgorithm s n Ir is da ta 0.68 0.66 聚类算法 聚类中心 0.64 6 M 67218 30542 5.5121 1.9906 聚类次数 (c)lonsphere 50232 34393 1.4673 02474 0.60 ◆-KM ■-FCM SC -FKHM-SC 57725 27180 40822 1.2758 0.58 FOM 60814 30702 5.6025 20134 年056 0.54 50593 321741.8000 03799 0.52 0.50 60744 28618 46401 1.5533 4 5 6 7 8 910 聚类次数 FKHM-SC 65957 2993453549 1.9088 (d)Sonar 50091341131.482602504 图24种算法的对比实验结果 5.756027072 42220 1.3260 Fig 2 Comparisons of four algorithms 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net3. 2 真实数据 聚类算法性能的评价一直是一个具有挑战性的 问题 ,为了评价改进算法性能 ,采用 AR I( adjusted rand index) [ 10 ]来评价算法 ,它将聚类划分看作是样 本之间的一种关系 ,每一个样本要么划分在同一类 , 要么在不同类. 准确度就等于正确匹配对数与两两 比较次数的比值 ,其中准确度在 0和 1之间取值 ,其 值越大表明聚类结果与被分析数据越匹配 ,即算法 的有效性越高. 为了验证算法的有效性 ,采用 UC I数据库 [ 11 ]上 的 Iris、Glass、Ionosphere、Sonar这 4组数据作为测试 数据. UC I数据库是一个专门用于测试机器学习、数 据挖掘算法的数据库 ,库中的数据都有确定的分类 , 因此可以直观的表示聚类结果的质量. 表 1给出真 实数据集的数据特征. 表 1 真实数据集 Table 1 Rea l da ta sets 数据集 属性数目 类的个数 数据点总数 Iris 4 3 150 Glass 9 6 214 Ionosphere 34 2 351 Sonar 60 2 208 3. 2. 1 稳定性仿真 在稳定性仿真实验中 ,采用 Iris数据集作为测 试数据. 该数据集共有 3类 ,其中第 1类和其他 2类 有较好的分离 ,另外两类之间存在交迭. 它的实际聚 类中心位置分别为 ( 6. 588 2. 974 5. 552 2. 026 )、 (5. 006 3. 418 1. 464 0. 244 )、( 5. 936 2. 770 4. 260 1. 326)分别采用 KM、FCM和 FKHM2SC算法对 Iris 数据集聚类 10次 ,每次 3种算法均采用相同的随机 初始值 ,取其平均值 ,聚类中心结果如表 2. 表 2 3种算法对 Iris数据聚类的结果 Table 2 C luster results of three a lgor ithm s in Ir is da ta 聚类算法 聚类中心 KM 6. 721 8 3. 054 2 5. 512 1 1. 990 6 5. 023 2 3. 439 3 1. 467 3 0. 247 4 5. 772 5 2. 718 0 4. 082 2 1. 275 8 FCM 6. 081 4 3. 070 2 5. 602 5 2. 013 4 5. 059 3 3. 217 4 1. 800 0 0. 379 9 6. 074 4 2. 861 8 4. 640 1 1. 553 3 FKHM2SC 6. 595 7 2. 993 4 5. 354 9 1. 908 8 5. 009 1 3. 411 3 1. 482 6 0. 250 4 5. 756 0 2. 707 2 4. 222 0 1. 326 0 从表 2中可以看出 , FKHM2SC算法明显更接近 于实际的聚类中心 ,即更接近与原始数据的类别分 布 ;而 KM 和 FCM算法由于对初始值敏感 ,故稳定 性较差. FKHM2SC算法采用对初值不敏感的 FKHM 算法 ,实验结果表明 FKHM2SC算法提高了聚类结 果的稳定性. 3. 2. 2 聚类性能仿真 图 2给出了 KM、FCM、SC和 FKHM2SC 4种算 法在表 1中 4个真实数据集上的聚类性能曲线图. 从图 2的 4个图中可以观察到 : 1) KM 和 FCM 算法在 4个数据集上出现了明 显的性能波动 , SC算法在 Glass数据集上稳定性较 差 ,而 FKHM2SC算法性能曲线平稳. 故可以说明 KM和 FCM算法对初值敏感性较强 , SC算法对初值 敏感性稍弱 ,而 FKHM2SC算法没有出现任何波动 , 稳定性较好. 图 2 4种算法的对比实验结果 Fig. 2 Comparisons of four algorithm s ·98· 智 能 系 统 学 报 第 4卷