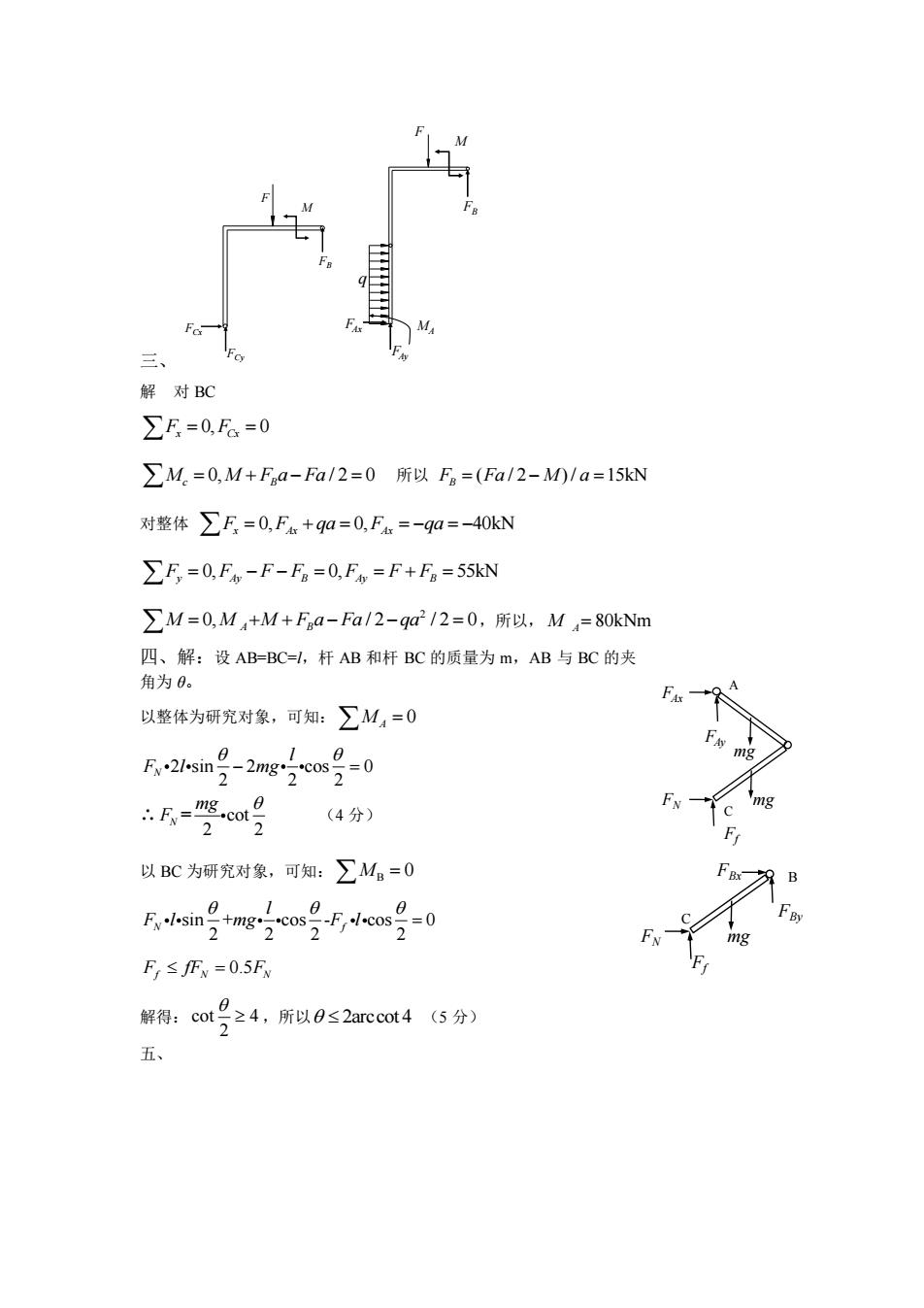
三、 解对BC ∑F=0,a=0 ∑M.=0,M+Faa-Fa/2=0所以Fg=(Fa/2-M0/a=l5kN 对整体∑F=0,F+q0=0,Fa=-qa=-40kN >F=0.Fo-F-Fn=0,Fo=F+Fn=55kN ∑M=0,M+M+Faa-Fa/2-qa2/2=0,所以，MA=80kNm 四、解：设AB=BC=l,杆AB和杆BC的质量为m,AB与BC的夹 角为0。 以整体为研究对象，可知：∑M4=0 rsn号-2ngom号=0 F划 “F="m8cot号 mg (4分) FN 2 F 以BC为研究对象，可知：∑M。=0 B 10 Fl.sintmgcosFcos=0 2 2 2 mg F,≤Fw=0.5Fw 解得：cot9≥4，所以0≤2 arccot4(5分) 五、三、 M F FB FCy FCx F M FB q FAy FAx MA 解 对 BC 0, 0 F F x Cx = = 0, / 2 0 M M F a Fa c B = + − = 所以 F Fa M a B = − = ( / 2 ) / 15kN 对整体 F F qa F qa x Ax Ax = + = = − = − 0, 0, 40kN F F F F F F F y Ay B Ay B = − − = = + = 0, 0, 55kN 2 0, / 2 / 2 0 M M M F a Fa qa = + + − − = A B ，所以， M A = 80kNm 四、解：设 AB=BC=l，杆 AB 和杆 BC 的质量为 m，AB 与 BC 的夹 角为 θ。 以整体为研究对象，可知： 0 MA = 2 sin 2 cos 0 2 2 2 N l F l mg   − = ∴ = cot 2 2 N mg F  （4 分） 以 BC 为研究对象，可知： B M = 0 sin + cos - cos 0 2 2 2 2 N f l F l mg F l    = 0.5 F fF F f N N  = 解得： cot 4 2   ，所以   2arccot 4 （5 分） 五、 C A FAx FAy FN Ff mg mg C FN Ff B FBy FBx mg