
佛山科学技术学院2017~2018学年第二学期 《理论力学》课程期末考试试题解答及评分标准(C) 专业、班级:土木工程系任课教师:罗冬梅、陈舟、王英涛 一.选择题,每题2分,共10分 1、B,2、C,3、A,4、D,5、C 二、(1)解: FBA F AB (2)解:向点0简化, Fo=-v2. -N 2 =1+V2.2 =2N F=-3N 所以F(i+2j-3k)N,F=√层+F%+F=V④N(4分) M,--xxl+3xI)a=-4aN.m M,-(3x1-ExxIa-2aNom M.=(lx1+xxDa=2aNom 所以M=(-4ai+2ag+2ak)Nm,M=√M+MG+M=24aNm(5分)
佛山科学技术学院 2017~2018 学年第 二 学期 《理论力学》课程期末考试试题解答及评分标准 (C) 专业、班级: 土木工程系 任课教师:罗冬梅、陈舟、王英涛 一.选择题,每题 2 分,共 10 分 1、B, 2、C, 3、A,4、D, 5、C 二、(1)解: F FAB FBA F’ F’ AB C D A B C E F’BA FC FD FD (2)解:向点 O 简化, 2 - 2 1N 2 FRx = = − y 2 1 2 2N 2 FR = + = z FR = −3N 所以 FR =(-i+2j-3k)N, 2 2 2 F F F F R Rx Ry Rz = = 14N + + (4 分) 2 ( 2 1 3 1) 4 N m 2 M a a x = − + = − 2 (3 1 2 1) 2 N m 2 M a a y = − = z 2 (1 1 2 1) 2 N m 2 M a a = + = 所以 M ai aj ak = + + (-4 2 2 )N m , 222 M M M M a = + + x y z = 24 N m (5 分)
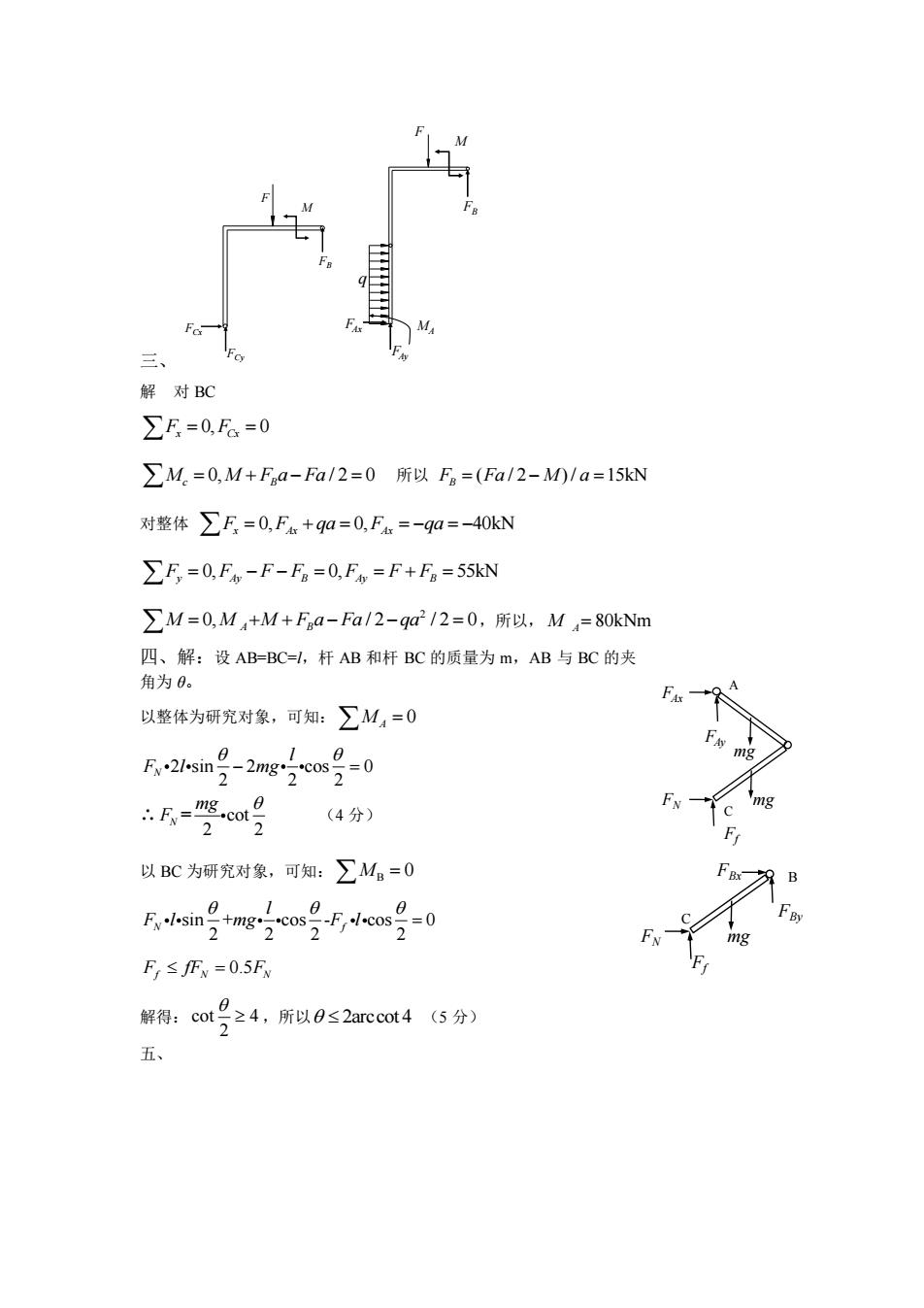
三、 解对BC ∑F=0,a=0 ∑M.=0,M+Faa-Fa/2=0所以Fg=(Fa/2-M0/a=l5kN 对整体∑F=0,F+q0=0,Fa=-qa=-40kN >F=0.Fo-F-Fn=0,Fo=F+Fn=55kN ∑M=0,M+M+Faa-Fa/2-qa2/2=0,所以,MA=80kNm 四、解:设AB=BC=l,杆AB和杆BC的质量为m,AB与BC的夹 角为0。 以整体为研究对象,可知:∑M4=0 rsn号-2ngom号=0 F划 “F="m8cot号 mg (4分) FN 2 F 以BC为研究对象,可知:∑M。=0 B 10 Fl.sintmgcosFcos=0 2 2 2 mg F,≤Fw=0.5Fw 解得:cot9≥4,所以0≤2 arccot4(5分) 五
三、 M F FB FCy FCx F M FB q FAy FAx MA 解 对 BC 0, 0 F F x Cx = = 0, / 2 0 M M F a Fa c B = + − = 所以 F Fa M a B = − = ( / 2 ) / 15kN 对整体 F F qa F qa x Ax Ax = + = = − = − 0, 0, 40kN F F F F F F F y Ay B Ay B = − − = = + = 0, 0, 55kN 2 0, / 2 / 2 0 M M M F a Fa qa = + + − − = A B ,所以, M A = 80kNm 四、解:设 AB=BC=l,杆 AB 和杆 BC 的质量为 m,AB 与 BC 的夹 角为 θ。 以整体为研究对象,可知: 0 MA = 2 sin 2 cos 0 2 2 2 N l F l mg − = ∴ = cot 2 2 N mg F (4 分) 以 BC 为研究对象,可知: B M = 0 sin + cos - cos 0 2 2 2 2 N f l F l mg F l = 0.5 F fF F f N N = 解得: cot 4 2 ,所以 2arccot 4 (5 分) 五、 C A FAx FAy FN Ff mg mg C FN Ff B FBy FBx mg

解以A点为动点,凸轮为动系 绝对运动为直线运动 相对运动为曲线运动 牵连运动为水平直线运动 v=V+V ∴v。=y.tanp=V5m。/3 y,=V./c0sp=2√5m,/3(5分) 又a。=a。+a+a 其中,g= R 式(a在n方向上投影: (5分) a,coso=a。sinp+a 代入数据,得 a2= 85+5 9R+3a (2分) 六、解:AB杆的瞬心在P点 (2分) Ve Ve 77777 (2分) D V V=PAXOAB,OAB lrad/s (2分)
B A o a a t r a n r a e a n (5 分) cos sin n a e r a a a = + 代入数据,得 2 0 8 3 3 9 3 a v a a R = + (2 分) 六、解: AB 杆的瞬心在 P 点 (2 分) (2 分) v PA rad s A AB AB = , =1 / (2 分) 解 以 A 点为动点,凸轮为动系 绝对运动为直线运动 相对运动为曲线运动 牵连运动为水平直线运动 0 0 tan 3 / 3 / cos 2 3 / 3 5 a e r a e r e v v v v v v = + = = = = ( 分) v v v 又 t n a a a a a e r r = + + 其中, 2 n r r v R a = 式 (a) 在 n 方向上投影:

Va Ve sin30°sin120°sin30° (2分) VB=PB×04B=0.2V3 (2分) 3 Va= 15 (CD杆的速度) (2分) (4分) 七、解:(1)质心的速度为:v= 6 杆AB的动量为p=mm=m (3分) (2)对0点的转动惯量,-mE+m2L-mc 12 6 9 1 杆AB的动量矩为L=J。w= gmL(3分) (3)杆AB的动能为 Tom2=mrEg分y 18 八、解:以整体为研究对象,画出系统的主动力如下: G01 12.r2 1712g P m 13g 根据各部分的运动形式,写出系统初始和末了的动能T和T2, 共5页第4页 系统初始静止,T=0 2y1=2r01=202= (1分) 5+m+5x2+m s1,1 11 m,(2r0,)2(3分) 2 =2m+2%+4m1ay 251
o r o e o a v v v sin 30 sin 120 sin 30 = = (2 分) vB = PBAB = 0.2 3 (2 分) 15 3 va = (CD 杆的速度) (2 分) (4 分) 七、解:(1)质心的速度为: 6 Lw v = 杆 AB 的动量为 6 mLw p mv = = (3 分) (2)对 O 点的转动惯量 1 1 1 2 2 2 ( ) 12 6 9 O J mL m L mL = + = 杆 AB 的动量矩为 1 2 9 L J w mwL = = O (3 分) (3)杆 AB 的动能为 1 1 2 2 2 2 18 T J w mw L = = O (3 分) 八、解:以整体为研究对象,画出系统的主动力如下: P ω1 ω1 v3 根据各部分的运动形式,写出系统初始和末了的动能 T1 和 T2, 共 5 页第 4 页 系统初始静止, 1 T = 0 1 1 1 2 2 3 2 2 v r r v = = = (1 分) 1 1 2 2 2 2 2 1 2 3 3 2 2 2 2 2 2 1 1 1 1 1 2 3 1 1 2 2 1 2 3 1 1 111 222 1 1 1 1 1 2 = ( ) ( )( ) (2 ) 2 2 2 2 2 1 3 = [ 2 4 ]( ) 2 2 T J J m v P B r m r m r m r m r r m m m r = + + + + + + + (3 分)

计算系统在整个运动过程中所有力所作的功,W=m,gh (2分) 由动能定理知:T,-T=W ·.2m+2m,+4m,1Go)=m,gh 22 2mgh 即2m+2m+4m=m,gh,人 3 2m+2m,+4m, 两边对时间求导,可得:a,= 2m38 (4分) 2m+2m,+4m, 以m3为研究对象, m3的加速度为a,=2a=3 4m38 (2分) m,+2m2+4m 2 根据质心的运动定理知: mg-T=mas 2m+2m,)m,8 ∴.T=m8-m3a3= 3 (3分) 2%+2m%+4m 共5页第5页
计算系统在整个运动过程中所有力所作的功, W m gh = 3 (2 分) 由动能定理知: T T W 2 1 − = ∴ 2 1 2 3 1 1 3 1 3[ 2 4 ]( ) = 2 2 m m m r m gh + + 即 2 1 2 3 1 3 1 3[ 2 4 ] = 2 2 m m m v m gh + + , 2 3 1 1 2 3 2 = 3 2 4 2 m gh v m m m + + 两边对时间求导,可得: 3 1 1 2 3 2 = 3 2 4 2 m g a m m m + + (4 分) 以 m3 为研究对象, m3 的加速度为 3 3 1 1 2 3 4 =2 = 3 2 4 2 m g a a m m m + + (2 分) 根据质心的运动定理知: m g T m a 3 3 3 − = ∴ 1 2 3 3 3 3 1 2 3 3 ( 2 ) 2 = 3 2 4 2 m m m g T m g m a m m m + = − + + (3 分) 共 5 页第 5 页