佛山科学技术学院：《土木理论力学》课程教学资源（试卷习题）理力试卷5（答案）

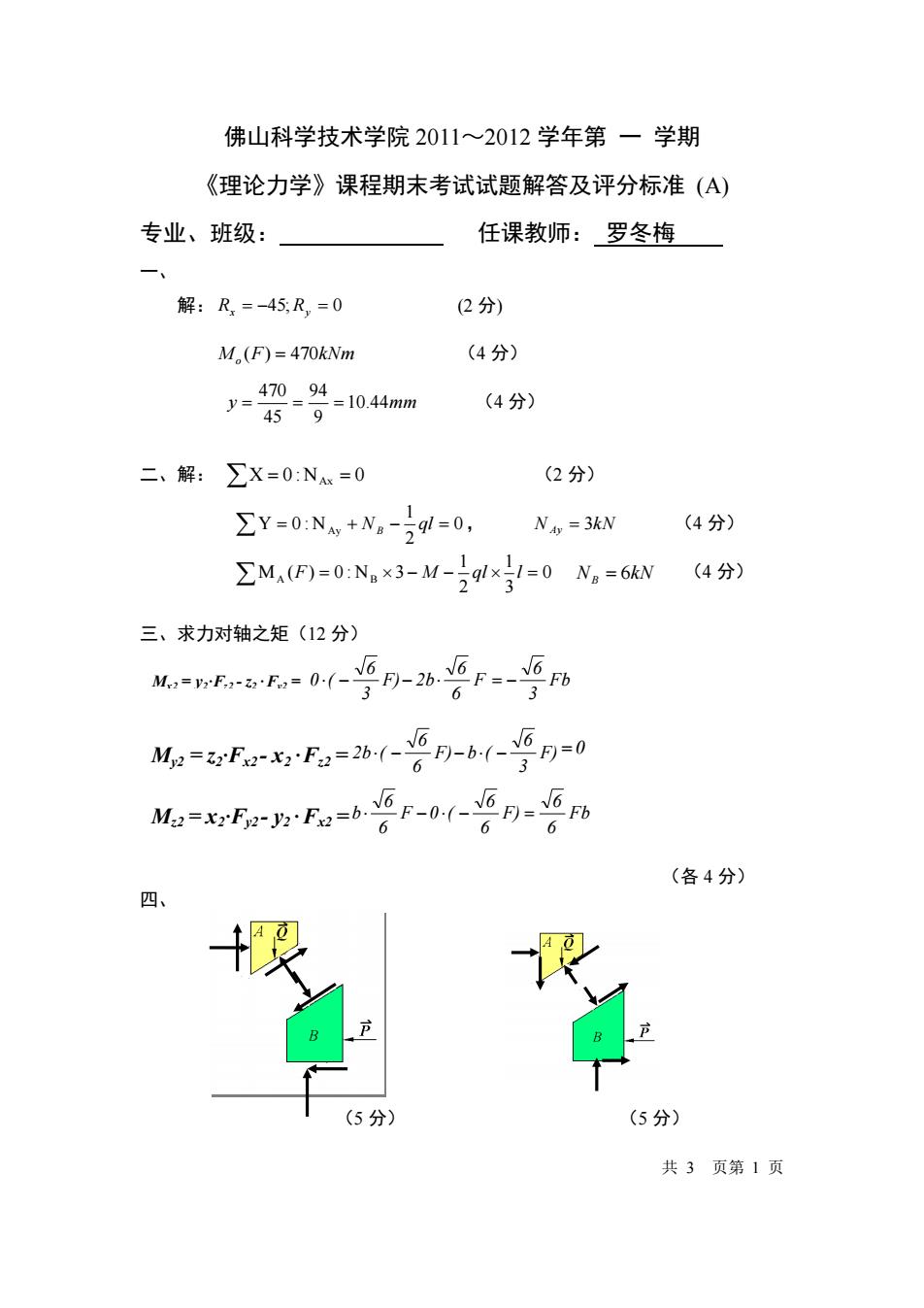
佛山科学技术学院2011~2012学年第一学期 《理论力学》课程期末考试试题解答及评分标准(A) 专业、班级： 任课教师：罗冬梅 一 解：R=-45,R,=0 (2分) M (F)=470kNm (4分) y=470、94 10.44mm (4分) 459 二、解： ∑X=0:NAx=0 (2分) ∑Y=0N+N,-9l=0, NAy =3kN (4分) ∑M,P=0:N。×3-M-391x=0N。=6MN (4分) 三、求力对轴之矩(12分) 6 M2-F2F2=2b--6 -61-当为=0 6 Ma FnyF-0F 6 6 6 (各4分) 四、 (5分) (5分) 共3页第1页

佛山科学技术学院 2011～2012 学年第 一 学期 《理论力学》课程期末考试试题解答及评分标准 (A) 专业、班级： 任课教师： 罗冬梅 一、 解： Rx = −45;Ry = 0 (2 分) Mo (F) = 470kNm （4 分） y 10.44mm 9 94 45 470 = = = （4 分） 二、解： X = 0 :NAx = 0 （2 分）  = + − = 0 2 1 Y 0 : NAy N ql B ， NAy = 3kN （4 分）  =  − −  = 0 3 1 2 1 MA (F) 0 : NB 3 M ql l NB = 6kN （4 分） 三、求力对轴之矩（12 分） （各 4 分） 四、 （5 分） （5 分） 共 3 页第 1 页 F 6 6 F) 2b 3 6 M 0 ( − −  x2 = y2·Fz2 - z2 ·Fy2 = Fb 3 6 = − F) 3 6 F) b ( 6 6 M 2b( − −  − y2 = z2·Fx2 - x2 ·Fz2 = =0 F) 6 6 F 0 ( 6 6 M b −  − z2 = x2·Fy2 - y2 ·Fx2 = Fb 6 6 =

五、x=Rsin2p=Rsin2oM y Rcos2p =Rcos2ot Vx 40 Rcos2ot (2分) v,=-40 Rsin2ot v=V,2+y,=4R@ (4分) c0s①，i1)=业=cos20 ax=-40Rsin2ot =-4afx 4=-4o2Rcos20m=-403y a=a;+a;=16Ro2 (4分) x2+y2=r2 六 Vr Ve (2分) Ve u ro (4分) sml20。=sin30°，sin120°=sin30° ao-55 (4分) 6 七、 P.=m Vc =2MoL P,mg vc:MoL (4分) P-VP+P:=1 -MoL (2分) 2 Lo1=J10+J2.0=3ML0(4分) 共3页第2页

五、x = Rsin2 = Rsin2t y = Rcos2 = Rcos2t （2分） （4 分） =-4 2 x 2 2 2 a = ax + ay = 16R （4分） 2 2 2 x + y = r 六、 （2 分） （4 分） ， （4 分） 七、 （4 分） P Px Py ML 2 2 2 17 = + = （2 分） （4 分） 共 3 页第 2 页 vx = 4 Rcos2t vy = -4 Rsin2t = + = 4R 2 y 2 x v v v cos( , ) = = cos 2 v v v i x   ax = -4 2Rsin2t ay = -4 2Rcos2t = - 4 2 y o o e sin120 sin30 v a v = 3 6 5 BO = 2 2 2 2 x 1 1 M L P m v P m v M L y C C   = = = =    2 LO1 = J1o + J 2o = 3ML va vr ve o r sin120 sin 30 u o  =

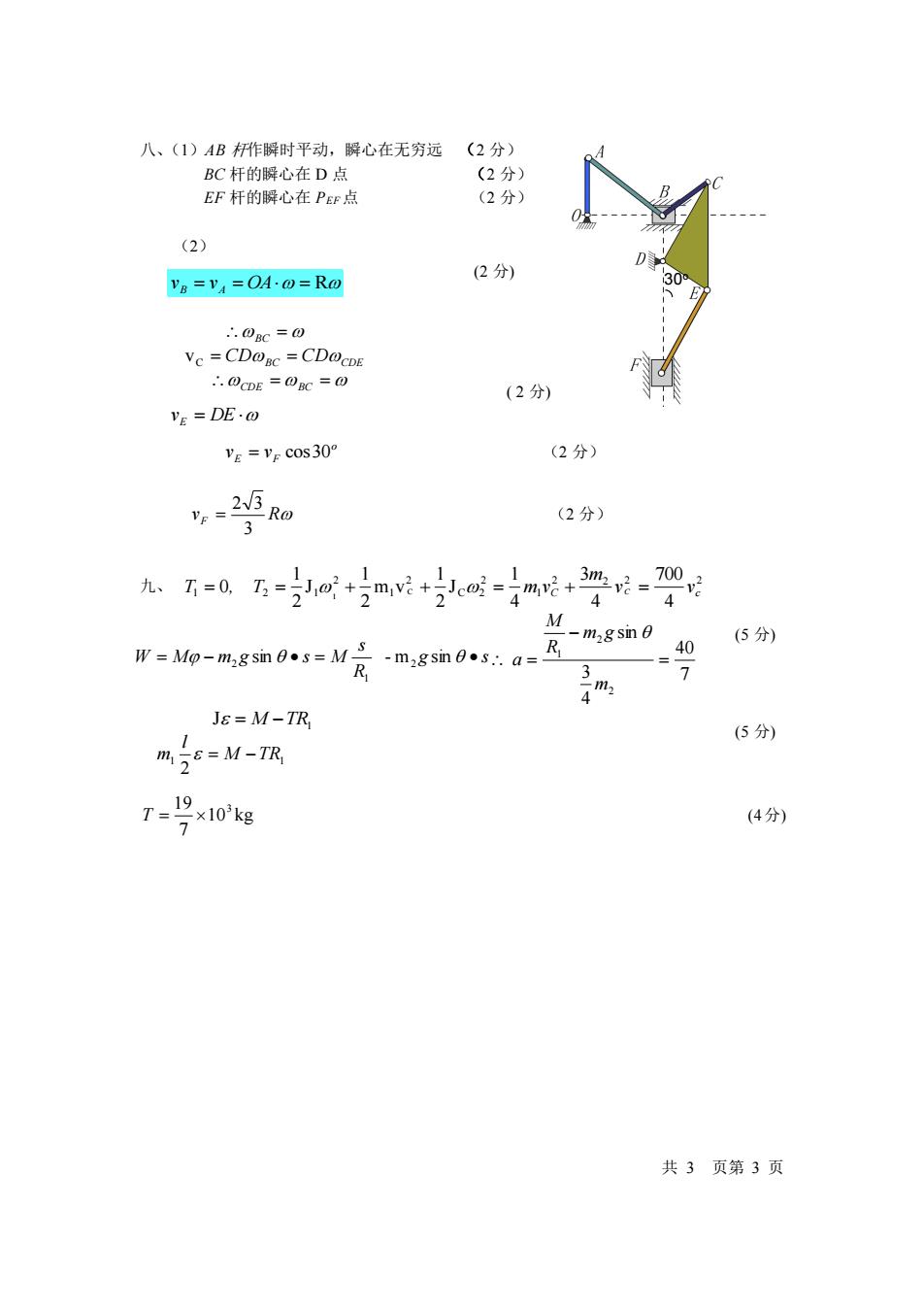
八、(1)AB杆作瞬时平动，瞬心在无穷远 (2分) BC杆的瞬心在D点 (2分) EF杆的瞬心在PEF点 (2分) (2) VB=V4=OA·0=Ro (2分) 30 ∴.0BC=0 Ve CDOBC =CD@CDE .OCDE =OBC =0 (2分) VE=DE·o VE=VE COS30 (2分) ,=-25R0 (2分) 3 1 4 4 M -m2gsin 0 (5分) W-Mo-magsin 0.s=M3-m2gsin 0.s..a= R 40 R 3 > Js=M-TR (5分) m78=M-TR T=x10 (4分) 共3页第3页

八、（1）AB 杆作瞬时平动，瞬心在无穷远 （2 分） BC 杆的瞬心在 D 点 （2 分） EF 杆的瞬心在 PEF 点 （2 分） （2） (2 分) ( 2 分) o E F v = v cos30 （2 分） vF R 3 2 3 = （2 分） 九、 (5 分) (5 分) 10 kg 7 19 3 T =  (4分) 共 3 页第 3 页 vB = vA = OA = R BC =  vC = CDBC = CDCDE vE = DE  2 2 2 2 1 2 C 2 2 1 2 1 2 1 4 700 4 3 4 1 J 2 1 m v 2 1 J 2 1 0 C 1 C c v v m T = , T =  + +  = m v + C = g s R s W = M − m g sin  • s = M - m sin  • 2 1 2 7 40 4 3 sin 2 2 1 = −  = m m g R M a  M TR l m1 1 2  = − 1 J = M −TR CDE =BC = 30o