
佛山科学技术学院2010~2011学年第一学期 《理论力学》课程期末考试试题解答及评分标准(A) 专业、班级: 任课教师:罗冬梅 一 (1)M-F.×2acos30°=0 (1分) F=M (1分) 3a F.-Fcos60°=0 Es③M (1分) 6a E+Fsin60-M/a=0 F-2a M (1分) M,-Mxa+Fsin60x2a-0 M,=0 (1分) a ow同=-w号-婴号-0 (3分) F=ga+ga =3ga 22 (3分) 二、求A点反力(12分) FL-Fx5L-0E=BF2分) 3 3 A300 F。-E。-9L=0F,=9L+5F2分) (2分) 3 F.=0(2分) M M,-FL-5=0M,=5+a分) FAx 分) 23 共4页第1页
佛山科学技术学院 2010~2011 学年第 一 学期 《理论力学》课程期末考试试题解答及评分标准 (A) 专业、班级: 任课教师: 罗冬梅 一. (1) − 2 cos30 = 0 o M FC a (1 分) a M FC 3 3 = (1 分) − cos60 = 0 o FAx FC a M FAX 6 3 = (1 分) F + F sin60 − M / a = 0 o Ay C a M FAy 2 = (1 分) − a + F sin 60 2a = 0 a M M o A C MA = 0 (1 分) (2) (3 分) (3 分) 二、求 A 点反力(12 分) 0 3 3 − = L FC L F 3 3F FC = (2 分) FAy − FC − qL = 0 3 3F FAy = qL + (2 分) (2 分) FAx = 0 (2 分) 0 2 2 − − = qL M A FC L 3 3 2 2 qL FL M A = + (2 分) (2 分) 共 4 页第 1 页 ( ) 2 6 5 3 2 2 2 qa a qa qa M A F = −qa − = 2 3 2 qa qa F = qa + = D F C 30O FC F q Ay FAx MA FB
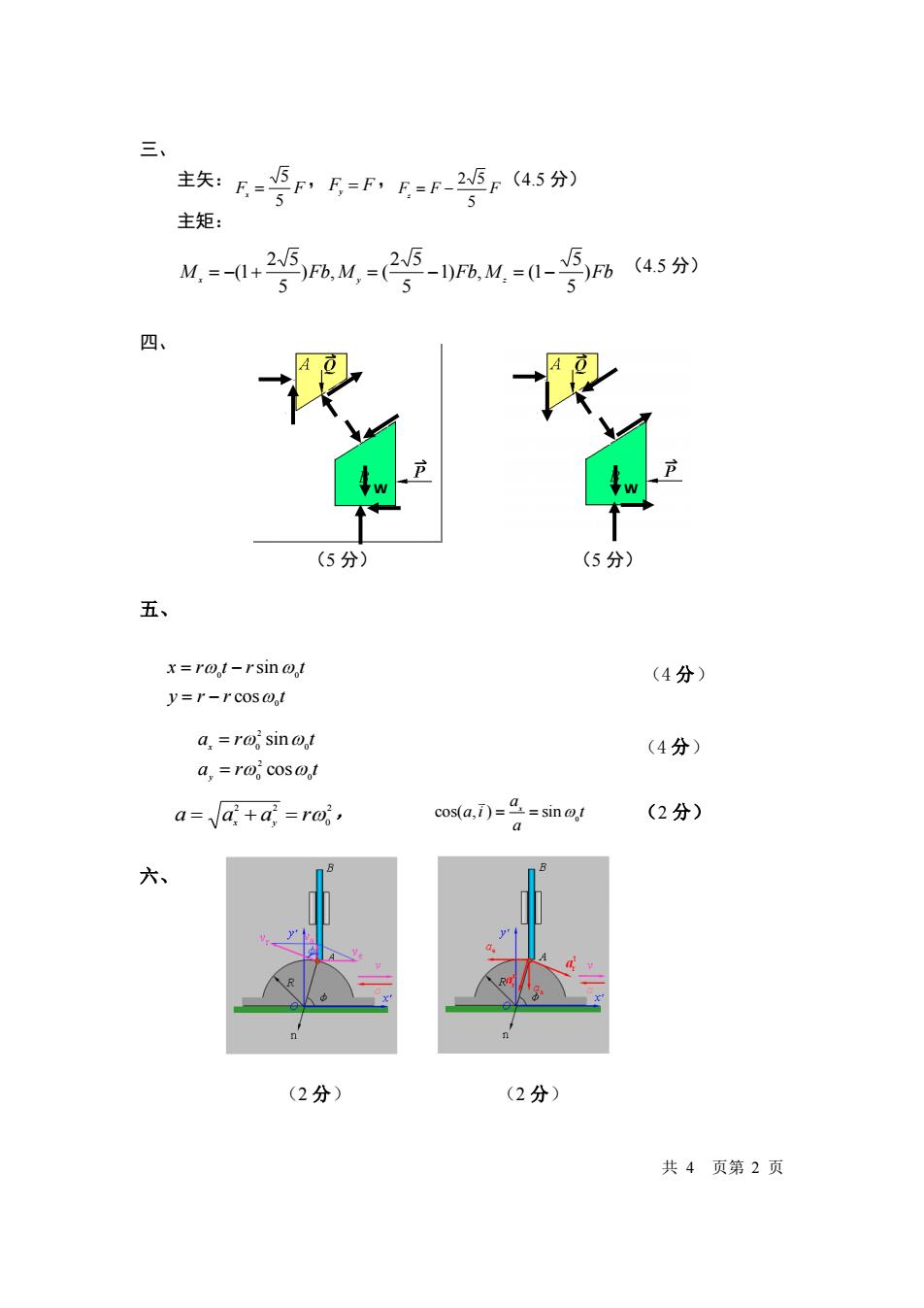
三 主矢:F=5F,F=F,E=F-25r45分) 主矩: M=-0+256以=(2g5-a=0-5645分) 5 四、 (5分) (5分) 五、 x=rot-rsin@t (4分) y=r-rcos@t a,=ro sinot (4分) a,=ra cos@t a=a;+a;=raj, cos(a,1)=4=sinot (2分) a 大、 (2分) (2分) 共4页第2页
三、 主矢: F x F 5 5 = ,F y = F ,F z F F 5 2 5 = − (4.5 分) 主矩: M x Fb M y Fb M z )Fb 5 5 1) , (1 5 2 5 ) , ( 5 2 5 = −(1+ = − = − (4.5 分) 四、 (5 分) (5 分) 五、 y r r t x r t r t 0 0 0 cos sin = − = − (4 分) a r t a r t y x 0 2 0 0 2 0 cos sin = = (4 分) 2 0 2 2 a = a x + a y = r , (2 分) 六、 (2 分) (2 分) 共 4 页第 2 页 t a a a i x 0 cos( , ) = = sin W W
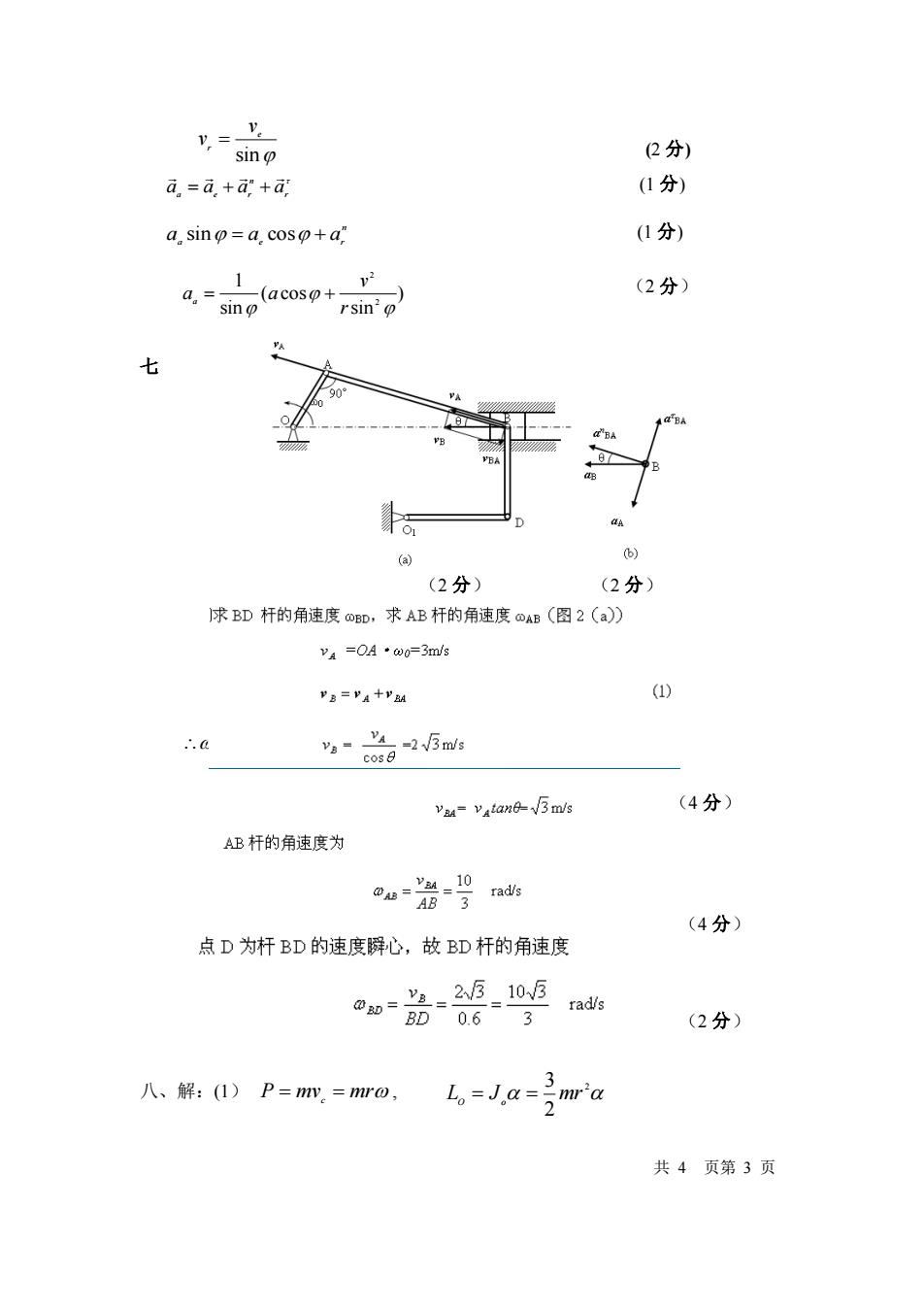
Y.-S n (2分) a。=a.++ (1分) a sino=a.coso+a" (1分) 1 v2 a.=si -(acoso+- (2分) rsin'o 七 90 PE ”EA (a) 6) (2分) (2分) 求BD杆的角速度oBD,求AB杆的角速度①AB(图2(a) vA=OA·o0=3mls "B="A十P的 (1) .∴.0 V8= vA-23 mis cos va=y4an√3ms (4分) AB杆的角速度为 QAB= '4-10 rad/s (4分) 点D为杆BD的速度瞬心,故BD杆的角速度 g=2W3105 0如三80062 rad/s (2分) 3 八、解:(1)P=m.=mr0, L。=J.a=号mra 共4页第3页
(2 分) r n a a a e a r a = + + (1 分) n a a = a e + a r sin cos (1 分) ) sin ( cos sin 1 2 2 r v a a a = + (2 分) 七 (2 分) (2 分) (4 分) (4 分) (2 分) 八、解:(1) P = mv c = mr , 2 2 3 L J mr O = o = 共 4 页第 3 页 sin e r v v = AB = 0

(2)F=-ma"=-mrwi,F=-ma:=-mra M。=-Ja=-mwa (各2分) 九、解: (1)动能定理 T=0 1 T-7J0i+ 1G g J0+ -(2G+G)w (2分) 2 W=Ghsina-Gh (2分) (2G+G)=(Gsina-G,)h 28 a=(Gsina-G) (2分) (2G+G) (2)∑M(F)=0: Ja+Gar-Gr+Tr-0 (2分) T=G,+(2G+G)sinaG (2分) 2(2G+G) ∑F(F)=0:X。-Tcosa=0X。=Tcosa (2分) >F(F)=0:Y+Ga-(G+G+Tsina)=0 (2分) Y=(G+G,+Tsina)-Ga (1)a=sina-Gig 答 2G+G1 (2)8e 3G+(2G +G)sin ag 2(2G+G1) (3)Nx= Gcosa3+(2+)sin@] 2(2G+G) G N,=2(20+G) (4G+6G+[5G +(2G +)sin a]sin a) 共4页第4页
(2) 2 F ma mrw n in = − c = − , F ma mr it = − c = − 2 2 3 M J mr iO = − o = − (各 2 分) 九、解: (1)动能定理 (2 分) (2 分) g G G G G a (2 ) ( sin ) 1 1 + − = (2 分) (2) M (F) = 0 : O 1 0 1 + ar − G r + Tr = g G J o (2 分) G G G G G G T 2(2 ) 3 (2 )sin 1 1 1 + + + = (2 分) F x (F) = 0: X o −T cos = 0 X0 = T cos (2 分) F y (F) = 0: ( 1 sin ) 0 1 + a − G + G +T = g G YO (2 分) a g G Y G G T 1 0 1 = ( + + sin) − 共 4 页第 4 页 W = Ghsin −G1h G G h g G G v ( sin ) 2 (2 ) 1 2 1 = − + 2 1 2 1 2 2 2 2 2 1 1 (2 ) 2 1 2 1 2 1 2 1 2 1 0 G G v g v g G v J g G T J T = A + o + o + c = + = O J0 G YO XO T G1 a g G1

共5页第5页
共 5 页第 5 页