
速度、加速度分量表示式
速度、加速度分量表示式

一 直角坐标系 空间基矢:i,方,k的方向不变 P (x,y,Z) 位置矢量下=xi+y方+zR 右手正交系:i×方=R X 2
一 直角坐标系 空间基矢: 位置矢量 i ˆ ,j ˆ ,k ˆ 的方向不变 r = xi ˆ + yj ˆ + zk ˆ 右手正交系: i ˆ j ˆ = k ˆ z y x O P(x,y,z) i ˆ j ˆ k ˆ r 2

对位置矢量求导:云 dr dx + dy dt dt dt dt i+方+之R =1 i+v方+yk 大 小:v立=√2+2+2 方向余弦: cma-s-。 SY= V 3
对位置矢量求导: 大 小: 方向余弦: v v v v v vx y z cos = , cos = , cos = r = xi ˆ + yj ˆ + zk ˆ v i v j v k xi yj zk k dt dz j dt dy i dt dx dt dr v x y z ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ = + + = + + = = + + 2 2 2 v |v | x y z = = + + 3

对速度求导: 三Vx +方+vk d a= 二 i+ dvz k dt dt dt = xi +苏+泳 4 中
对速度求导: xi yj zk = ˆ + ˆ + ˆ v = v x i ˆ + v y j ˆ + v z k ˆ k dt dv j dt dv i dt dv dt dv a = = x ˆ + y ˆ + z ˆ 4

二平面极坐标系 基矢: i p(r,0 向基矢,沿径向 横向基矢,垂直于 径向并指向0增加 的方向 极点 极轴 与直角坐标系不同,矢量沿质点所在的位置的 基矢“就地”进行正交分解。 5
二 平面极坐标系 与直角坐标系不同,矢量沿质点所在的位置的 基矢“就地”进行正交分解。 基矢: i ˆ 径向基矢,沿径向 j ˆ 极点 极轴 p(r,) o i ˆ j ˆ v 横向基矢,垂直于 径向并指向 增加 的方向 5

质点运动方程: y F dr dr di dt i +r dt dt de X 6
质点运动方程: r = ri ˆ dt di i r dt dr dt dr v ˆ = = ˆ + i ˆ j ˆ j ˆ di ˆ dj ˆ i ˆ o d d d Q P r x y 6
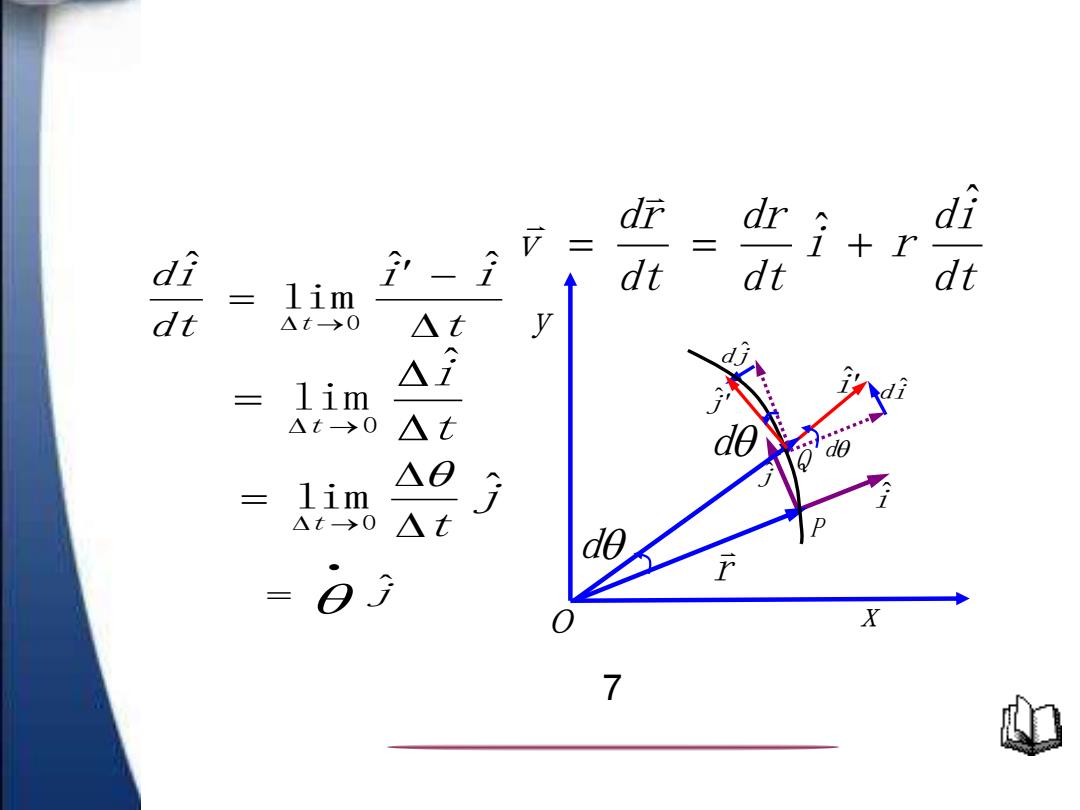
di r di - dt dt lim △t>0 △t y △f 二 lim △t>0 △t △0 lim △t>0 △t do X 7
dt di i r dt dr dt dr v ˆ = = ˆ + t i t = → ˆ lim 0 j t t lim ˆ 0 = → j ˆ • = t i i dt di t − = → ˆ ˆ lim ˆ 0 i ˆ j ˆ j ˆ di ˆ dj ˆ i ˆ o d d d Q P r x y 7
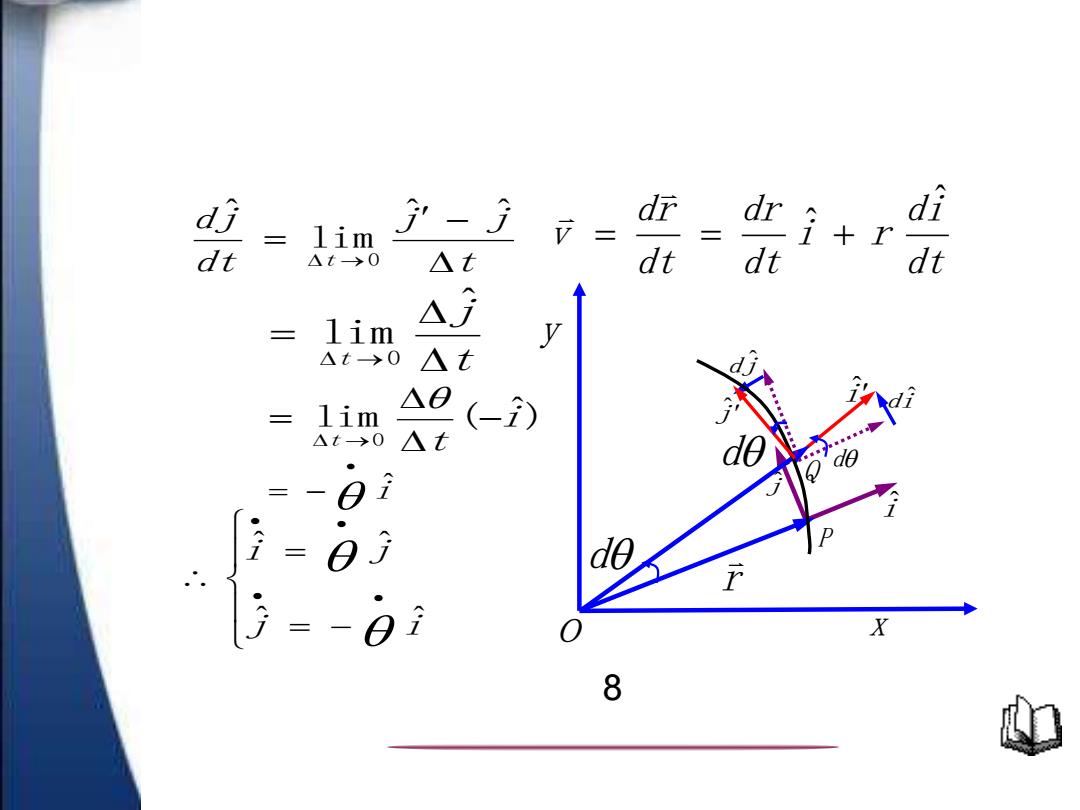
d} - dr i i lim 三 r dt △t>0 △t F 三 lim 4 y △t>0 △t △0 二 lim (-) △t>0 △t 0 三 X 8
dt di i r dt dr dt dr v ˆ = = ˆ + t j j dt dj t − = → ˆ ˆ lim ˆ 0 t j t = → ˆ lim 0 lim ( ˆ ) 0 i t t − = → i ˆ • = − = − = • • • • j i i j ˆ ˆ ˆ ˆ i ˆ j ˆ j ˆ di ˆ dj ˆ i ˆ o d d d Q P r x y 8
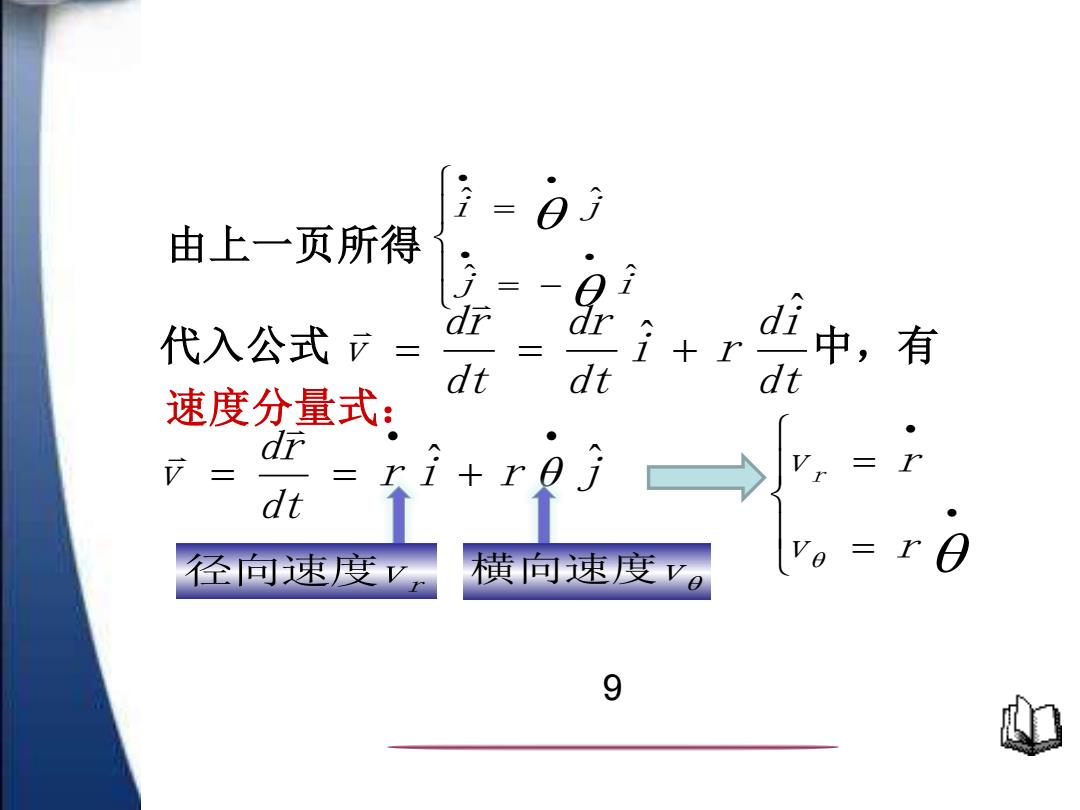
由上一页所得 dr 代入公式方= dt dt 十r dt 中,有 速度分量式: ● dr xi+r dt 径向速度V 横向速度v。 ,=r 9
dt di i r dt dr dt dr v ˆ = = ˆ + = − = • • • • j i i j ˆ ˆ ˆ ˆ 由上一页所得 代入公式 中,有 r i r j dt dr v ˆ ˆ • • = = + = = • • v r v r r 径向速度v r 横向速度v 速度分量式: 9

dr 市 = 二 +r9)=i+j ● 三 r 径向速度,是矢径量值变化产生的。 ve 三 r 横向速度,是矢径方向变化产生的。 10
r i r j dt dr v ˆ ˆ • • = = + 径向速度,是矢径量值 变 化产生的。 横向速度,是矢径方向变化产生的。 v i v j r ˆ ˆ = + • v r = r • v = r 10