
S16-6用求解器求极限荷载 S16-6用求解器求极限荷载 求解器可以计算一般平面结构的极限荷载并能静态或动画显示破坏机构的单向运动模 态。荷载可以是集中荷载或者均布荷载。由于极限荷载和各个杆件刚度无关,因此可以不输 入杆件刚度(当然输入也无妨)。因此,除了按常规输入结构体系外,还要输入各杆的极限弯 矩和对解答精度控制的误差限,求解器解出的解与精确解相比其误差不超过用户指定的误差 限。由于求解器采用精确求解,通常一个杆件取为一个单元即可。对于低版本的求解器,要 求集中荷载作用在结点上,这样杆件上如有集中荷载作用,就要再分单元以使集中荷载作用 点处成为一个结点。 杆件的极限弯矩的输入同杆件的刚度输入步骤一样,而且在同一个对话框中,这里不再 详述。为了输入误差限的值,依次选择菜单:“命令”、“其他参数”、“极限荷载”,从而打开 “误差限”对话框,然后输入数值即可。如果不输入误差限,求解器将使用缺省值0.05。以 下通过具体的例题作进一步的介绍。 例16-6-1试用求解器重新求解例15-6。单元及结点编码见图16-6-1。为比较方便,有关 数据采用单位值:I=lm,Mn=1kN·m。 TITLE,例16-6-1 结点,1,0,0 结点,2,0,1 结点,3,1,1 2 3 1.5M 结点,4,2,1 (2) (3) 结点,5,2,0 单元,1,2,1,1,1,1,1,1 M (1) 4 单元生成,3,1,1,1 结点支承,1,6,0,0,0,0 结点支承,5,6,0,0,0,0 结点荷载,2,1,1,0 结点荷载,3,1,1,-90 单元材料性质,1,4,0,0,0,1,-1 单元材料性质,2,3,0,0,0,1.5,-1 图16-6-1例16-6-1图 极限荷载参数,0.005 END 解输入的结构和命令文档如图16-6-1 所示。计算的极限荷载为3.5kN,与精确解 完全一样。求解器中显示的破坏机构模态在 图16-6-2中给出。 例16-6-2试用求解器求解图16-6-3中 所示的均布荷载作用下门式刚架的极限荷 载和破坏机构模态,有关数据为各杆长 图16-6-2例16-6-1的破坏机构运动模态 1=1m,Mm=10kNm
§16-6 用求解器求极限荷载 §16-6 用求解器求极限荷载 求解器可以计算一般平面结构的极限荷载并能静态或动画显示破坏机构的单向运动模 态。荷载可以是集中荷载或者均布荷载。由于极限荷载和各个杆件刚度无关,因此可以不输 入杆件刚度(当然输入也无妨)。因此,除了按常规输入结构体系外,还要输入各杆的极限弯 矩和对解答精度控制的误差限,求解器解出的解与精确解相比其误差不超过用户指定的误差 限。由于求解器采用精确求解,通常一个杆件取为一个单元即可。对于低版本的求解器,要 求集中荷载作用在结点上,这样杆件上如有集中荷载作用,就要再分单元以使集中荷载作用 点处成为一个结点。 杆件的极限弯矩的输入同杆件的刚度输入步骤一样,而且在同一个对话框中,这里不再 详述。为了输入误差限的值,依次选择菜单:“命令”、“其他参数”、“极限荷载”,从而打开 “误差限”对话框,然后输入数值即可。如果不输入误差限,求解器将使用缺省值 0.05。以 下通过具体的例题作进一步的介绍。 例 16-6-1 试用求解器重新求解例 15-6。单元及结点编码见图 16-6-1。为比较方便,有关 数据采用单位值:l = 1 m , Mu =1 kN ⋅m 。 TITLE,例 16-6-1 结点,1,0,0 结点,2,0,1 结点,3,1,1 结点,4,2,1 结点,5,2,0 单元,1,2,1,1,1,1,1,1 单元生成,3,1,1,1 结点支承,1,6,0,0,0,0 结点支承,5,6,0,0,0,0 结点荷载,2,1,1,0 结点荷载,3,1,1,-90 单元材料性质,1,4,0,0,0,1,-1 单元材料性质,2,3,0,0,0,1.5,-1 极限荷载参数,0.005 END 图 16-6-1 例 16-6-1 图 解 输入的结构和命令文档如图 16-6-1 所示。计算的极限荷载为 3.5 kN,与精确解 完全一样。求解器中显示的破坏机构模态在 图 16-6-2 中给出。 例 16-6-2 试用求解器求解图 16-6-3 中 所示的均布荷载作用下门式刚架的极限荷 载和破坏机构模态,有关数据为各杆长 l = 1 m , M u = 10 kN ⋅ m 。 图 16-6-2 例 16-6-1 的破坏机构运动模态 1
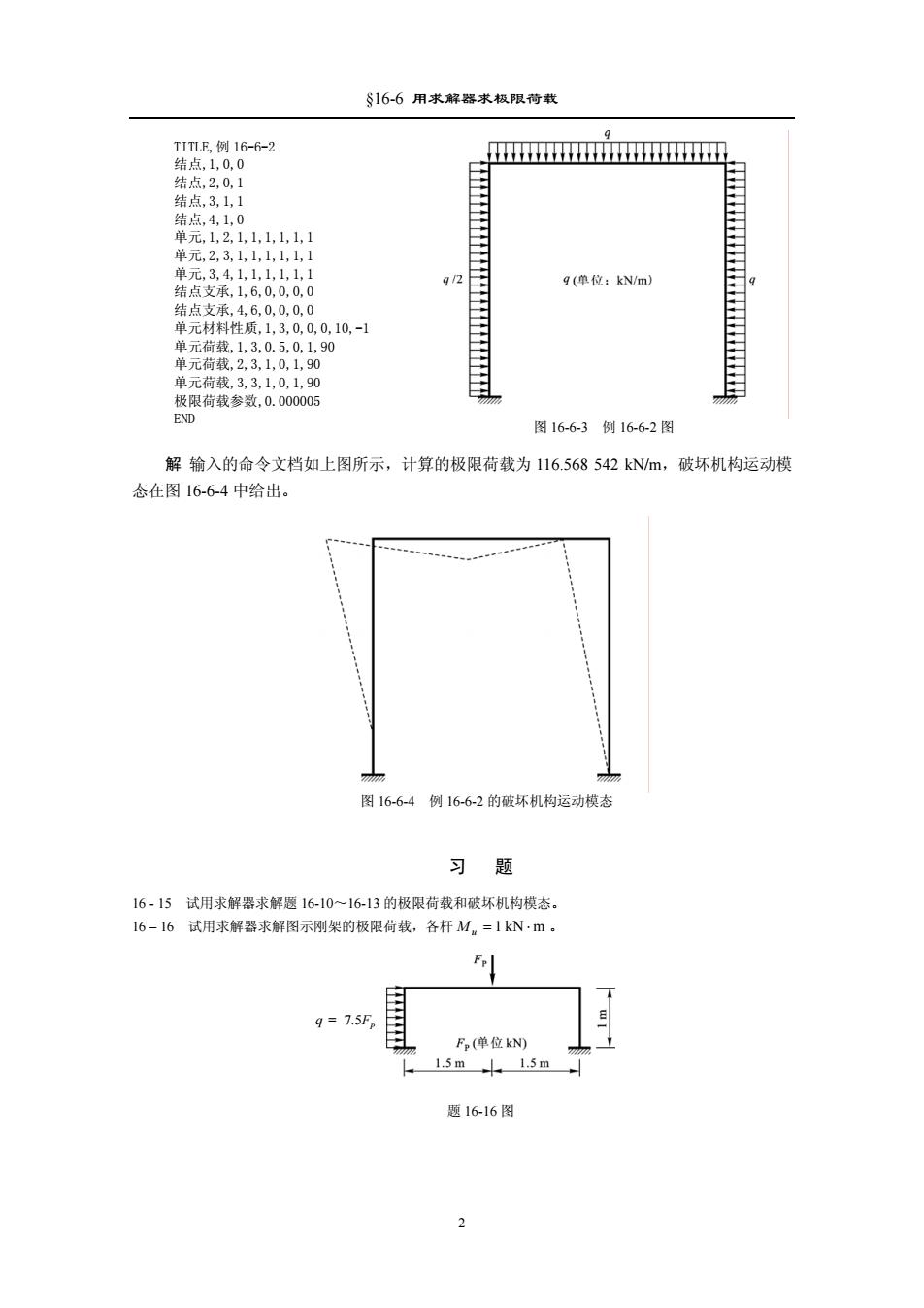
§16-6用求解器求极限荷载 TITLE,例16-6-2 结点,1,0,0 结点,2,0,1 结点,3,1,1 结点,4,1,0 单元,1,2,1,1,1,1,1,1 单元,2,3,1,1,1,1,1,1 单元,3,4,1,1,1,1,1,1 9/2 g(单位:kN/m) 结点支承,16,0,0,0,0 结点支承,4,6,0,0,0,0 单元材料性质,1,3,0,0,0,10,-1 单元荷载,1,3,0.5,0,1,90 单元荷载,2,3,1,0,1,90 单元荷载,3,3,1,0,1,90 极限荷载参数,0.000005 END 图16-6-3例16-6-2图 解输入的命令文档如上图所示,计算的极限荷载为116.568542kN/m,破坏机构运动模 态在图16-6-4中给出。 图16-6-4例16-6-2的破坏机构运动模态 习 题 16-15试用求解器求解题1610~16-13的极限荷载和破坏机构模态。 16-16试用求解器求解图示刚架的极限荷载,各杆M,=1kN.m。 q 7.5Fp F.(单位kN) 1.5m1.5m 题16-16图 2
§16-6 用求解器求极限荷载 TITLE,例 16-6-2 结点,1,0,0 结点,2,0,1 结点,3,1,1 结点,4,1,0 单元,1,2,1,1,1,1,1,1 单元,2,3,1,1,1,1,1,1 单元,3,4,1,1,1,1,1,1 结点支承,1,6,0,0,0,0 结点支承,4,6,0,0,0,0 单元材料性质,1,3,0,0,0,10,-1 单元荷载,1,3,0.5,0,1,90 单元荷载,2,3,1,0,1,90 单元荷载,3,3,1,0,1,90 极限荷载参数,0.000005 END 图 16-6-3 例 16-6-2 图 解 输入的命令文档如上图所示,计算的极限荷载为 116.568 542 kN/m,破坏机构运动模 态在图 16-6-4 中给出。 图 16-6-4 例 16-6-2 的破坏机构运动模态 习 题 16 - 15 试用求解器求解题 16-10~16-13 的极限荷载和破坏机构模态。 16 – 16 试用求解器求解图示刚架的极限荷载,各杆 M u = 1 kN ⋅ m 。 7.5 P q F = 题 16-16 图 2

§1-6结构力学求解器简介 §1-6结构力学求解器简介 把繁琐交给求解器,我们留下创造力! 本书所附的《结构力学求解器》(SM Solver for Windows,简称求解器)是一个方便好用 的计算机辅助分析计算软件(见所附光盘),其求解内容涵盖了本教材中所涉及的几乎所有问 题,包括:二维平面结构(体系)的几何组成、静定、超静定、位移、内力、影响线、自由 振动、弹性稳定、极限荷载等。对所有这些问题,求解器全部采用精确算法给出精确解答。 有关求解器的安装和使用简介可以参阅软件光盘上的相关文档和联机帮助,这里不作详 细讲解。本书中各个章节中大都会出现如何使用求解器的内容,供读者酌情选学或自学。由 于本书中主要将求解器当作工具来用,因此只在目录中列出相关内容的标题(以便为读者提 供一个循序渐进的向导),而具体内容则放到了光盘上,同时其内在的算法和原理将在其他教 材(参见袁驷编著,《程序结构力学》)中介绍。 在结构力学的学习中,求解器可以提供多种功用和帮助,有待于读者去熟悉和发现,这 里只列举几点。 1.结构计算求解的利器 求解器首先是一个计算求解的强有效的工具。犹如计算器的功能是做数值计算,求解器 的功能是做结构计算。任意平面结构输进求解器,鼠标一点,变形图和内力图即出。 2.体验大结构的受力性能 求解器并非专为课堂上小问题的求解而设计的。有了求解器,即便是结构力学的初学者, 也可以用求解器来方便地求解大结构的各类问题,以增强对大结构受力特性的直观感受和切 实体验。 3.求解传统方法难以求解的问题 本书中的传统方法并非都适用于精确求解大型实际结构,例如,几何构造分析的三角形 法则只适用于符合该法则的体系,超静定结构分析方法大都假定结构无轴向变形等等:而求 解器则全无这些限制。 4.演示和作图的工具 求解器可以用静态图形显示结构简图、变形图、内力图,还可以用动画显示机构模态、 振型等动态图形。利用复制到剪贴板的功能,可以将结构简图、变形图、内力图以点阵图或 矢量图的形式粘贴到MS Word或MS PowerPoint中,并可以方便地进行再编辑。 5.让求解器当教师答疑 几何构造分析选不出刚片吗?静定桁架的截面法剖不出截面单杆?静定组合结构分析不 知道从哪里开始下手?求解器的智能求解功能可以将求解步骤一步步地演示出来。 6.定性分析的数值试验平台 将桁架的结点都设为刚结点,看看弯曲应力是不是次应力?对于多层刚架,强梁弱柱和 强柱弱梁的受力特点有什么不同?梁的剪切变形是否小到可以忽略?这些都可以用求解器来 做具体的试验和验证。 1
§1-6 结构力学求解器简介 §1-6 结构力学求解器简介 把繁琐交给求解器,我们留下创造力! 本书所附的《结构力学求解器》(SM Solver for Windows,简称求解器)是一个方便好用 的计算机辅助分析计算软件(见所附光盘),其求解内容涵盖了本教材中所涉及的几乎所有问 题,包括:二维平面结构(体系)的几何组成、静定、超静定、位移、内力、影响线、自由 振动、弹性稳定、极限荷载等。对所有这些问题,求解器全部采用精确算法给出精确解答。 有关求解器的安装和使用简介可以参阅软件光盘上的相关文档和联机帮助,这里不作详 细讲解。本书中各个章节中大都会出现如何使用求解器的内容,供读者酌情选学或自学。由 于本书中主要将求解器当作工具来用,因此只在目录中列出相关内容的标题(以便为读者提 供一个循序渐进的向导),而具体内容则放到了光盘上,同时其内在的算法和原理将在其他教 材(参见袁驷编著,《程序结构力学》)中介绍。 在结构力学的学习中,求解器可以提供多种功用和帮助,有待于读者去熟悉和发现,这 里只列举几点。 1. 结构计算求解的利器 求解器首先是一个计算求解的强有效的工具。犹如计算器的功能是做数值计算,求解器 的功能是做结构计算。任意平面结构输进求解器,鼠标一点,变形图和内力图即出。 2. 体验大结构的受力性能 求解器并非专为课堂上小问题的求解而设计的。有了求解器,即便是结构力学的初学者, 也可以用求解器来方便地求解大结构的各类问题,以增强对大结构受力特性的直观感受和切 实体验。 3. 求解传统方法难以求解的问题 本书中的传统方法并非都适用于精确求解大型实际结构,例如,几何构造分析的三角形 法则只适用于符合该法则的体系,超静定结构分析方法大都假定结构无轴向变形等等;而求 解器则全无这些限制。 4. 演示和作图的工具 求解器可以用静态图形显示结构简图、变形图、内力图,还可以用动画显示机构模态、 振型等动态图形。利用复制到剪贴板的功能,可以将结构简图、变形图、内力图以点阵图或 矢量图的形式粘贴到 MS Word 或 MS PowerPoint 中,并可以方便地进行再编辑。 5. 让求解器当教师答疑 几何构造分析选不出刚片吗?静定桁架的截面法剖不出截面单杆?静定组合结构分析不 知道从哪里开始下手?求解器的智能求解功能可以将求解步骤一步步地演示出来。 6. 定性分析的数值试验平台 将桁架的结点都设为刚结点,看看弯曲应力是不是次应力?对于多层刚架,强梁弱柱和 强柱弱梁的受力特点有什么不同?梁的剪切变形是否小到可以忽略?这些都可以用求解器来 做具体的试验和验证。 1
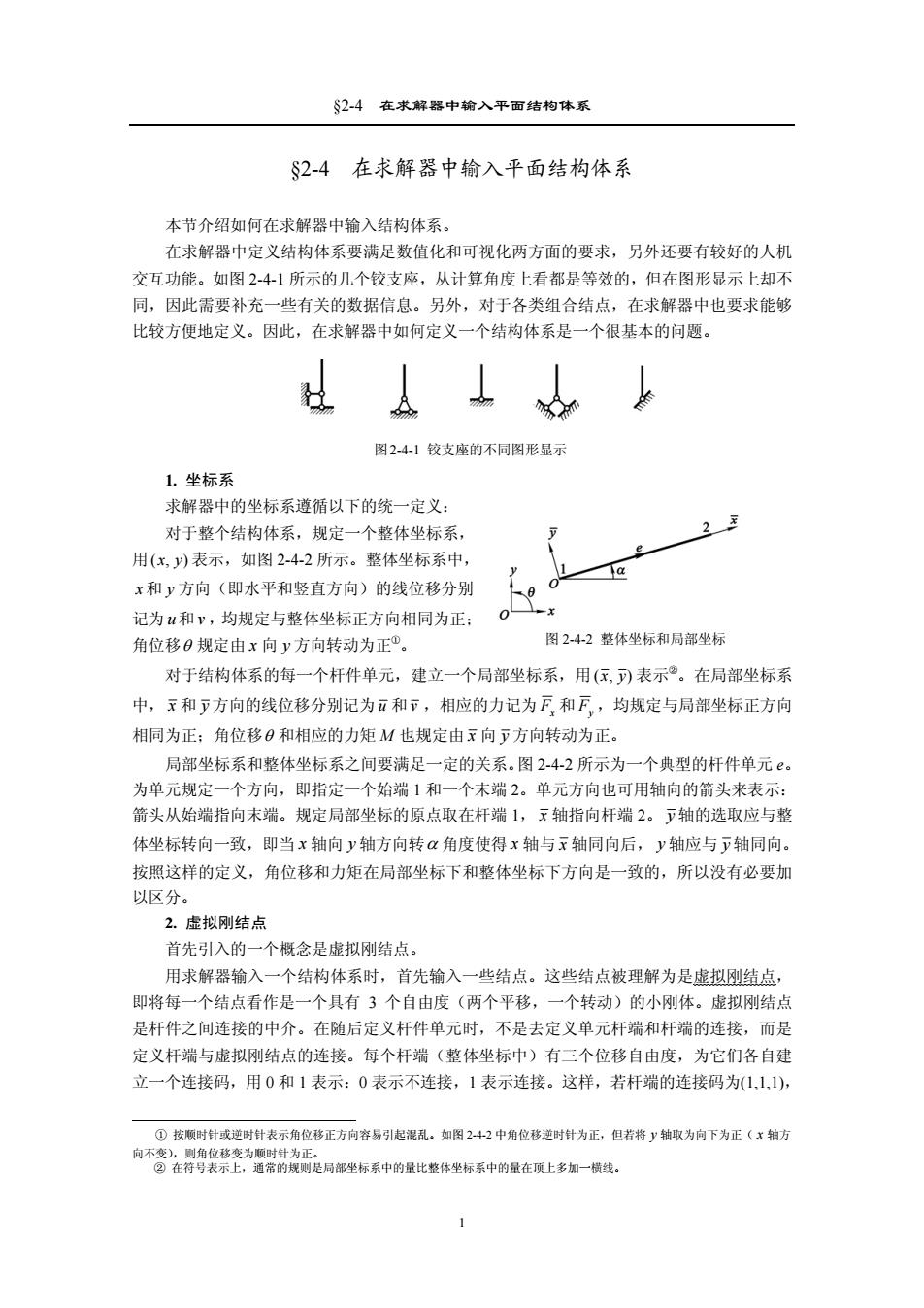
S2-4在求解器中输入平面结构体系 2-4在求解器中输入平面结构体系 本节介绍如何在求解器中输入结构体系。 在求解器中定义结构体系要满足数值化和可视化两方面的要求,另外还要有较好的人机 交互功能。如图2-4-1所示的几个铰支座,从计算角度上看都是等效的,但在图形显示上却不 同,因此需要补充一些有关的数据信息。另外,对于各类组合结点,在求解器中也要求能够 比较方便地定义。因此,在求解器中如何定义一个结构体系是一个很基本的问题。 图2-41较支座的不同图形显示 1.坐标系 求解器中的坐标系遵循以下的统一定义: 对于整个结构体系,规定一个整体坐标系, 用(x,y)表示,如图2-4-2所示。整体坐标系中, x和y方向(即水平和竖直方向)的线位移分别 记为u和v,均规定与整体坐标正方向相同为正: 角位移0规定由x向y方向转动为正①。 图2-4-2整体坐标和局部坐标 对于结构体系的每一个杆件单元,建立一个局部坐标系,用(:,可)表示②。在局部坐标系 中,下和少方向的线位移分别记为和下,相应的力记为F和F,均规定与局部坐标正方向 相同为正:角位移日和相应的力矩M也规定由x向下方向转动为正。 局部坐标系和整体坐标系之间要满足一定的关系。图2-4-2所示为一个典型的杆件单元。 为单元规定一个方向,即指定一个始端1和一个末端2。单元方向也可用轴向的箭头来表示: 箭头从始端指向末端。规定局部坐标的原点取在杆端1,下轴指向杆端2。下轴的选取应与整 体坐标转向一致,即当x轴向y轴方向转心角度使得x轴与x轴同向后,y轴应与y轴同向。 按照这样的定义,角位移和力矩在局部坐标下和整体坐标下方向是一致的,所以没有必要加 以区分。 2.虚拟刚结点 首先引入的一个概念是虚拟刚结点。 用求解器输入一个结构体系时,首先输入一些结点。这些结点被理解为是虚拟刚结点, 即将每一个结点看作是一个具有3个自由度(两个平移,一个转动)的小刚体。虚拟刚结点 是杆件之间连接的中介。在随后定义杆件单元时,不是去定义单元杆端和杆端的连接,而是 定义杆端与虚拟刚结点的连接。每个杆端(整体坐标中)有三个位移自由度,为它们各自建 立一个连接码,用0和1表示:0表示不连接,1表示连接。这样,若杆端的连接码为(1,1,1), ①按顺时针或逆时针表示角位移正方向容易引起混乱。如图242中角位移逆时针为正,但若将y轴取为向下为正(x轴方 向不变),则角位移变为顺时针为正。 ②在符号表示上,通常的规则是局部坐标系中的量比整体坐标系中的量在顶上多加一横线
§2-4 在求解器中输入平面结构体系 §2-4 在求解器中输入平面结构体系 本节介绍如何在求解器中输入结构体系。 在求解器中定义结构体系要满足数值化和可视化两方面的要求,另外还要有较好的人机 交互功能。如图 2-4-1 所示的几个铰支座,从计算角度上看都是等效的,但在图形显示上却不 同,因此需要补充一些有关的数据信息。另外,对于各类组合结点,在求解器中也要求能够 比较方便地定义。因此,在求解器中如何定义一个结构体系是一个很基本的问题。 图2-4-1 铰支座的不同图形显示 1. 坐标系 求解器中的坐标系遵循以下的统一定义: 对于整个结构体系,规定一个整体坐标系, 用(x, y) 表示,如图 2-4-2 所示。整体坐标系中, x 和 方向(即水平和竖直方向)的线位移分别 记为u和 ,均规定与整体坐标正方向相同为正; 角位移 y v θ 规定由 x 向 y 方向转动为正①。 图 2-4-2 整体坐标和局部坐标 对于结构体系的每一个杆件单元,建立一个局部坐标系,用(x, y) 表示②。在局部坐标系 中, x 和 y 方向的线位移分别记为u 和 v ,相应的力记为 Fx 和 Fy ,均规定与局部坐标正方向 相同为正;角位移θ 和相应的力矩 M 也规定由 x 向 y 方向转动为正。 局部坐标系和整体坐标系之间要满足一定的关系。图 2-4-2 所示为一个典型的杆件单元 e。 为单元规定一个方向,即指定一个始端 1 和一个末端 2。单元方向也可用轴向的箭头来表示: 箭头从始端指向末端。规定局部坐标的原点取在杆端 1, x 轴指向杆端 2。 y 轴的选取应与整 体坐标转向一致,即当 x 轴向 y 轴方向转α 角度使得 x 轴与 x 轴同向后, y 轴应与 y 轴同向。 按照这样的定义,角位移和力矩在局部坐标下和整体坐标下方向是一致的,所以没有必要加 以区分。 2. 虚拟刚结点 首先引入的一个概念是虚拟刚结点。 用求解器输入一个结构体系时,首先输入一些结点。这些结点被理解为是虚拟刚结点, 即将每一个结点看作是一个具有 3 个自由度(两个平移,一个转动)的小刚体。虚拟刚结点 是杆件之间连接的中介。在随后定义杆件单元时,不是去定义单元杆端和杆端的连接,而是 定义杆端与虚拟刚结点的连接。每个杆端(整体坐标中)有三个位移自由度,为它们各自建 立一个连接码,用 0 和 1 表示:0 表示不连接,1 表示连接。这样,若杆端的连接码为(1,1,1), ① 按顺时针或逆时针表示角位移正方向容易引起混乱。如图 2-4-2 中角位移逆时针为正,但若将 y 轴取为向下为正( x 轴方 向不变),则角位移变为顺时针为正。 ② 在符号表示上,通常的规则是局部坐标系中的量比整体坐标系中的量在顶上多加一横线。 1

$24在求解器中输入平面结构体系 则该杆端与虚拟刚结点为刚结:(1,1,0)为铰结:(1,0,0)为水平链杆连接:(0,1,1)则为定向(水 平滑动)连接,等等。 下面结合图2-4-3~2-4-4中的例子来讨论。 (1,1,1)(1,1,1) (1,1,1)(1,1,1) (1,1,1) (1,1,1) → (a) (6) 图2-4-3刚结点的连接 4.1D.10 (1,1,1)(1,1,0) (1,1,1) → (1,1,1) (a) (b) 图24-4组合结点的连接 图2-4-3是刚结点的连接示例,其中图2-4-3a中定义了一个虚拟刚结点和杆端的连接码: 各个杆端与虚拟刚结点连接后成为图2-4-3b的形式,去除虚拟刚结点后的效果为图2-4-3c所 示的刚结点:求解器中显示的是最后的图2-4-3C。图2-44是组合结点的连接示例,同理,无 需重复。铰结点是最常见的结点之一,其连接示例在图2-4-5中给出。这里,共有四种连接方 式,都等效于图2-4-5e中的饺结点,通常采用图2-4-5a所示方式即可。值得一提的是,如果 将三个杆件固定住,图2-4-5b~d中的虚拟刚结点也随之被固定不动,而图2-4-5a中的虚拟刚 结点仍然存在一个转动自由度,可以绕结点自由转动。这是一种结点转动机构,在求解器中 会自动将其排除不计①。结点机构实际上也潜存于经典的结构力学之中,如将一个集中力矩加 在铰结点上,便可以理解为加在了结点机构上(犹如加在可自由转动的销钉上),是无意义的。 (a) (b) (1,1,0) (1,1,0) (1,1,1) (1,1,0) 00 (1,1,0) (1,1,0) (c) (1,1,0) (1,1,1) (1,1,0) (1,1,0) 0 (1,1,0) (1,1,1) e 图2-4-5铰结点的连接 综上所述,求解器中单元对话框中的“连接方式”是指各杆端与虚拟刚结点的连接方式, 而不是杆件之间的连接方式。这样,各杆件通过虚拟刚结点这一中介再和其他杆件间接地连 ①极限分析中的结点机构将被视为破杯机构的一种。 2
§2-4 在求解器中输入平面结构体系 则该杆端与虚拟刚结点为刚结;(1,1,0)为铰结;(1,0,0)为水平链杆连接;(0,1,1)则为定向(水 平滑动)连接,等等。 下面结合图 2-4-3~2-4-4 中的例子来讨论。 图 2-4-3 刚结点的连接 图 2-4-4 组合结点的连接 图 2-4-3 是刚结点的连接示例,其中图 2-4-3a 中定义了一个虚拟刚结点和杆端的连接码; 各个杆端与虚拟刚结点连接后成为图 2-4-3b 的形式,去除虚拟刚结点后的效果为图 2-4-3c 所 示的刚结点;求解器中显示的是最后的图 2-4-3c。图 2-4-4 是组合结点的连接示例,同理,无 需重复。铰结点是最常见的结点之一,其连接示例在图 2-4-5 中给出。这里,共有四种连接方 式,都等效于图 2-4-5e 中的铰结点,通常采用图 2-4-5a 所示方式即可。值得一提的是,如果 将三个杆件固定住,图 2-4-5b~d 中的虚拟刚结点也随之被固定不动,而图 2-4-5a 中的虚拟刚 结点仍然存在一个转动自由度,可以绕结点自由转动。这是一种结点转动机构,在求解器中 会自动将其排除不计①。结点机构实际上也潜存于经典的结构力学之中,如将一个集中力矩加 在铰结点上,便可以理解为加在了结点机构上(犹如加在可自由转动的销钉上),是无意义的。 图 2-4-5 铰结点的连接 综上所述,求解器中单元对话框中的“连接方式”是指各杆端与虚拟刚结点的连接方式, 而不是杆件之间的连接方式。这样,各杆件通过虚拟刚结点这一中介再和其他杆件间接地连 ① 极限分析中的结点机构将被视为破坏机构的一种。 2

S2-4在求解器中输入平面结构体系 接。这种处理的好处是可以避免结点的重复编码(如本书中矩阵位移法中所介绍的),同时可 以方便地构造各种复杂的组合结点。 另外,在定义位移约束时,结点处的支座约束也是首先加在虚拟刚结点上,再通过虚拟 刚结点施加给其他相关的杆端。 有了虚拟刚结点的概念,其他的具体做法都己比较显而易见,通过具体例题便很容易搞 懂。因此,以下基本上以例题来代替叙述。疑问之处,可以参见求解器的联机帮助。 3.输入结构体系 欲输入一个结构体系,首先在“编辑器”中打开一个新文件,然后输入命令。在求解器 中输入命令有两种方法: (1)利用“命令”菜单中的子菜单,打开相应的对话框,在对话框中根据提示和选项输入 命令。 (2)在文件中直接键入命令行。 第(1)种方法可以免除用户记忆命令格式,且可以利用对话框中的预览功能随时修正输入 的命令。如果用户对命令格式较熟悉,则直接键入命令更为快捷。本盘在附录中给出了所有 命令的语法规则和格式,需要时可以查阅。 修改命令也有两种方法: 1)将光标置于要修改的命令行,单击工具栏上的“修改”按钮(或在“命令”菜单下选 “修改”子菜单),则求解器将自动打开相应的命令对话框,对话框中的各选项再现了该条命 令中的各个参数,用户可以查看或修改。 2)在文件中直接修改命令行。 求解器中的每一条命令都由一关键词作先导,自版本V1.5开始,在保留原来的英文关键 词的同时,允许使用相应的中文关键词,在功能上它们是等效的。英文关键词键入方便,中 文关键词易读易辨。求解器中默认的选择是中文关键词,如果希望用英文关键词的话,可在 “查看”菜单下去除“中文关键词”的选项。本盘的附录中给出了所有命令的中英文关键词 的对照,需要时可以查询。本盘中大都采用中文关键词。 以下例题中,首先给出完成的命令数据文档,同时给出输入后的结构体系的图例,然后 对个别命令行的输入作简要说明。 例2-4-1在求解器中输入图2-4-6a所示的结构体系。 7 (5) 5 (4) (6 (2) 1) (3 1 m 1.5m (a)平面结构 (b)输入后显示的结构 图2-4-6结构的数值化定义
§2-4 在求解器中输入平面结构体系 接。这种处理的好处是可以避免结点的重复编码(如本书中矩阵位移法中所介绍的),同时可 以方便地构造各种复杂的组合结点。 另外,在定义位移约束时,结点处的支座约束也是首先加在虚拟刚结点上,再通过虚拟 刚结点施加给其他相关的杆端。 有了虚拟刚结点的概念,其他的具体做法都已比较显而易见,通过具体例题便很容易搞 懂。因此,以下基本上以例题来代替叙述。疑问之处,可以参见求解器的联机帮助。 3. 输入结构体系 欲输入一个结构体系,首先在“编辑器”中打开一个新文件,然后输入命令。在求解器 中输入命令有两种方法: (1)利用“命令”菜单中的子菜单,打开相应的对话框,在对话框中根据提示和选项输入 命令。 (2)在文件中直接键入命令行。 第(1)种方法可以免除用户记忆命令格式,且可以利用对话框中的预览功能随时修正输入 的命令。如果用户对命令格式较熟悉,则直接键入命令更为快捷。本盘在附录中给出了所有 命令的语法规则和格式,需要时可以查阅。 修改命令也有两种方法: 1) 将光标置于要修改的命令行,单击工具栏上的“修改”按钮(或在“命令”菜单下选 “修改”子菜单),则求解器将自动打开相应的命令对话框,对话框中的各选项再现了该条命 令中的各个参数,用户可以查看或修改。 2)在文件中直接修改命令行。 求解器中的每一条命令都由一关键词作先导,自版本 v1.5 开始,在保留原来的英文关键 词的同时,允许使用相应的中文关键词,在功能上它们是等效的。英文关键词键入方便,中 文关键词易读易辨。求解器中默认的选择是中文关键词,如果希望用英文关键词的话,可在 “查看”菜单下去除“中文关键词”的选项。本盘的附录中给出了所有命令的中英文关键词 的对照,需要时可以查询。本盘中大都采用中文关键词。 以下例题中,首先给出完成的命令数据文档,同时给出输入后的结构体系的图例,然后 对个别命令行的输入作简要说明。 例 2-4-1 在求解器中输入图 2-4-6a 所示的结构体系。 图 2-4-6 结构的数值化定义 3

S2-4在求解器中输入平面结构体系 解输入后的结构如图24-6b所示,命令数据文档如下,其中左边和右边分别为中、英文 关键词命令数据文档。 结点,1,0,0 N,1,0,0 结点,2,0,1 N,2,0,1 结点,3,1,1 N,3,1,1 结点,4,1,0 N,4,1,0 结点,5,1,2 N,5,1,2 结点,6,2.5,0 N,6,2.5,0 结点,7,2.5,2.5 N,7,2.5,2.5 单元,1,2,1,1,0,1,1,1 E,1,2,1,1,0,1,1,1 单元,2,3,1,1,1,1,1,0 E,2,3,1,1,1,1,1,0 单元,4,3,1,1,0,1,1,1 E,4,3,1,1,0,1,1,1 单元,3,5,1,1,1,1,1,1 E,3,5,1,1,1,1,1,1 单元,5,7,1,1,1,1,1,0 E,5,7,1,1,1,1,1,0 单元,6,7,1,1,1,1,1,0 E,6,7,1,1,1,1,1,0 结点支承,1,4,0,0,0 NSUPT,1,4,0,0,0 结点支承,4,4,0,0,0 NSUPT,4,4,0,0,0 结点支承,6,6,0,0,0,0 NSUPT,6,6,0,0,0,0 END END 以上命令数据中主要有三种命令:结点定义、单元定义、结点支承定义。下面分别讨论 如何用对话框输入这些命令。 (1)结点定义 以第一行命令“结点,1,0,0”为例:其中“结点”或“N”为关键词:后面的1为结点码: 0,0为整体坐标值。用对话框输入该命令的步骤如下: )在“命令”菜单下选择“结点”子菜单,打开结点对话框:此时,默认的命令选择是 结点定义。 2)在“结点码”下拉框中输入(或从下拉选项中选)1。 3)在“坐标x”和“y”下拉框中分别输入0,0。 4)单击“预览”按钮,可以在观览器中看到结点1的显示。 5)若不满意,可以修改以上输入。 6)单击“应用”按钮,将命令写到文档上。 7)可以继续输入下一个命令。 8)完成输入后,单击“关闭”按钮,关闭结点对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会同步显示出该结点。其余结点的 输入类似。 (2)单元定义 在结点定义命令后面的是单元定义命令。此时,要用到虚拟刚结点的概念。第一行单元 定义命令为:“单元,1,2,1,1,0,1,1,1”:其中关键词“单元”或“E”后面的1,2为单元两端 的结点码:随后的6个数据是两端点与虚拟刚结点1,2的连接码。用对话框输入该命令步骤 如下: 1)在“命令”菜单下选择“单元”子菜单,打开单元对话框:此时,默认的命令选择 是单元定义。 2)单元编码按照输入顺序自动排列,因此没有单元码输入选项。 3)在“杆端1”的“连接结点”处输入1,“连接方式”选“铰结
§2-4 在求解器中输入平面结构体系 解 输入后的结构如图 2-4-6b 所示,命令数据文档如下,其中左边和右边分别为中、英文 关键词命令数据文档。 结点,1,0,0 结点,2,0,1 结点,3,1,1 结点,4,1,0 结点,5,1,2 结点,6,2.5,0 结点,7,2.5,2.5 单元,1,2,1,1,0,1,1,1 单元,2,3,1,1,1,1,1,0 单元,4,3,1,1,0,1,1,1 单元,3,5,1,1,1,1,1,1 单元,5,7,1,1,1,1,1,0 单元,6,7,1,1,1,1,1,0 结点支承,1,4,0,0,0 结点支承,4,4,0,0,0 结点支承,6,6,0,0,0,0 END N,1,0,0 N,2,0,1 N,3,1,1 N,4,1,0 N,5,1,2 N,6,2.5,0 N,7,2.5,2.5 E,1,2,1,1,0,1,1,1 E,2,3,1,1,1,1,1,0 E,4,3,1,1,0,1,1,1 E,3,5,1,1,1,1,1,1 E,5,7,1,1,1,1,1,0 E,6,7,1,1,1,1,1,0 NSUPT,1,4,0,0,0 NSUPT,4,4,0,0,0 NSUPT,6,6,0,0,0,0 END 以上命令数据中主要有三种命令:结点定义、单元定义、结点支承定义。下面分别讨论 如何用对话框输入这些命令。 (1)结点定义 以第一行命令“结点,1,0,0”为例;其中“结点”或“N”为关键词;后面的 1 为结点码; 0,0 为整体坐标值。用对话框输入该命令的步骤如下: 1)在“命令”菜单下选择“结点”子菜单,打开结点对话框;此时,默认的命令选择是 结点定义。 2)在“结点码”下拉框中输入(或从下拉选项中选)1。 3)在“坐标 x”和“y”下拉框中分别输入 0,0。 4)单击“预览”按钮,可以在观览器中看到结点 1 的显示。 5)若不满意,可以修改以上输入。 6)单击“应用”按钮,将命令写到文档上。 7)可以继续输入下一个命令。 8)完成输入后,单击“关闭”按钮,关闭结点对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会同步显示出该结点。其余结点的 输入类似。 (2)单元定义 在结点定义命令后面的是单元定义命令。此时,要用到虚拟刚结点的概念。第一行单元 定义命令为:“单元,1,2,1,1,0,1,1,1”;其中关键词“单元”或“E”后面的 1,2 为单元两端 的结点码;随后的 6 个数据是两端点与虚拟刚结点 1,2 的连接码。用对话框输入该命令步骤 如下: 1) 在“命令”菜单下选择“单元”子菜单,打开单元对话框;此时,默认的命令选择 是单元定义。 2) 单元编码按照输入顺序自动排列,因此没有单元码输入选项。 3) 在“杆端 1”的“连接结点”处输入 1,“连接方式”选“铰结”。 4

S2-4在求解器中输入平面结构体系 4)在“杆端2”的“连接结点”处输入2,“连接方式”选“刚结”。 5)若要预览,可以单击“预览”。 6)单击“应用”按钮,将命令写到文档上,而后可以继续下一个命令。 7)单击“关闭”按钮,关闭对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会显示出该单元。其余单元的输入 类似。在观览器的“显示”菜单中,激活“单元方向”,则在各单元上可以看到表示单元方向 的箭头;在观览器的“标注”菜单中,可以激活或取消“单元长度”、“单元码”等选项。 (3)结点支承定义 在单元定义命令后面的是结点支承定义命令。此时,也要用到虚拟刚结点的概念。第一 行结点支承命令为:“结点支承,1,4,0,0,0”:其中关键词“结点支承”或“NSUPT”后面的1 表示结点1:4代表第4类支承(即第3种铰支座):随后的0代表支座方位为水平放置(无 转动):0,0表示支座无水平和竖向位移。用对话框输入该命令步骤如下: 1)在“命令”菜单下选择“位移约束”子菜单,打开支座约束对话框: 2)默认的约束类型是“结点支座”,在“结点码”下拉框中输入1: 3)在“支座类型”处选4,“支座性质”保留默认的“刚性”,其余的均为0: 4)其余的同单元定义的第5)~7)。 此时,可以在文档上看到命令行,同时观览器中会显示出该支座。最后一行结点支座命令“结 点支承,6,6,0,0,0,0”在末尾多了一个0,这是由于该支座为固定支座,最后一个0表示该支 座无转角
§2-4 在求解器中输入平面结构体系 4) 在“杆端 2”的“连接结点”处输入 2,“连接方式”选“刚结”。 5) 若要预览,可以单击“预览”。 6) 单击“应用”按钮,将命令写到文档上,而后可以继续下一个命令。 7) 单击“关闭”按钮,关闭对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会显示出该单元。其余单元的输入 类似。在观览器的“显示”菜单中,激活“单元方向”,则在各单元上可以看到表示单元方向 的箭头;在观览器的“标注”菜单中,可以激活或取消“单元长度”、“单元码”等选项。 (3) 结点支承定义 在单元定义命令后面的是结点支承定义命令。此时,也要用到虚拟刚结点的概念。第一 行结点支承命令为:“结点支承,1,4,0,0,0”;其中关键词“结点支承”或“NSUPT”后面的 1 表示结点 1;4 代表第 4 类支承(即第 3 种铰支座);随后的 0 代表支座方位为水平放置(无 转动);0,0 表示支座无水平和竖向位移。用对话框输入该命令步骤如下: 1) 在“命令”菜单下选择“位移约束”子菜单,打开支座约束对话框; 2) 默认的约束类型是“结点支座”,在“结点码”下拉框中输入 1; 3) 在“支座类型”处选 4,“支座性质”保留默认的“刚性”,其余的均为 0; 4) 其余的同单元定义的第 5)~7)。 此时,可以在文档上看到命令行,同时观览器中会显示出该支座。最后一行结点支座命令“结 点支承,6,6,0,0,0,0”在末尾多了一个 0,这是由于该支座为固定支座,最后一个 0 表示该支 座无转角。 5

$2-5用求解器进行几何构造分析 S2-5用求解器进行几何构造分析 1.几何构造分析的计算机方法 进行几何构造分析时采用的方法可分为两类:一类是适用于手算的经典方法,另一类是 适用于计算机的程序方法。 在前边的学习中,学到的用三角形组成规律进行几何构造分析的方法是一种适用于手算 的经典方法。这种方法机智灵巧,但不便于编制计算机程序:能够简捷地处理工程中常用的 杆件体系问题,但难于处理复杂的杆件体系问题。 在求解器中自然采用计算机方法。关于这种方法的详细内容将在《程序结构力学》中介 绍,本盘主要将求解器当作工具使用,并对其解题思路作一简述。 思路一一把平面体系的几何构造分析问题表示为一组齐次线性代数方程问题,然后根 据方程组的解的性质可得出几何构造分析的有关结论。 求解步骤: (1)拆除体系中的各个约束,以体系的独立的结点位移作为基本未知量,共有N个。 (2)再把约束加上去,也就是在待求位移之间建立约束条件,得到以N个结点位移为未知 量的M个齐次线性代数方程。 (3)由方程组求解待定位移。根据方程组系数矩阵的阶数和秩,可以确定解的性质。 如方程组有唯一的平凡解(待定位移都是零),则体系为几何不变:反之则为可变。 如方程组系数矩阵的秩小于约束方程的个数,则体系具有多余约束。 2.两种求解模式 对于几何构造分析,求解器具两种求解模式: (1)自动求解 可以对任意的平面体系进行几何构造分析:判断几何可变还是不变:对于可变体系,给 出体系自由度数,指出是常变还是瞬变,并静态或动画显示机构运动模态:若体系有多余约 束,给出多余约束的数目。 (2)智能求解 按两刚片或三刚片法则求解,给出具体的求解步骤。对于无法用三角形法则求解的问题, 给出提示。 自动求解可用来求解所有问题,也是一个方便的研究工具:而智能求解可以模仿人工手 算给出解题思路与步骤,对学生很有帮助。以下通过例题来分别加以说明和介绍。 例2-5-1试用两种求解模式分析图2-5-1a的几何构造,其中结点5、6是组合结点。 解首先,考虑自动求解。输入后的命令文档为 TITLE,例2-5-1 (a) (5) 结点,1,0,0 结点,2,0.4,0 (8) 9) 结点,3,0.6,0 (11)8 结点,4,1,0 (4) (6) 结点,5,0.2,0.5 (7) (10) 结点,6,0.8,0.5 结点,7,0.35,0.3 (1) (2) (3) 结点,8,0.65,0.3 单元,1,2,1,1,0,1,1,0
§2-5 用求解器进行几何构造分析 §2-5 用求解器进行几何构造分析 1. 几何构造分析的计算机方法 进行几何构造分析时采用的方法可分为两类:一类是适用于手算的经典方法,另一类是 适用于计算机的程序方法。 在前边的学习中,学到的用三角形组成规律进行几何构造分析的方法是一种适用于手算 的经典方法。这种方法机智灵巧,但不便于编制计算机程序;能够简捷地处理工程中常用的 杆件体系问题,但难于处理复杂的杆件体系问题。 在求解器中自然采用计算机方法。关于这种方法的详细内容将在《程序结构力学》中介 绍,本盘主要将求解器当作工具使用,并对其解题思路作一简述。 思路 —— 把平面体系的几何构造分析问题表示为一组齐次线性代数方程问题,然后根 据方程组的解的性质可得出几何构造分析的有关结论。 求解步骤: (1) 拆除体系中的各个约束,以体系的独立的结点位移作为基本未知量,共有 N 个。 (2) 再把约束加上去,也就是在待求位移之间建立约束条件,得到以 N 个结点位移为未知 量的 M 个齐次线性代数方程。 (3) 由方程组求解待定位移。根据方程组系数矩阵的阶数和秩,可以确定解的性质。 如方程组有唯一的平凡解(待定位移都是零),则体系为几何不变;反之则为可变。 如方程组系数矩阵的秩小于约束方程的个数,则体系具有多余约束。 2. 两种求解模式 对于几何构造分析,求解器具两种求解模式: (1) 自动求解 可以对任意的平面体系进行几何构造分析:判断几何可变还是不变;对于可变体系,给 出体系自由度数,指出是常变还是瞬变,并静态或动画显示机构运动模态;若体系有多余约 束,给出多余约束的数目。 (2) 智能求解 按两刚片或三刚片法则求解,给出具体的求解步骤。对于无法用三角形法则求解的问题, 给出提示。 自动求解可用来求解所有问题,也是一个方便的研究工具;而智能求解可以模仿人工手 算给出解题思路与步骤,对学生很有帮助。以下通过例题来分别加以说明和介绍。 例 2-5-1 试用两种求解模式分析图 2-5-1a 的几何构造,其中结点 5、6 是组合结点。 解 首先,考虑自动求解。输入后的命令文档为 TITLE,例 2-5-1 结点,1,0,0 结点,2,0.4,0 结点,3,0.6,0 结点,4,1,0 结点,5,0.2,0.5 结点,6,0.8,0.5 结点,7,0.35,0.3 结点,8,0.65,0.3 单元,1,2,1,1,0,1,1,0 1
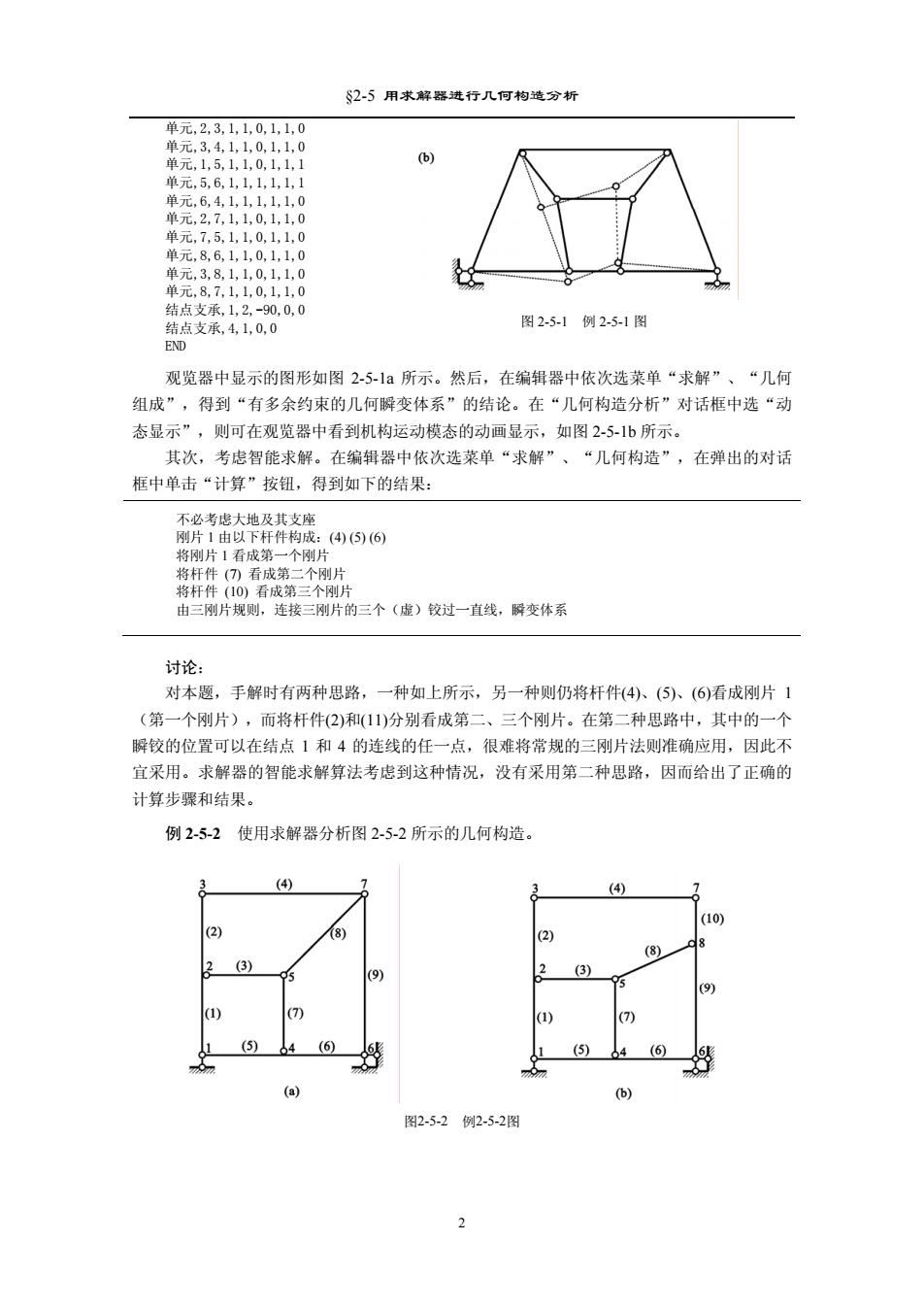
2-5用求解器进行几何构造分析 单元,2,31,1,0,1,1,0 单元,3,4,1,1,0,1,1,0 单元,1,5,1,1,0,1,1,1 单元,5,6,1,1,1,1,1,1 单元,6,4,1,1,1,1,1,0 单元,2,7,1,1,0,1,1,0 单元,7,5,1,1,0,1,1,0 单元,8,6,1,1,0,1,1,0 单元,3,8,1,1,0,1,10 单元,8,7,1,1,0,1,1,0 结点支承,1,2,-90,0,0 结点支承,4,1,0,0 图2-5-1例2-5-1图 END 观览器中显示的图形如图2-5-1a所示。然后,在编辑器中依次选菜单“求解”、“几何 组成”,得到“有多余约束的几何瞬变体系”的结论。在“几何构造分析”对话框中选“动 态显示”,则可在观览器中看到机构运动模态的动画显示,如图2-5-1b所示。 其次,考虑智能求解。在编辑器中依次选菜单“求解”、“几何构造”,在弹出的对话 框中单击“计算”按钮,得到如下的结果: 不必考虑大地及其支座 刚片1由以下杆件构成:(4)(⑤)(6) 将刚片1看成第一个刚片 将杆件()看成第二个刚片 将杆件(10)看成第三个刚片 由三刚片规则,连接三刚片的三个(虚)铰过一直线,瞬变体系 讨论: 对本题,手解时有两种思路,一种如上所示,另一种则仍将杆件(4)、(⑤)、(6)看成刚片1 (第一个刚片),而将杆件(2)和(11)分别看成第二、三个刚片。在第二种思路中,其中的一个 瞬铰的位置可以在结点1和4的连线的任一点,很难将常规的三刚片法则准确应用,因此不 宜采用。求解器的智能求解算法考虑到这种情况,没有采用第二种思路,因而给出了正确的 计算步骤和结果。 例2-5-2使用求解器分析图2-5-2所示的几何构造。 (4) (4) (10) (2) (8) (2) 8 (8) 2 (3) (9) 2 (3) (9) (1) (7) (1) (7) (5) 4 (6) 6 (5) 4 (6) 6 (a) (b) 图2-5-2 例2-5-2图 2
§2-5 用求解器进行几何构造分析 图 2-5-1 例 2-5-1 图 单元,2,3,1,1,0,1,1,0 单元,3,4,1,1,0,1,1,0 单元,1,5,1,1,0,1,1,1 单元,5,6,1,1,1,1,1,1 单元,6,4,1,1,1,1,1,0 单元,2,7,1,1,0,1,1,0 单元,7,5,1,1,0,1,1,0 单元,8,6,1,1,0,1,1,0 单元,3,8,1,1,0,1,1,0 单元,8,7,1,1,0,1,1,0 结点支承,1,2,-90,0,0 结点支承,4,1,0,0 END 观览器中显示的图形如图 2-5-1a 所示。然后,在编辑器中依次选菜单“求解”、“几何 组成”,得到“有多余约束的几何瞬变体系”的结论。在“几何构造分析”对话框中选“动 态显示”,则可在观览器中看到机构运动模态的动画显示,如图 2-5-1b 所示。 其次,考虑智能求解。在编辑器中依次选菜单“求解”、“几何构造”,在弹出的对话 框中单击“计算”按钮,得到如下的结果: 不必考虑大地及其支座 刚片 1 由以下杆件构成:(4) (5) (6) 将刚片 1 看成第一个刚片 将杆件 (7) 看成第二个刚片 将杆件 (10) 看成第三个刚片 由三刚片规则,连接三刚片的三个(虚)铰过一直线,瞬变体系 讨论: 对本题,手解时有两种思路,一种如上所示,另一种则仍将杆件(4)、(5)、(6)看成刚片 1 (第一个刚片),而将杆件(2)和(11)分别看成第二、三个刚片。在第二种思路中,其中的一个 瞬铰的位置可以在结点 1 和 4 的连线的任一点,很难将常规的三刚片法则准确应用,因此不 宜采用。求解器的智能求解算法考虑到这种情况,没有采用第二种思路,因而给出了正确的 计算步骤和结果。 例 2-5-2 使用求解器分析图 2-5-2 所示的几何构造。 图2-5-2 例2-5-2图 2