
第二部分组合变形 第七章应力状态分析(2) 第八章强度理论() 第九章组合变形(2) 阶段复习与习题课() 西半究通大¥ XIAN JIAOTONG UNIVERSITY 航天航空学院-力学中心
第二部分 组合变形 第七章 应力状态分析 (2) 第八章 强度理论 (1) 第九章 组合变形 (2) 阶段复习与习题课 (1) 航天航空学院--力学中心

第七章应力状态分析 应力状态的概念 二向应力状态分析一公式解析法 ■ 二向应力状态分析一图解解析法 ■ 典型的三向应力状态 ■ 广义胡克定律 ■ 平面应力状态下的应变分析 西步充通大率 XIAN JIAOTONG UNIVERSITY 航天航空学院-力学中心心
第七章 应力状态分析 应力状态的概念 二向应力状态分析 —公式解析法 二向应力状态分析 —图解解析法 典型的三向应力状态 广义胡克定律 平面应力状态下的应变分析 * 航天航空学院--力学中心
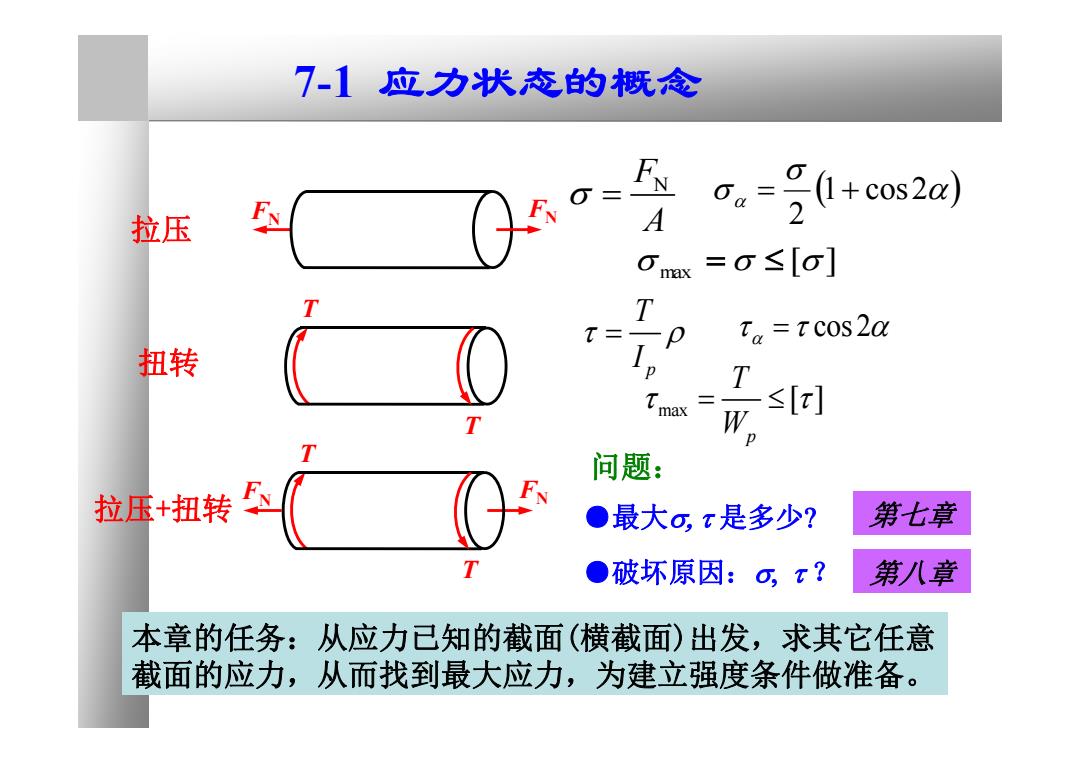
7-1应力状态的概念 。=g+cos2a 拉压 A Ox=O≤[o] T T= t,=tcos2a 扭转 I T max ≤[] W 问题: 拉压+扭转 ●最大ox是多少? 第七章 ●破坏原因:o,x? 第八章 本章的任务:从应力已知的截面(横截面)出发,求其它任意 截面的应力,从而找到最大应力,为建立强度条件做准备
拉压 FN A 1 cos2 2 [ ] max 扭转 p T I cos 2 max [ ] p T W 拉压+扭转 问题: ●破坏原因: ? ●最大 是多少 本章的任务:从应力已知的截面(横截面)出发,求其它任意 截面的应力,从而找到最大应力,为建立强度条件做准备。 7-1 应力状态的概念 第七章 第八章 FN FN T T FN FN T T

7-1应力状态的概念 应力状态的概念: ● 通过同一点所取截面方向不同,应力的大小也不同。应 力既是点的位置的函数,也是过该点的截面方位的函数。 ● 通过同一点不同方位截面上的应力的集合称为该点的 应力状态(Stress State)。 ● 材料力学中的“点”是物理点,不是几何点,有大小和形 状,通常用正六面体表示,称为单元体(Element Volume)。 单元体很小,可以认为: (1)各个面上的应力均匀分布; (2)相互平行的平面上,应力大小和性质完全相同
● 材料力学中的“点”是物理点,不是几何点,有大小和形 状,通常用正六面体表示,称为单元体 (Element Volume) 。 ● 通过同一点所取截面方向不同,应力的大小也不同。应 力既是点的位置的函数,也是过该点的截面方位的函数。 ● 通过同一点不同方位截面上的应力的集合称为该点的 应力状态(Stress State) 。 应力状态的概念: ● 单元体很小,可以认为: (1)各个面上的应力均匀分布; (2)相互平行的平面上,应力大小和性质完全相同。 7-1 应力状态的概念
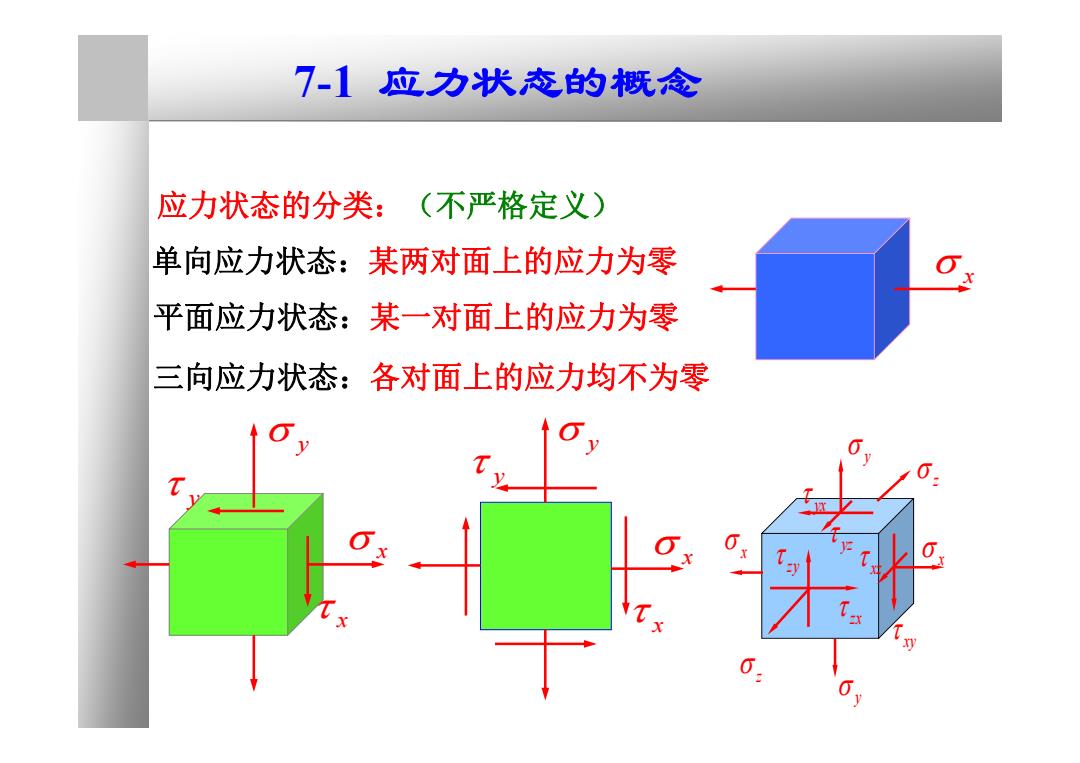
7-1应力状态的概念 应力状态的分类: (不严格定义) 单向应力状态:某两对面上的应力为零 平面应力状态:某一对面上的应力为零 三向应力状态:各对面上的应力均不为零
应力状态的分类:(不严格定义) 平面应力状态:某一对面上的应力为零 三向应力状态:各对面上的应力均不为零 x y y x x y y x 单向应力状态:某两对面上的应力为零 x xy x y z y z x yx zy zx yz xz 7-1 应力状态的概念

7-2二向应力状态分析一公式解析法 己知:Ox,Oy,Tx=-ty, 求:任意斜截面上应力 a:截面外法线n与x轴之间的夹角, x到n逆针向转动为正。 A,=Acosa A,=Asi >F=0 aA-o,A,cosa-oA,sin a+ +t,4,sin a+,4,cosa=0 >F=0 taAa-o 4,sin a+o4,cosa+ -t,4.cosa+t,A,sin a=0 x+y cos2a-t,sin 2a sin 2a+t,cos2a 2 2 Ta= 2
求:任意斜截面上应力 x y x y x y x n y x y x :截面外法线 n 与 x 轴之间的夹角, x 到 n 逆针向转动为正。 已知: , , , x y x y Ax A cos , A y Asin 0 Fn A xAx cos yAy sin sin cos 0 xAx yAy 0 F A xAx sin yAy cos cos sin 0 xAx yAy cos2 sin 2 2 2 x x y x y sin 2 cos2 2 x x y 7-2 二向应力状态分析—公式解析法

7-2二向应力状态分析一公式解析法 0+0y」 -cos2a-t,sin 2a Ta= sin 2a+t.cos2a 2 2 2 最大和最小正应力 切应力为零的面为主平面 tan 2%o -2tx时: (Principal Planes); 主平面上的正应力为主应 力Principal Stress); max 2+ 全部由主平面构成的单元 2 体为主单元体。 此时: Tao =0 最大和最小切应力 tan 2a=- x一时: 2t, =+ 极值切应力平面与主平面的夹角为45°: 01=0±45 0a+90+0a=0x+0yTa+90=-Ta
cos 2 sin 2 2 2 x x y x y sin 2 cos 2 2 x x y ● 最大和最小正应力 2 2 min max ) 2 ( 2 x x y x y 0 2 tan 2 x x y 时: ● 最大和最小切应力 2 2 min max ) 2 ( x x y 1 tan 2 2 x y x 时: 此时: 0 0 切应力为零的面为主平面 (Principal Planes) ; 主平面上的正应力为主应 力(Principal Stress) ; 全部由主平面构成的单元 体为主单元体 。 ● 极值切应力平面与主平面的夹角为45°: 45 1 0 90 x y ● 90 7-2 二向应力状态分析 —公式解析法

7-2二向应力状态分析一公式解析法 例从工字钢悬臂梁的固定端A点取出单元体如图所示。 己知:ox=70MPa,o,=0,tx=50MPa 求:a=30°截面的正应力和切应力,主应 力的大小和主平面方位及最大切应力 解:根据公式,得 70.70 cos60°-50sin60°=9.2MPa 2 2 67.5° 70 Ta in60°+50cos60°=55.3MPa 2 -27.5 2×50 0=-27.5° 主平面 tan 20o -70 4'=67.5° 最大切应力 主应力 01=0-275=96MPa 02=0675=-26MPa tmx=V(35)2+502=61MPa
例 从工字钢悬臂梁的固定端 A 点取出单元体如图所示。 已知: 70MPa, 0, 50MPa x yx A x x 解: 主平面 0 2 50 tan 2 70 27.5 0 ' 67.5 0 27.5 67.5 1 27.5 96MPa 2 67.5 26MPa 1 2 sin 60 2 70 50cos60 55.3MPa 70 70 cos 60 50 sin 60 9.2MPa 2 2 根据公式,得 2 2 max (35) 50 61MPa 求: α=30 º截面的正应力和切应力,主应 力的大小和主平面方位及最大切应力 主应力 最大切应力 7-2 二向应力状态分析 —公式解析法

7-3二向应力状态分析一图解解析法 0a= 2 ,-o cos2a-t,sin 2a 2 Ta x-y sin 2a+t,cos2a 2 消去参数a,得 +-色,y+=R 2 圆心: +2,0) 半径: R=1 y 2 2 应力圆(莫尔圆),是德国科学家Mohr在1882年最先提出的
2 2 2 2 2 ) 2 ) ( 2 ( x R x y x y 圆心: , 0) 2 ( x y 半径: 2 2 ) 2 ( x x y R cos2 sin 2 2 2 x x y x y sin 2 cos2 2 x x y 消去参数α,得 应力圆(莫尔圆),是德国科学家Mohr在1882年最先提出的。 7-3 二向应力状态分析—图解解析法
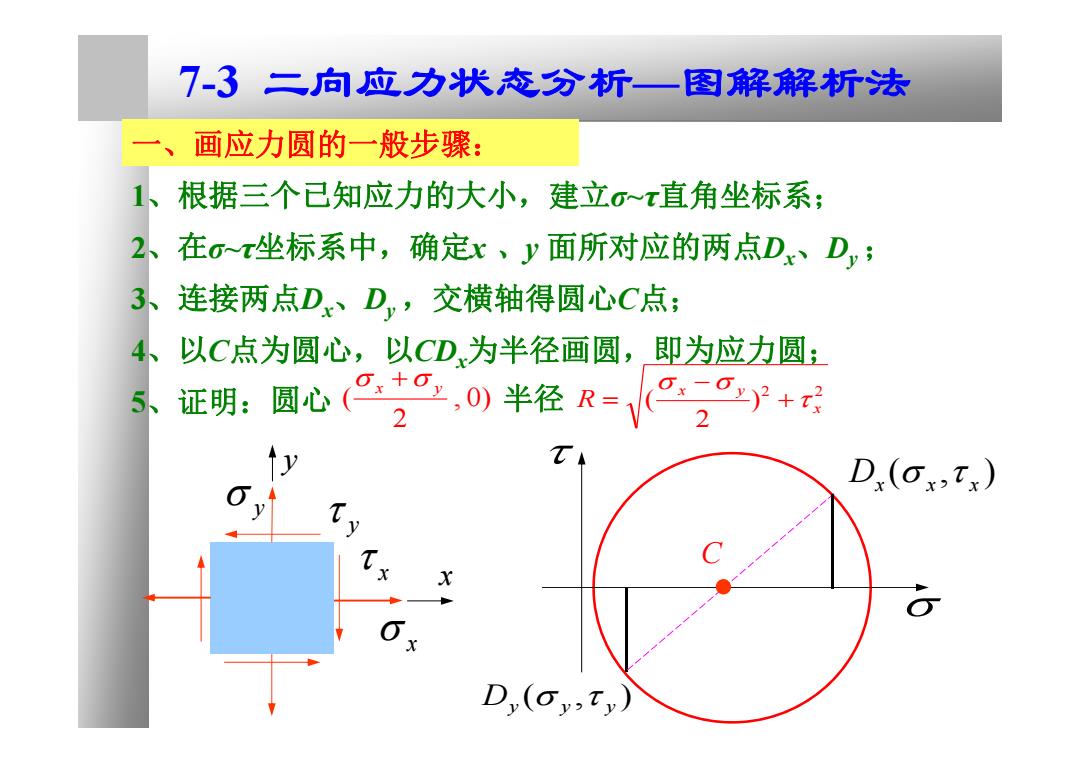
门-3二向应力状态分析—图解解析法 一、 画应力圆的一般步骤: 1、根据三个已知应力的大小,建立o~x直角坐标系; 2、 在o坐标系中,确定x、y面所对应的两点D、D; 3、 连接两点D、D,交横轴得圆心C点; 4、以C点为圆心,以CD为半径画圆,即为应力圆: 5、 证明:圆心0)半径R- ,-) 2 D.(OxTx) X D(oy,ty))
x y x y x y ( , ) Dy y y C ( , ) Dx x x 一、画应力圆的一般步骤: 1、根据三个已知应力的大小,建立σ~τ直角坐标系; 2、在σ~τ坐标系中,确定x 、y 面所对应的两点Dx、Dy ; 3、连接两点Dx、Dy ,交横轴得圆心C点; 4、以C点为圆心,以CDx为半径画圆,即为应力圆; 5、证明:圆心 , 0) 半径 2 ( x y 2 2 ) 2 ( x x y R 7-3 二向应力状态分析—图解解析法