
Inverse Dynamic Analysis of Double Pendulum X2 M2 M M R Link Bi is connected to the ground with revolute joint O,connect to B2 with revolute joint A. Given parameters: m1=m2=m,1=l2=1,m=1kg,1=1m Driving constraint equation:4=πt,4,-4=πt Calculate time histories of Rs,R,M,M2 Initial estimate: Constraint equation 1 x-cos 1 y-sin y )cos2-x1 -cos ,9= 1 1 y2 inysin y 41-π1 2] 42-4,-πt
Inverse Dynamic Analysis of Double Pendulum Link B1 is connected to the ground with revolute joint O, connect to B2 with revolute joint A. Given parameters: m1 m2 m , 1 2 l l l , m 1 kg , l 1m Driving constraint equation: 1 2 1 t, t Calculate time histories of 1 1 1 2 , , , R x R y M M Initial estimate: T l l 0 0 2 3 0 0 2 1 q(0) Constraint equation t t l y l y l x l x l y l x 2 1 1 2 2 1 1 2 2 1 1 1 1 1 1 sin 2 sin 2 cos 2 cos 2 sin 2 cos 2 , 2 2 2 1 1 1 y x y x q

1 1 0 sin 00 2 01 c0s400 0 1 ,= -10 -sin 1 0 2 sin 0-1- 2cos 01- c0s4 0 0 1 00 0 L00 -1 00 1 152 07 cos 1 -。4,sin4, 2 V= 0 ,Y= 02cos L sin 2 0 0 m 07 m -mg ml2/12 Q4= 0 M= m 0 m -mg ml2/12 0 D,'=2-Mi R=-,R,=-入2,M1=-,M2=- Flow chart
0 0 1 0 0 1 0 0 1 0 0 0 cos 2 cos 0 1 2 0 1 sin 2 sin 1 0 2 1 0 cos 0 0 0 2 0 1 sin 0 0 0 2 1 0 1 2 1 2 1 1 l l l l l l q 0 0 0 0 V , 0 0 sin 2 sin 2 cos 2 cos 2 sin 2 cos 2 2 2 1 2 2 1 2 2 1 2 2 1 1 2 1 1 2 1 l l l l l l /12 /12 2 2 ml m m ml m m M , 0 0 0 0 mg mg A Q Q Mq q T A 1 1 1 2 1 5 2 6 , , , R x R y M M Flow chart
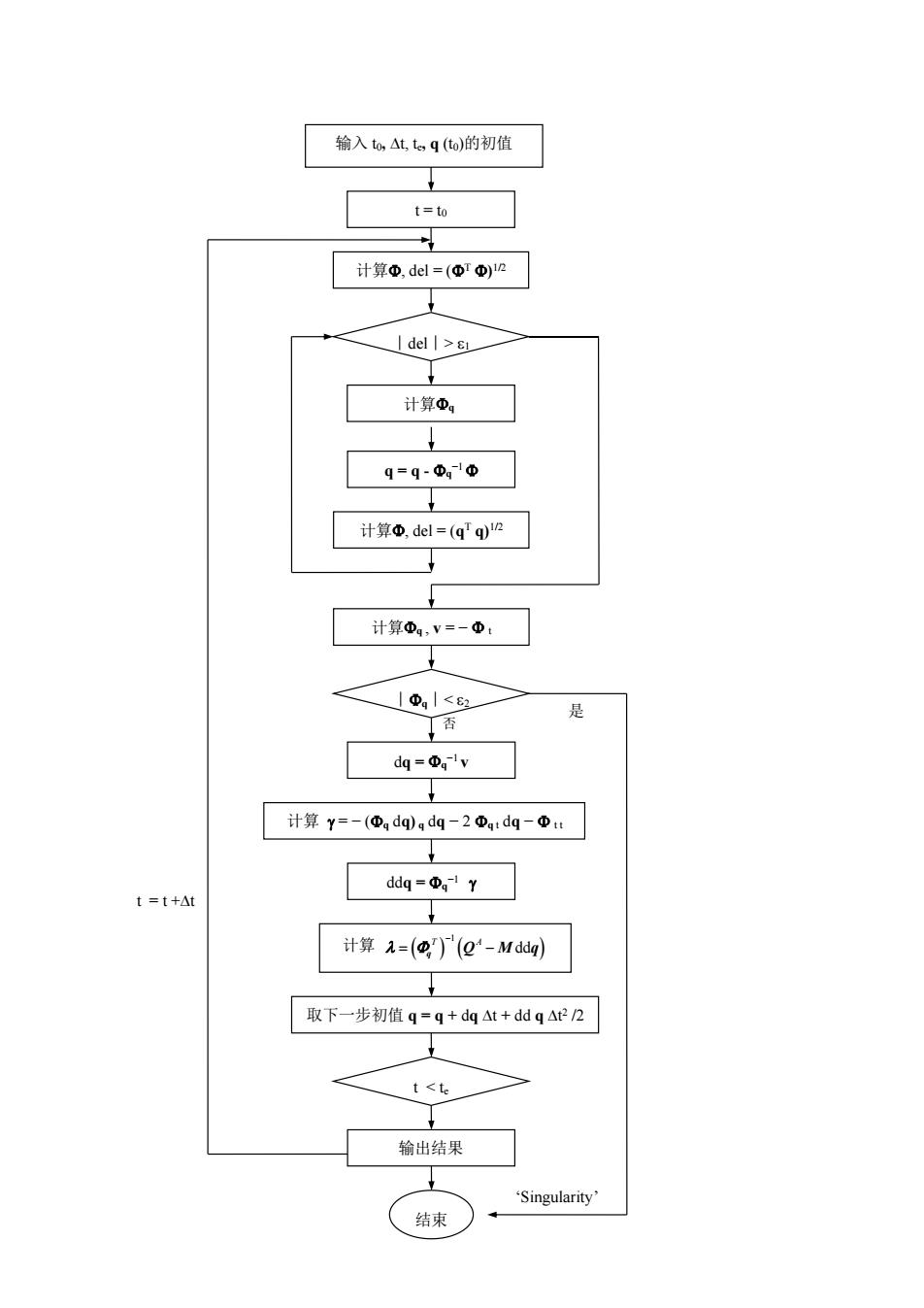
输入to,△tt,q(to)的初值 t=to 计算Φ,del=(ΦTΦ)2 I del I> 计算Φ, q=q-0g10 计算Φ,del=(gTq)n 计算Φa,V=-Φ: |Da|<82 是 香 dq=Φg1v 计算Y=-(④gdq)gdg-2Φgtdg-t ddg=Φg1Y t=t+At 计算=()(g-Mdg) 取下一步初值q=q+dq△t+ddq△t22 t<te 输出结果 ‘Singularity' 结束
t = t0 计算, del = (T ) 1/2 ∣del∣> 1 计算q q = q -q−1 计算, del = (q T q) 1/2 计算q , v = − t ∣q∣< 2 dq = q−1 v 计算 = − (q dq) q dq −2 q t dq − t t ddq = q−1 取下一步初值 q = q + dq t + dd q t2 /2 t < te 输出结果 结束 ‘Singularity’ t = t +t 输入 t0, t, te, q (t0)的初值 是 否 计算 1 dd T A q Q M q