上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Modeling for Example 5

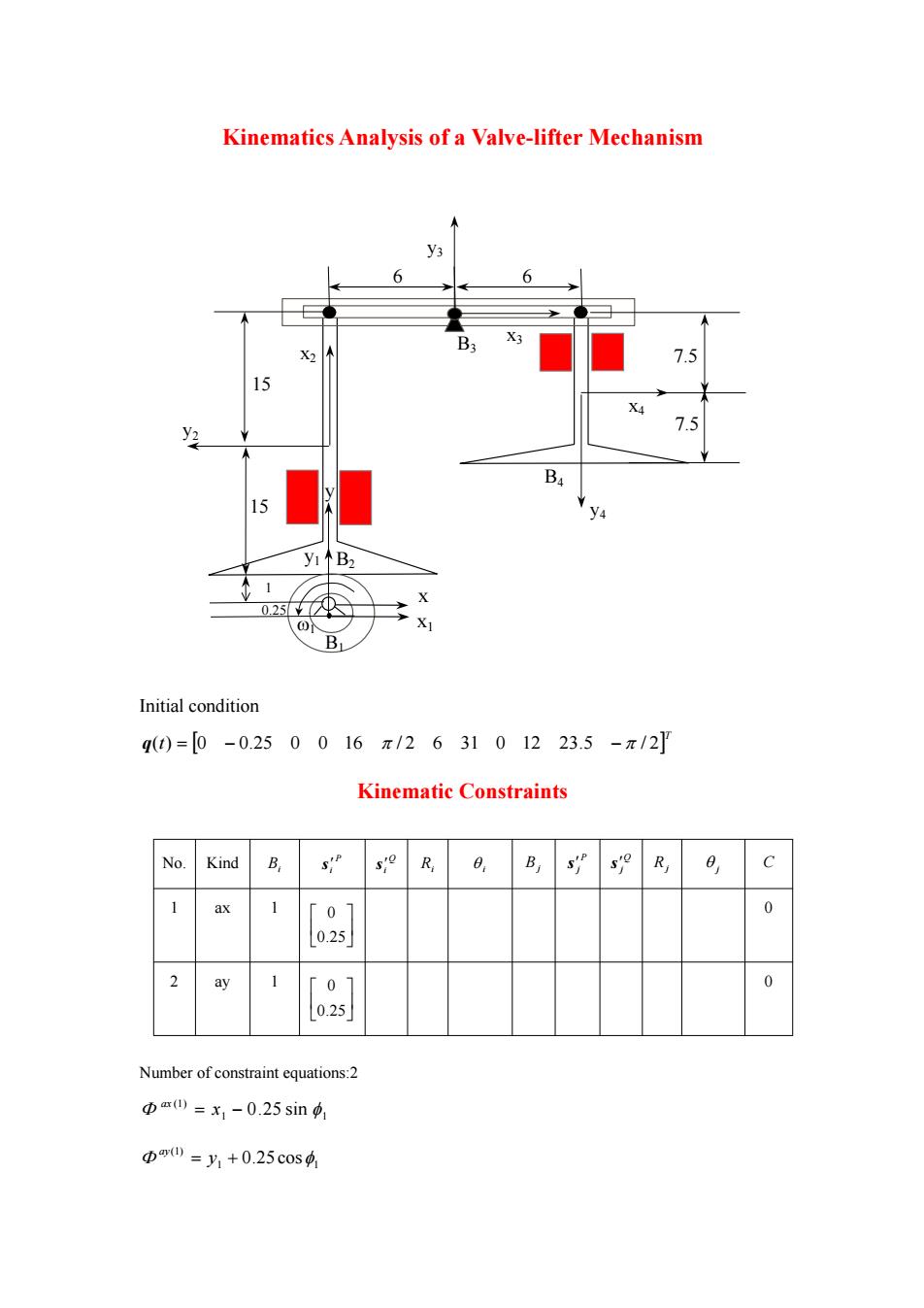
Kinematics Analysis of a Valve-lifter Mechanism y3 6 6 B3 X3 2 7.5 15 y2 7.5 B 15 A y1个B2 0.257 ) Initial condition q0=[0-0.250016π/263101223.5-π/2 Kinematic Constraints No. Kind 足 sio 0, so R, 8, C 1 ax 1 01 0 0.25 2 ay 0 0 0.25 Number of constraint equations:2 Φmm=x1-0.25sin91 Φm0=y1+0.25c0s4

Kinematics Analysis of a Valve-lifter Mechanism B4 B3 x B1 x2 B2 1 0.25 1 15 6 7.5 6 y x1 y1 y2 x3 y3 15 7.5 y4 x4 Initial condition   T q(t)  0  0.25 0 0 16  / 2 6 31 0 12 23.5   / 2 Kinematic Constraints No. Kind Bi P i s Q i s Ri  i B j P j s Q j s R j  j C 1 ax 1       0.25 0 0 2 ay 1       0.25 0 0 Number of constraint equations:2 1 1 (1)   x  0.25 sin  ax 1 1 (1)   y  0.25 cos ay

No. Kind B '9 R R ax 2 0 o a帥 2 π/2 Number of constraint equations:2 Φm(2)=X2 3=4-2 No. Kind B 心 o R 9 B, R C cff 1 To 1.25 0 Number of constraint equations:1 1,2) (B,4)P-】 gBu where -[] B2=RA12= 「-sin(p2-)-cos(2-4) cos(2-4,) -sin(p2-,)」 =--[9 gB45=sin(02-4-a,） [-] n"-r=n+A(sio+pui)-n-As2e,ui= cOS 1 p1=1.25 sin a x1-x2+1.25cos(4+a1)+15cos42 --为+125sm6+a+15sn」

No. Kind Bi P i s Q i s Ri  i B j P j s Q j s R j  j C 3 ax 2       0 0 0 4 a 2 /2 Number of constraint equations:2 2 ( 2 ) x ax   2 2 (2)       aNo. Kind Bi P i s Q i s Ri  i B j P j s Q j s R j  j C 5 cff 1       0 0 1.25 2       1 15       0 15 Number of constraint equations:1                1 12 2 (1,2 ) 2 2 1 2 g B u B u r r T T P Q cf  where         1 1 1 cos sin   g ,                        2 1 2 1 2 1 2 1 12 12 cos sin sin cos         B RA ,             1 0 2 2 2 Q P u s s ,   1 12 2 2 1 1 g B u  sin      T                         2 2 2 2 2 2 2 2 sin cos 1 0 cos sin sin cos       B u   P Q Q Q 1 2 1 1 1 1 1 2 2 2 r  r  r  A s   u  r  A s ,         1 1 1 sin cos   u , 1.25  1                                                             1 2 1 1 2 1 2 1 1 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 2 1.25 sin 15 sin 1.25 cos 15 cos 0 15 sin cos cos sin sin cos sin cos cos sin 1.25                 y y x x y x y x P Q r r

(B,45)Y(P-r2)=cos4(x1-x2)+sin,(y-y2)+1.25cos(2-4-a)+15 0a-[s46-)+m25o低-4-a)+15-0 sin (2-a) Substitute d2-d-a=0 into cosp2(x1-x2)+sin42(by1-y2)+1.25cos(p2-4,-a1)+15=0 the constraint equation is → DW4,2)=cos2(x1-x2)+sin2by,-y2)+16.25=0 No Kind B, sip e R B R 8, C 6 ax 3 o1 6 7 92 3 31 Number of constraint equations:2 Φm(3)=x3-6 Φm3)=y3-31 No. Kind B siP s° R B, R C ax [01 12 9 aψ 4 -π/2 Number of constraint equations:2 Φ(4)=x4-12 D)=中4+

    cos   sin   1.25 cos   15 2 2 1  2   2 x1  x2   2 y1  y 2   2  1   1  T P Q B u r r          0                  2 1 1 (1,2 ) 2 1 2 2 1 2 2 1 1 sin cos sin 1.25 cos 15    cf  x x  y y     Substitute 0  2  1   1  into cos   sin   1.25 cos   15 0  2 x1  x2   2 y1  y 2   2  1   1   the constraint equation is cos   sin   16 .25 0 2 1 2 2 1 2 (1,2 )  x  x  y  y   cf    No. Kind Bi P i s Q i s Ri  i B j P j s Q j s R j  j C 6 ax 3       0 0 6 7 ay 3       0 0 31 Number of constraint equations:2 6 3 (3)  x  ax  3 31 (3)  y  ay  No. Kind Bi P i s Q i s Ri  i B j P j s Q j s R j  j C 8 ax 4       0 0 12 9 a 4 /2 Number of constraint equations:2 12 4 ( 4 )  x  ax  2 4 (4)       a

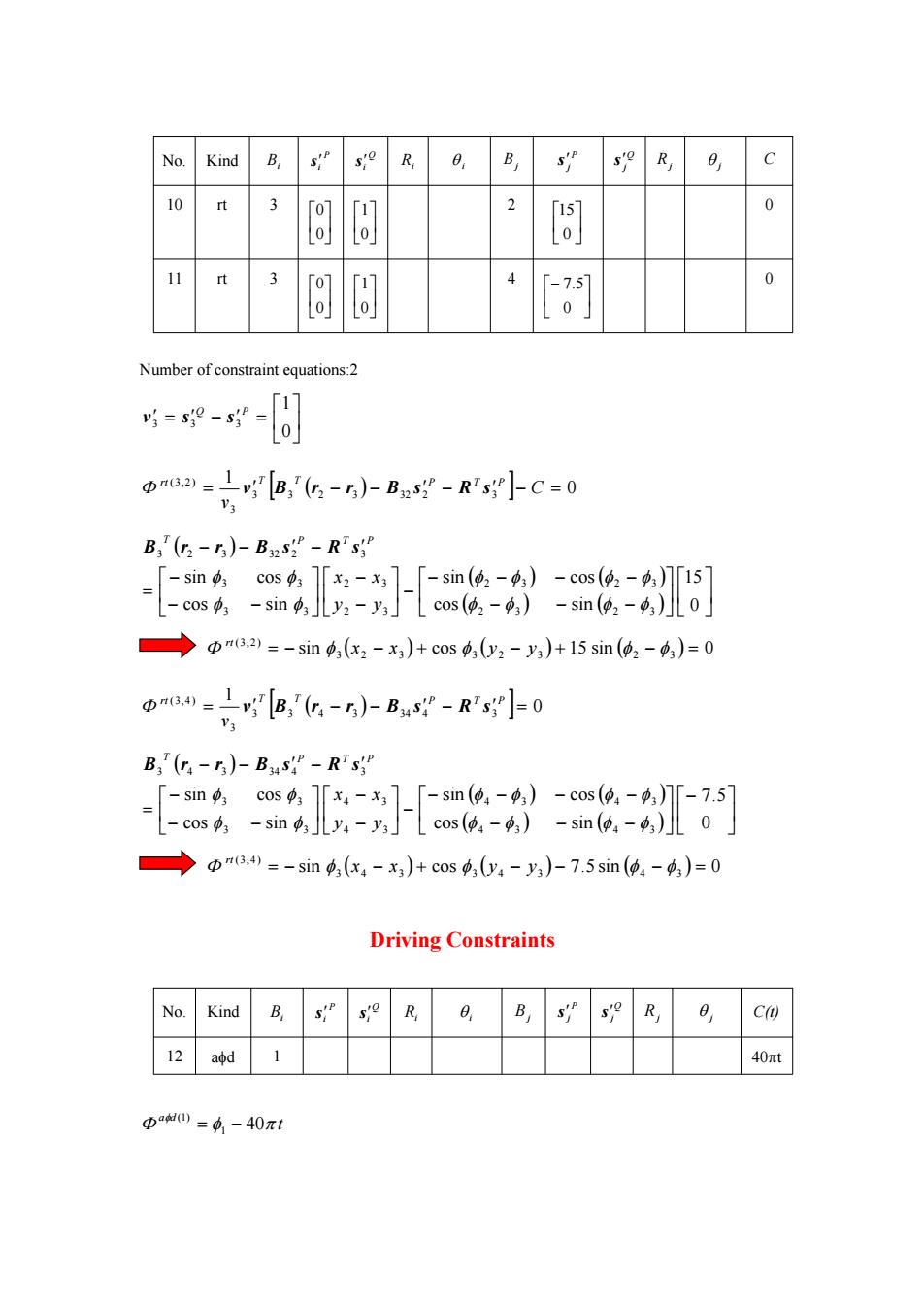
No. Kind B R 0, R, C 10 rt 3 2 T151 0 Lo] 11 3 T0] 4 7.5 0 0 0 Number of constraint equations:2 =s9-s 「17 Dm6)=g7[B,'6,-5)-Bs”-R's]C=0 B:(r2-r)-Bas2-R'ss cos(2-) → Φm6,2)=-sin,(x2-x3)+cos,by2-y3)+15sin(p2-4)=0 Φn6)=1g7[B,6-5)-B4s-R']0 B3 (ra-r)-Baasi -RTss -[m cos(04-4) → Dm6,4)=-sin(x4-x3)+cos0y4-y3)-7.5sin(p4-)=0 Driving Constraints No. Kind B R B R 8, C) 12 aod 1 40πt Φ0=4，-40π1

No. Kind Bi P i s Q i s Ri  i B j P j s Q j s R j  j C 10 rt 3       0 0       0 1 2       0 15 0 11 rt 3       0 0       0 1 4       0 7.5 0 Number of constraint equations:2             0 1 3 3 3 Q P v s s     0 1 3 3 2 3 32 2 3 3 (3,2 )         C  v rt T T P T P  v B r r B s R s                                                    0 15 cos sin sin cos cos sin sin cos 2 3 2 3 2 3 2 3 2 3 2 3 3 3 3 3 3 2 3 32 2 3             y y x x T P T P B r r B s R s sin   cos   15 sin   0 3 2 3 3 2 3 2 3 (3,2 )     x  x   y  y      rt     0 1 3 3 4 3 34 4 3 3 (3,4 )         rt T T P T P v  v B r r B s R s                                                    0 7.5 cos sin sin cos cos sin sin cos 4 3 4 3 4 3 4 3 4 3 4 3 3 3 3 3 3 4 3 34 4 3             y y x x T P T P B r r B s R s sin   cos   7.5 sin   0 3 4 3 3 4 3 4 3 (3,4 )     x  x   y  y      rt Driving Constraints No. Kind Bi P i s Q i s Ri  i Bj P j s Q j s Rj  j C(t) 12 ad 1 40t t a d     40 1 (1)  