上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.5-Driving constraint

3.5 Driving constraint In addition to kinematic structure,the motion of mechanism is described by actuator inputs that specifies the time history of some position coordinates or the relative position of pairs of bodies. To uniquely determine the time history of motion of a mechanism,a number of inputs must be specified,equal in number of degrees of freedom of the system. Driving constraints are family of standard drivers

3.5 Driving constraint • In addition to kinematic structure, the motion of mechanism is described by actuator inputs that specifies the time history of some position coordinates or the relative position of pairs of bodies. • To uniquely determine the time history of motion of a mechanism, a number of inputs must be specified, equal in number of degrees of freedom of the system. • Driving constraints are family of standard drivers

3.5.1 Absolute Drivers Absolute position Driver Φad0=x-C1=x,+x”cos4,-y"sin4,-C()=0 出a=0-x-"cos4 yaxd()=C(t) C2y+G0 Xi +C (t) a0卡y-C, /cos4,C2()=0 =乙co-sirj v(=C2(t) X yo=y0+C,(0）=(sin4+Sr8s4)02+C,(0)

3.5.1 Absolute Drivers x i x  i y y  Pi P ir ir P i s C1(t) C2(t) cos sin ( ) 0 1 1 ( )  x C  x  x   y  i C t  P i i P i i P i axd i     i P i i P i axd i x y i 1 0 sin cos ( )      q ( ) 1 ( ) v C t axd i   ( ) ( cos sin ) ( ) 1 2 1 ( ) ( ) C t x y C t i i P i i P i axd i ax i                sin cos ( ) 0 2 2 ( )  y C  y  x   y  i C t  P i i P i i P i ayd i     i P i i P i ayd i x y i 0 1 cos sin ( )     q ( ) ( sin cos ) ( ) 2 2 2 ( ) ( ) C t x y C t i i P i i P i ayd i ay i                ( ) 2 ( ) v C t ayd i   Absolute position Driver

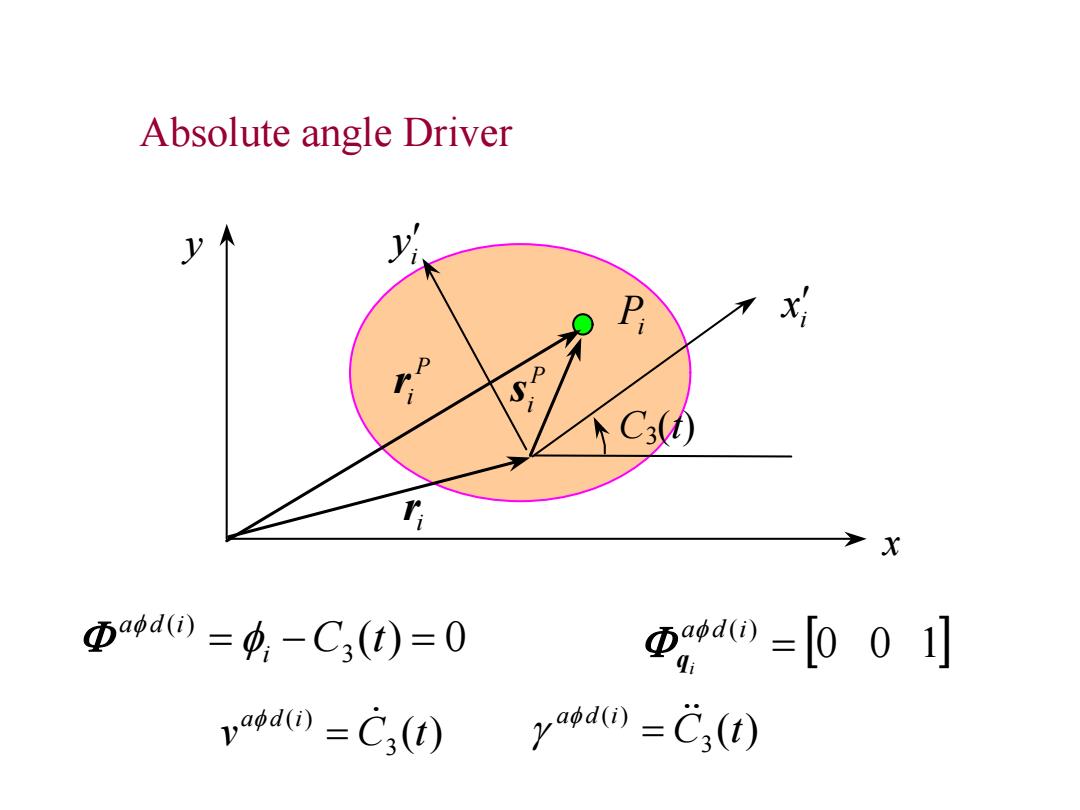
Absolute angle Driver P x C3④ X Φawdo=p,-C3(t)=0 电，do=[00刂 v0d@=C3(t) ya()=C(t)

3 ( ) 0 ( )  i C t  a d i    0 0 1 ( )  a d i i  q ( ) 3 ( ) C t a d i    ( )  3 ( ) v C t a d i    x i x  i y y  Pi P ir ir P i s C3(t) Absolute angle Driver

3.5.2 Constraints between pairs of bodies (Relative constraints) A relativeΦdriver Φrd》=中，-9，-C3()=0 Φgaw=[00] Dw》=[00-] v'aa》=C3(t)） yd(iD=C(t)

3.5.2 Constraints between pairs of bodies (Relative constraints) 3 ( ) 0 ( , )  j  i C t  r d i j     0 0 1 ( , )  r d i j j  q 0 0 1 ( , )   r d i j i  q ( ) 3 ( , ) v C t r d i j    ( ) 3 ( , ) C t r d i j     A relative  driver

A relative distance driver 西》=(-ry(-r）-C4()2=0 》=2-Y(-ryBs] Φ》=2(P-ry-(-yB, v=2C4(t)C4(t) y=y+2C4(t)C4(t)+2[C4(t)] =20-62AsP-,2As）-26-y(-） +2C4(t)C4(t)+2[C4(t)]2

A relative distance driver     ( ) 0 2 4 ( , )    C t  P j P i T P j P i rdd i j  r r r r      P i i T P j P i T P j P i rdd i j i r r r r B s q  2    ( , )        P j j T P j P i T P j P i rdd i j j r r r r B s q  2      ( , )          2 4 4 4 2 2 2 4 4 4 2 ( ) ( ) 2[ ( )] 2 2 2 ( ) ( ) 2[ ( )] C t C t C t C t C t C t P j P i T P j P i P j j j P i i i T P j P i rdd rd                        r r  A s  A s r r r r   2 ( ) ( ) 4 4 v C t C t rdd  

A revolute-rotational driver Φrdw》=(p+0,)-(9,+0,)-C()=0 》=[001 x y C(1) Φga-[00-1 vmau,》=C(t) 分 yrd》=C(t) X

( ) ( ) ( ) 0 ( , )  j  j  i  i C t  rr d i j      0 0 1 ( , )  rrd i j j q 0 0 1 ( , )   rr d i j qi  ( ) ( , ) v C t rrd i j   ( ) ( , ) C t rr d i j    A revolute-rotational driver

A translational-distance driver y, C(t)is the time history of the directed distance di x between P;and P Dn=/4-C0）=0 Vi >x y,=Ad=r+A,”-r-As” Φ》=A,'(-r)+yA,s-ys”-vC()=0

( ) 0 ( , )  C t  vi ij T tdd i j i v d  A translational-distance driver C(t) is the time history of the directed distance between Pi and Pj ( ) ( ) 0 ( , )           viC t  P i T i P ij j T j i i T i T i tdd i j  v A r r v A s v s i i i v  Av P i i i P ij j j j d  r  A s  r  A s

Differentiation of Φ》=4(-)+As-ys”-y,C()=0 One obtains D=A(g-)+A,T(G-)+A,s-,C0） =,yB,(y-)+A,(店-)+B,s(0-,)-vC() =yB,(g-r)+A'(G-)-,C()=0 变》=【yAB'g,-r小，Φ=A0 vaaa,》=v,C(t)

( ) ( ) 0 ( , )           viC t  P i T i P ij j T j i i T i T i tdd i j  v A r r v A s v s ( ) ( ) ( ) 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( , )                              v C t v C t v C t j i i T i T j i i T i T i i j i i P ij j T j i i T i T j i i T i T i i i P ij j T j i i T i T j i i T i T i tdd i j                 v B r r v A r r v B r r v A r r v B s v A r r v A r r v A s      Differentiation of One obtains    0 T i T i tdd i j j i T i T i T i T i tdd i j i j q   v A v B r  r q  v A ( , ) ( , )  ( )   ( ) ( , ) v v C t i tdd i j  

Differentiation of Φ》=，yB,(g-r)+yA(G-)-v,C()=0 One obtains a0=yB,(g-r)-,2yA(y,-r)+2,yB,(G-) +A(-)-y,C()=0 ya》=,2yA(y-r)-2,yB,(G-)+v,C(t)

Differentiation of One obtains ( ) ( ) ( ) 0 ( , )      j  i  viC t  T i T j i i T i T i i tdd i j        v B r r v A r r ( ) ( ) 0 ( ) ( ) 2 ( ) ( , ) 2               v C t j i i T i T i j i T i T j i i i T i T j i i i T i T i i tdd i j          v A r r   v B r r  v A r r  v B r r ( ) 2 ( ) ( ) ( , ) 2 v C t j i i T i T j i i i T i T i i tdd i j         v A r  r   v B r  r 

3.5.3 Right side of velocity and acceleration equations For a kinematic constraint Φ(q=0 The associated driver is of the form Φa(q,t)=Φ(q)-C(t)=0 One obtains ①g=Φ， v4=v+C(t)=C(t) y4=x+C(t)

For a kinematic constraint The associated driver is of the form (q)  0 3.5.3 Right side of velocity and acceleration equations ( ,t)  ( )  (t)  0 d  q  q C One obtains q q d (t) (t) d v v C C    (t) d C    