
6.6 Constraint reaction forces Variational equation ,(M,+西,7-0)=0 i=l virtual work of all the constraint forces acted on body i o,=西…l=立a"天 =[2…水…m] Consider the k th joint -,'水— virtual work of the constraint forces of the kth constraint acted on body i
6.6 Constraint reaction forces ( ) 0 1 n i A i T i i T i i q M q q Q Variational equation T k nh nh l l T T l i T nh Tk T T i T T i i i i i i 1 1 1 q q q q q q q q Consider the k th joint T T i i q q virtual work of all the constraint forces acted on body i virtual work of the constraint forces of the kth constraint acted on body i k T T k i i q q

Virtual work of the constraint forces of the k th constraint acted on body i 面Q}女ook r=r+As”,m,”=+B,s'6动 > m=6m-B,s6冲, m=-6,更'+动,更h =-m,更,+60,sB,水-64,Φ
k T k i T T k i k T k Tk i T i k T T k i i i i i W i r r q q r r Virtual work of the constraint forces of the k th constraint acted on body i i P i i i P i P i i i P ri r A s , r r B s k T k i k T T k i T P i i k Tk T P i k T k i T T k i i i i W i i r r r r s B r i P i i P ri ri B s

y PP X ER Tk Constraint force vector and torque with respect to o-xy Virtual work of the constraint forces of the k th constraint acted on body i can be written as δW=(6r,P)TF+60,T equal to w=-m2+δ动,spB,更-60,Φ' Fk =-AI T=yPB,更-西2
k i i k i P T W (ri ) F T Virtual work of the constraint forces of the k th constraint acted on body i can be written as k i k Fi , T Constraint force vector and torque with respect to o-xy P Fik riP riP i Tik x y k T k i k T T k i T P i i k Tk T P i W i i i r r s B r equal to k T k k T T k i T P i k i k T k k i i i i T r r s B F

Constraint reaction forces in different coordinate system Ek Tk Constraint force vector and torque with respect to o-xy r Xj F=-,九 T=sPB,西2-Φ X Ek Tk Constraint force vector and torque with respect to body-fixed frame o-xiyi E"R=ATFR Tk =Tk
k T k k T T k i T P i k i k T k k i i i i T r r s B F k i k Fi , T Constraint force vector and torque with respect to o-xy k T k i i i k k Ti Ti F A F Constraint reaction forces in different coordinate system k i k Fi , T x y Constraint force vector and torque with respect to body-fixed frame o-xiyi xi yi
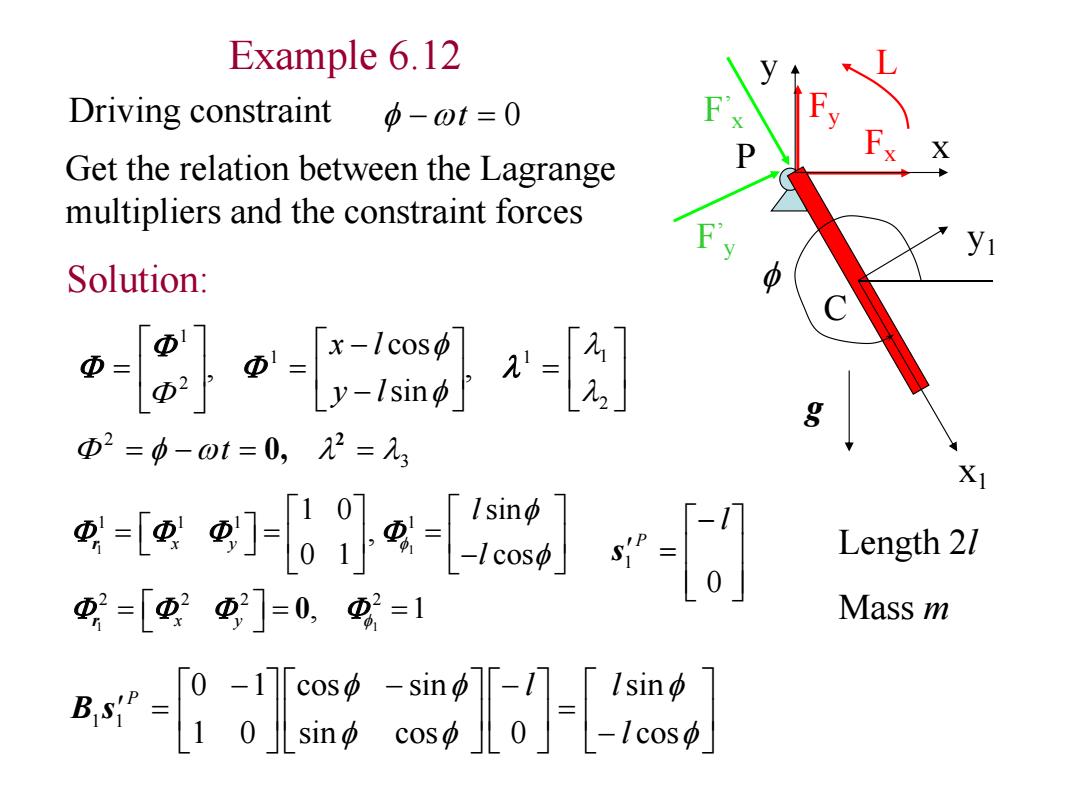
Example 6.12 Driving constraint 中-ot=0 Get the relation between the Lagrange multipliers and the constraint forces Solution: o-m- g Φ2=中-0t=0,2=元3 。ey-lgeg- Length 21 =[]=0,=1 Mass m g6-
Example 6.12 2 1 1 1 2 1 , sin cos , y l x l Fx F Fy ’x F’y L x1 y1 C x y g Length 2l Mass m P Driving constraint t 0 0 1 l P s 1 1 1 1 1 1 1 1 2 2 2 2 1 0 sin , 0 1 cos , 1 x y x y l l r r 0 cos sin sin cos 0 cos sin 1 0 0 1 1 1 l l l P B s 3 2 2 t 0, Solution: Get the relation between the Lagrange multipliers and the constraint forces
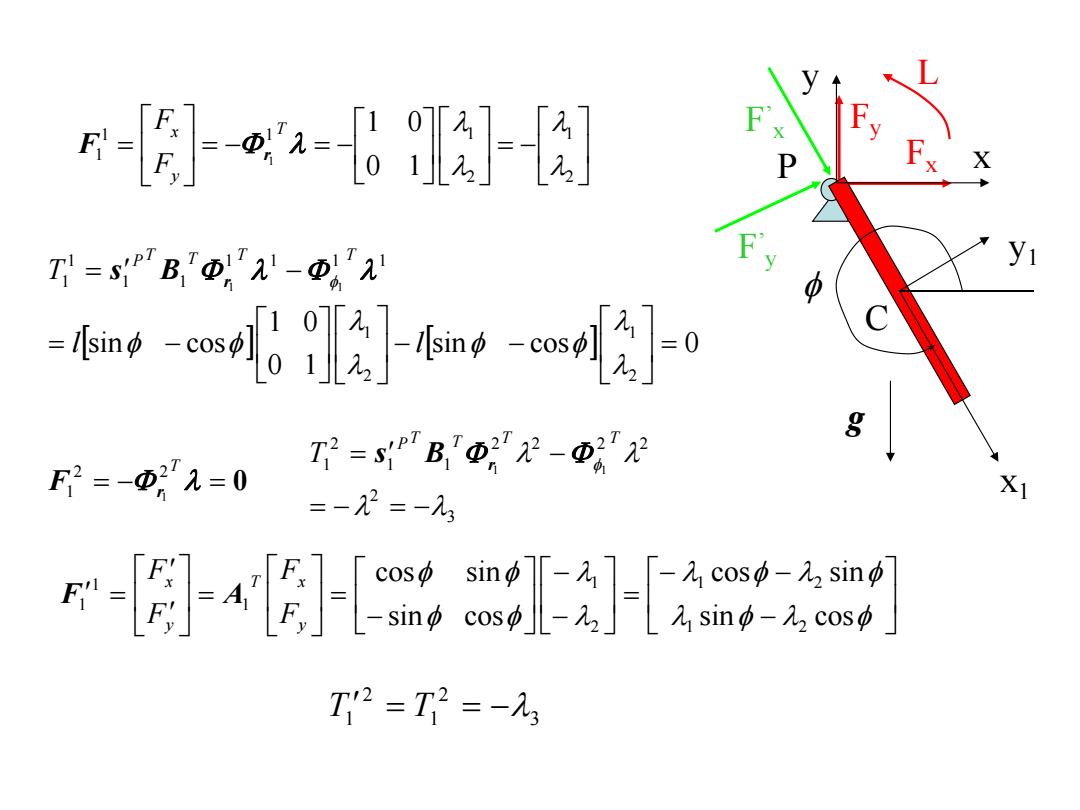
-。6-及 X T=sPB,'Φ,2-D -ew及知-o经]-0 F2=-2=0 T2=s"B =-22=-23 X1 r-卧[]-o T2=T2=-3
sin cos 0 0 1 1 0 sin cos 2 1 2 1 1 1 1 1 1 1 1 1 1 1 l l T T T T T P s B r 2 1 2 1 1 1 1 0 1 1 0 1 T y x F F F r Fx F Fy ’x F’y L x1 y1 C x y g P 0 T 2 2 1 1 F r 3 2 2 2 2 2 1 1 2 1 1 1 T T T T P T s B r sin cos cos sin sin cos cos sin 1 2 1 2 2 1 1 1 1 y T x y x F F F F F A 3 2 1 2 T1 T