上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.6-Position, velocity and acceleration analysis_1

3.6 Position,velocity and acceleration analysis Newton-Raphson algorithm D(q+4q,)=D(q,）+更（q,4q+high-order terms ≈(q,)+惠(q,)4g For(g+4g,）=0D(q,)+电(g,)4g=0 Iteration: 惠(q,）4g=-(q,）,k=1,… q+=q)+4q) Until4g≤&(&>0，e0，e<1)

3.6 Position, velocity and acceleration analysis Newton-Raphson algorithm           ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , , , , , k k k k k k k k t t t high order terms t t           q q q q q q q q q q      For   ( ) ( ) , k k  q  q t  0     ( ) ( ) ( ) , , k k k  q t q q t q  0     ( ) ( ) ( ) , , , 1, k k k q q t q   q t k   (k 1) (k ) (k )   q  q  q Until   ( ) 0, 1 k q       Iteration: or     ( 1) , 0, 1 k t      q   

Example 2.6.2 x -cos y-sin =1 x2 -coso -cos 1 B 2 Φ(q,)= y2-sind-sin 12=1 +1 5π —t- 中2 X2 6 3 1 0 sing 0 0 0 -c0s442 01 -c0s功 0 0 0 -sing 0 0 sing 1 0 sing -c0s442-cos44,2 更，(q,）= Y= 0 0 -cos 01 -C0s42 singo2-sin 0 0 0 01 0 0 0 0 1 0 0 0 0

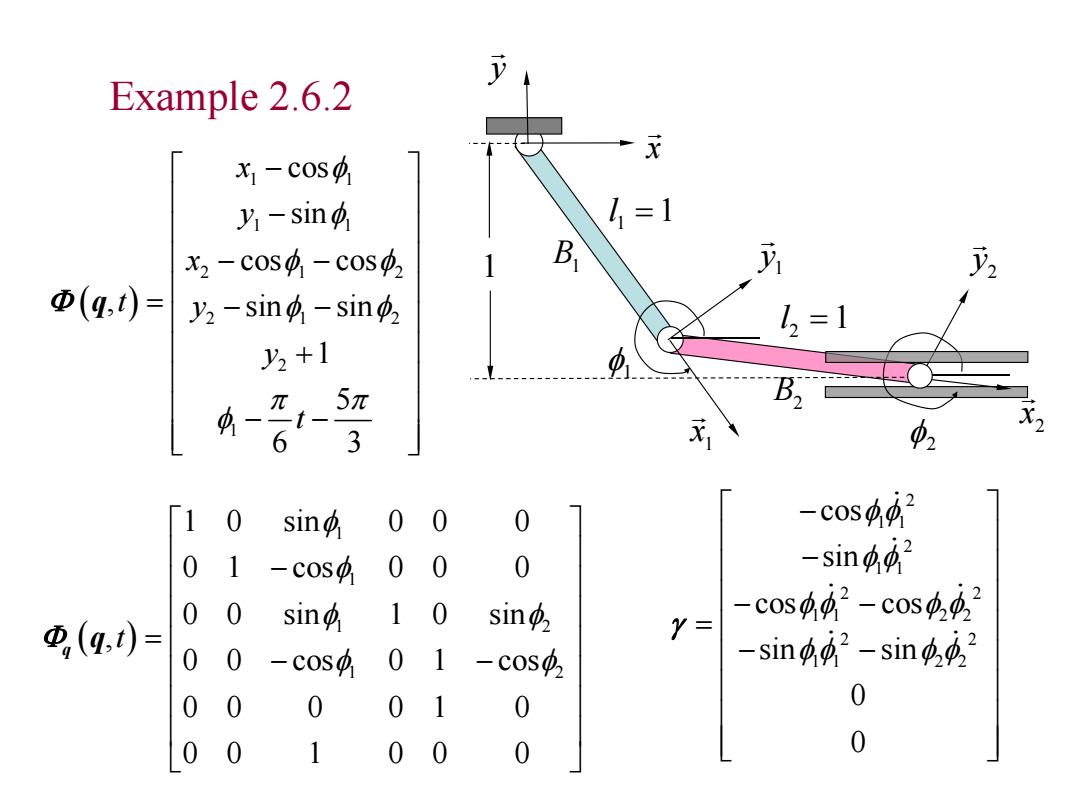
Example 2.6.2 1 x  1 y  2 x  2 y  x  y  1 2 1 1 l  1 2 l  1 B2 B1   1 1 1 1 2 1 2 2 1 2 2 1 cos sin cos cos , sin sin 1 5 6 3 x y x t y y t                           q   1 1 1 2 1 2 1 0 sin 0 0 0 0 1 cos 0 0 0 0 0 sin 1 0 sin , 0 0 cos 0 1 cos 0 0 0 0 1 0 0 0 1 0 0 0 t                 q  q 2 1 1 2 1 1 2 2 1 1 2 2 2 2 1 1 2 2 cos sin cos cos sin sin 0 0                                

Fort=0 功= 5π 3 x1-cos 0.5 y-sind -0.8660 x2-cos-cos 5m/3 Φ(4，)= y2-sind-sin Estimate 1.5 当+1 z1- π -1.0 63 6.14 1 0 sing 00 0 0 1 -cos 00 0 0 0 sing 1 0 更，(g,）)= sin 00 -cos 0 1 -c0s42 0 0 0 01 0 0 0 1 00 0 Sove电(g,0)4g=-Φ(g,0）

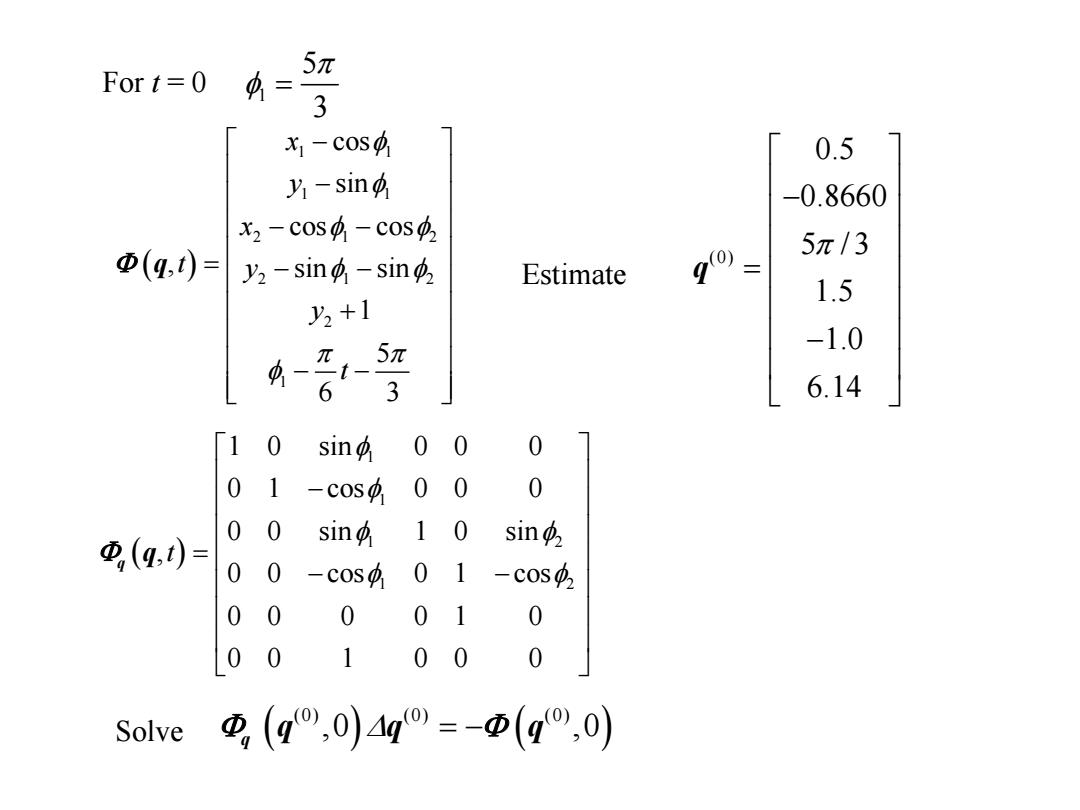
  1 1 1 1 2 1 2 2 1 2 2 1 cos sin cos cos , sin sin 1 5 6 3 x y x t y y t                           q Estimate For t = 0 1 5 3    (0) 0.5 0.8660 5 / 3 1.5 1.0 6.14           q   1 1 1 2 1 2 1 0 sin 0 0 0 0 1 cos 0 0 0 0 0 sin 1 0 sin , 0 0 cos 0 1 cos 0 0 0 0 1 0 0 0 1 0 0 0 t                 q  q Solve     (0) (0) (0) ,0    ,0 q  q q  q

x0=0.5y0=-0.866040)=5 π/3 x0=1.5y0=-1.040=6.14 1 0 sin) 00 0 x0)-c0s40) 01 -c0s40 0 0 0 4y0 yo)-sino) 0 0 sin) 1 0 sin x0-c0s40-c0s40 0 0 -c0s40) 0 1 -c0s40 yo)-sing)-sin) 0 0 0 0 1 0 +1 5π 0 0 1 0 0 0 40 3 0.5 0 -0.8660 0 5π/3 A -0.0089 1.4911 0 -1.0 4 0.0088 6.1488

(0) (0) (0) (0) 1 1 1 1 (0) (0) (0) (0) 1 1 1 1 (0) (0) (0) (0) (0) 2 1 1 2 1 (0) (0) (0) 1 2 2 (0) 2 (0) 2 cos 1 0 sin 0 0 0 sin 0 1 cos 0 0 0 cos 0 0 sin 1 0 sin 0 0 cos 0 1 cos 0 0 0 0 1 0 0 0 1 0 0 0 x x y y x x y                                                 (0) 2 (0) (0) (0) 2 1 2 (0) 2 (0) 1 cos sin sin 1 5 3 y y                (0) 1   5 / 3 (0) 2   6.14 (0) 1 x  0.5 (0) 1 y  0.8660 (0) 2 x  1.5 (0) 2 y  1.0 (0) 1 (0) 1 (0) 1 (0) 2 (0) 2 (0) 2 0 0 0 0.0089 0 0.0088 x y x y                     (1) (0) (0) 1 1 1 (1) (0) (0) 1 1 1 (1) (0) (0) 1 1 1 (1) (0) (0) 2 2 2 (1) (0) (0) 2 2 2 (1) (0) (0) 2 2 2 0.5 0.8660 5 / 3 1.4911 1.0 6.1488 x x x y y y x x x y y y                                                                                 

x0=0.5y0=-0.866040) = 5π/3x°=1.4911y0=-1.04=6.1488 1 0 sin 00 0 -cos 01 -c0s40 00 0 -sin) 0 0 sin 1 0 sin) x-cos)-cos) 0 0 0 1 y-sin-sin 0 0 0 0 1 0 +1 5π 0 0 1 0 0 0 40 3 0.5 0 -0.8660 0 5π/3 -0.0001 1.4910 0 -1.0 0 6.1488

(1) (1) (1) (1) 1 1 1 1 (1) (1) (1) (1) 1 1 1 1 (1) (1) (1) (1) (1) 2 1 1 2 1 (1) (1) (1) 1 2 2 (1) 2 (1) 2 cos 1 0 sin 0 0 0 sin 0 1 cos 0 0 0 cos 0 0 sin 1 0 sin 0 0 cos 0 1 cos 0 0 0 0 1 0 0 0 1 0 0 0 x x y y x x y                                                 (1) 2 (1) (1) (1) 2 1 2 (1) 2 (1) 1 cos sin sin 1 5 3 y y                (0) 1   5 / 3 (0) 2 (0)   6.1488 1 x  0.5 (0) 1 y  0.8660 (0) 2 x  1.4911 (0) 2 y  1.0 (1) 1 (1) 1 (1) 1 (1) 2 (1) 2 (1) 2 0 0 0 0.0001 0 0 x y x y                     (2) (1) (1) 1 1 1 (2) (1) (1) 1 1 1 (2) (1) (1) 1 1 1 (2) (1) (1) 2 2 2 (2) (1) (1) 2 2 2 (2) (1) (1) 2 2 2 0.5 0.8660 5 / 3 1.4910 1.0 6.1488 x x x y y y x x x y y y                                                                                 

0.5 -0.8660 0 4q0= 5π/3 -0.0001 q2)= 1.4910 0 -1.0 0 6.1488 8=0.0001 Since s=)is the generalized coordinate vector for0

(1) 1 (1) 1 (1) (1) 1 (1) 2 (1) 2 (1) 2 0 0 0 0.0001 0 0 x y x y                           q (2) (1) (1) 1 1 1 (2) (1) (1) 1 1 1 (2) (1) (1) (2) 1 1 1 (2) (1) (1) 2 2 2 (2) (1) (1) 2 2 2 (2) (1) (1) 2 2 2 0.5 0.8660 5 / 3 1.4910 1.0 6.1488 x x x y y y x x x y y y                                                                             q     Since (1) q   (2) q  q is the generalized coordinate vector for t = 0   0.0001

X 0.5 为 -0.8660 4 5π/3 9= X2 1.4910 -1.0 4, 6.1488 Solve velocity constraint equation 1 0 sin 0 0 0 0 0.4534 0 1 -cos 0 0 0 0 0.2618 0 0 sin 1 0 sin 西 0 0.5236 9= 0 0 -cos 01 -cos 2 0 元2 0.4180 0 0 0 01 0 0 2 0 0 0 1 00 0 π/6 -0.2642

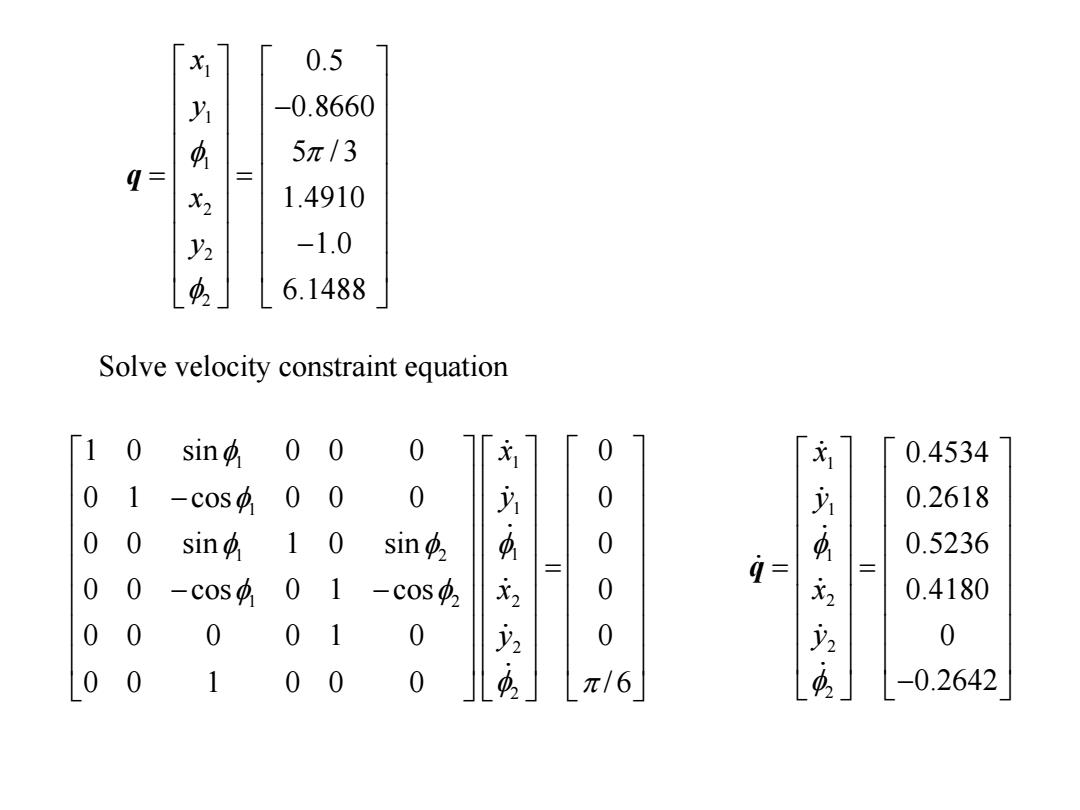
Solve velocity constraint equation 1 1 1 1 1 2 1 1 2 222 1 0 sin 0 0 0 0 0 1 cos 0 0 0 0 0 0 sin 1 0 sin 0 0 0 cos 0 1 cos 0 0 0 0 0 1 0 0 0 0 1 0 0 0 / 6 xyxy                                                                    111222 0.5 0.8660 5 / 3 1.4910 1.0 6.1488 xyxy                       q 111222 0.4534 0.2618 0.5236 0.4180 0 0.2642 xyxy                    q   

1 0.4534 -c0s442 y 0.2618 singo2 中 0.5236 -c0s42-cos44,2 9= Y= 元2 0.4180 -singo2-sin 0 0 -0.2642 0 Solve acceleration constraint equation 1 0 sin 0 0 0 1 -c0s442 -0.1371 0 1 -cos 0 0 0 -sing2 0.2374 0 0 sing 1 0 sin 西 -c0s442-c0s4,4,2 或 -0.2063 i= 0 0 -cos 01 -c0s42 元2 -sing2-sinp,项，2 -0.2468 0 0 0 0 1 0 0 0 0 0 1 00 0 0

Solve acceleration constraint equation 2 1 1 1 1 2 1 1 1 1 2 2 1 2 1 1 1 2 2 2 2 1 2 2 1 1 2 2 2 2 1 0 sin 0 0 0 cos 0 1 cos 0 0 0 sin 0 0 sin 1 0 sin cos cos 0 0 cos 0 1 cos sin sin 0 0 0 0 1 0 0 0 0 1 0 0 0 0 x y x y                                                                        1 1 1 2 2 2 0.4534 0.2618 0.5236 0.4180 0 0.2642 x y x y                     q        2 1 1 2 1 1 2 2 1 1 2 2 2 2 1 1 2 2 cos sin cos cos sin sin 0 0                                 1 1 1 2 2 2 0.1371 0.2374 0.2063 0.2468 0 0 x y x y                       q       