
6.3 Equations of motion of constrained planar systems 6.3.1 Variational equations of motion for planar systems ∑δ[M,i-g]=0> δq[M-]=0 Composite state variable vector g=h…g Composite mass matrix M=diag(M,.M) Composite veetor of generalized forces
6.3 Equations of motion of constrained planar systems 6.3.1 Variational equations of motion for planar systems Composite state variable vector T T nb T q q1 q diag( , ) C M M1 Mnb omposite mass matrix Composite vector of generalized forces T T nb T Q Q1 Q 0 nb i i i i T i 1 q M q Q q Mq Q 0 T

The form of constrained variational equations FA,n Applied force and torque, including all forces acting on or between bodies except forces and torques of constraint Fc.nc Constraint force and torque ,2,29 2 Generalized applied force 2 Generalized constraint force 2=2,+2
A Fi A ni C Fi C ni The form of constrained variational equations C i A Qi Qi Q A i A i F , n Applied force and torque, including all forces acting on or between bodies except forces and torques of constraint Constraint force and torque C i C i F , n C i A Qi , Q A Qi Generalized applied force C Qi Generalized constraint force

The form of constrained variational equations The variational equations of motion ∑mMi,-g]∑me=0 If attention is restricted to virtual displacements that are consistent with the constraints that act on the system (without friction) ∑42,=0 i= 0 2ogMg.-2l=0>6g-2l-0 g=a…g7M=diag(M,…M)Q=27…2
The variational equations of motion 0 1 1 nb i C i T i nb i A i i T qi Mq Q q Q If attention is restricted to virtual displacements that are consistent with the constraints that act on the system (without friction) 0 1 nb i C i T qi Q 0 1 nb i A i i T qi Mq Q 0 T A q Mq Q T T nb T q q1 q diag( , ) M M1 Mnb T T A nb T A A Q Q1 Q The form of constrained variational equations

The form of constrained variational equations For all virtual displacements &g that are consistent with constraints that act on the system,the constraint variational equations of motion are δq[Mi-0]=0 The combined set of kinematic and driving constraints is Φ(q,t)=0 >中,8q=0 ∫δqMi-g]=0 for &g that are consistent Φ,δq=0 with constraints A Mi-04=0 Why
0 T A q Mq Q The form of constrained variational equations (q,t) 0 q 0 q For all virtual displacements q that are consistent with constraints that act on the system, the constraint variational equations of motion are The combined set of kinematic and driving constraints is q 0 q Mq Q q 0 T A for q that are consistent with constraints 0 A Mq Q Why ?

6.3.2 Lagrange Multiplier Let b be an n vector of constants,x be an n vector of variables, and A be an mXn constant matrix If bx=0 holds for all x that satisfy x=0 There exists an m vectorA of Lagrange Multiplier such that bx+Ax=x"(b+)=0 for arbitrary x b+AT元=0 Since Mi-Q4δq=0 holds for all6 that satisfy中,δq=0 There exists an m vector of Lagrange Multiplier such that M-2δg+2'Φ,6q=6g(Mi-g+Φ,2)=0 for arbitraryδq >Mi-2+Φ2=0 Why
6.3.2 Lagrange Multiplier There exists an m vector l of Lagrange Multiplier such that Let b be an n vector of constants, x be an n vector of variables, and A be an m×n constant matrix b x 0 T If holds for all x that satisfy Ax 0 l ( l) 0 T T T T b x Ax x b A for arbitrary x Mq Q q 0 T A q 0 Since holds for all q that satisfy q There exists an m vector l of Lagrange Multiplier such that l l 0 T T A T T A q Q q Mq Q q q q Mq for arbitrary q l 0 A T Q q Mq Why ? l 0 T b A

6.3.3 Mixed differential-algebraic equations of motion There exists an m vectorA of Lagrange Multiplier such that δq(Mi-2+p,2)=0 for arbitraryδq Therefore,the coefficient of g must be zero,yielding the Lagrange multiplier form of equations Mi+D,2=24 Recall the velocity and acceleration equations 中1=-更,=v,中,i=-(Φ,),i-2Φ9i-D1=Y Mixed differential-algebraic equations of motion 2-9
6.3.3 Mixed differential-algebraic equations of motion There exists an m vector l of Lagrange Multiplier such that l 0 T A T Q q q Mq for arbitrary q Therefore, the coefficient of q must be zero , yielding the Lagrange multiplier form of equations T A Mq q l Q Recall the velocity and acceleration equations t t tt q v q q q q q q q q q , ( ) 2 l T A M q Q q q Mixed differential-algebraic equations of motion
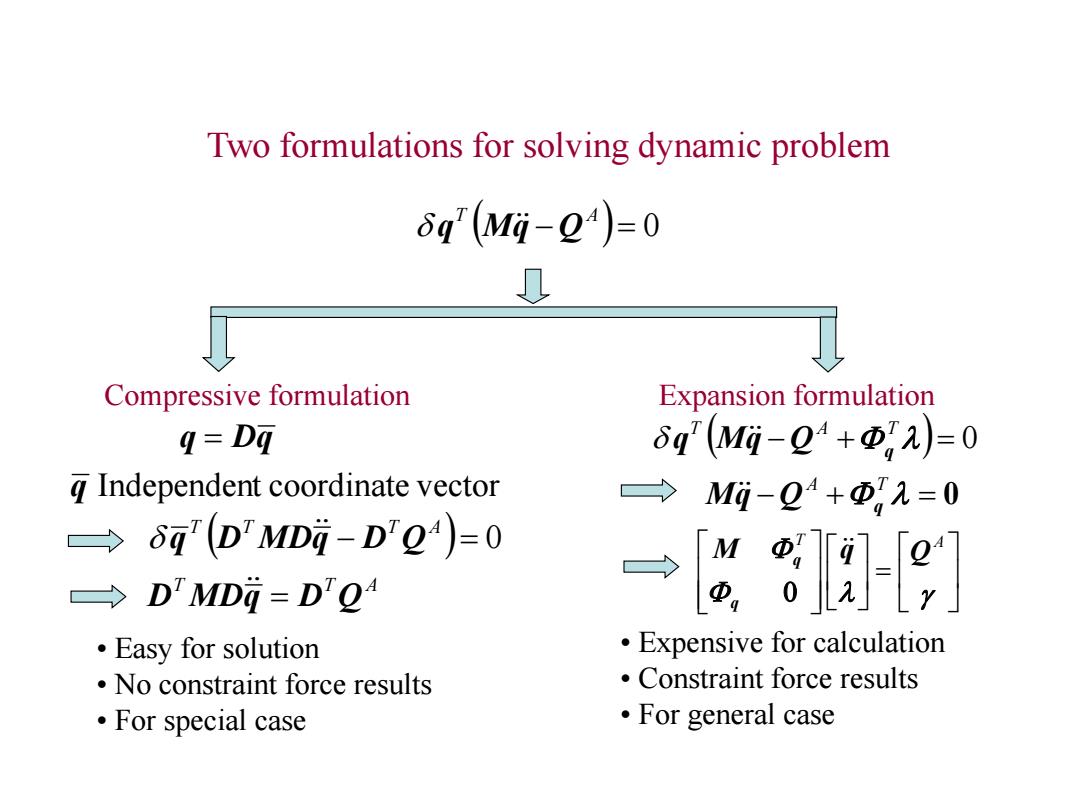
Two formulations for solving dynamic problem δg(M-Q4)=0 0 Compressive formulation Expansion formulation q=Dq 6q(Mi-2+Φ,2=0 g Independent coordinate vector →Mi-2+Φ,2=0 →δ7(D'MDi-D2)=0 D'MDG-D'Q →&8-e] ·Easy for solution Expensive for calculation No constraint force results Constraint force results ·For special case ·For general case
Two formulations for solving dynamic problem 0 T A q Mq Q q Dq 0 T T T A q D MDq D Q q Independent coordinate vector T T A D MDq D Q • Easy for solution • No constraint force results • For special case Compressive formulation Expansion formulation l 0 T A T Q q q Mq l 0 A T Q q Mq l T A M q Q q q • Expensive for calculation • Constraint force results • For general case

Constraint dynamic existence theorem Condition (I)Φ,has full row rank (2)dMod>0 for any nonzero virtual velocity that is consistent with the constraint Result For allδi≠0 is nonsingular ,A are uniquely determined Failure (1)Singular configurafiares (2)System with redundant joints (3)M is not positive,that is,some of the diagonal elements vanish
Constraint dynamic existence theorem q (1) has full row rank Condition For all q 0 is nonsingular q M q T q, l are uniquely determined (1) Singular configuration (2) System with redundant joints (3) M is not positive, that is, some of the diagonal elements vanish q M q 0 T (2) for any nonzero virtual velocity that is consistent with the constraint Result Failure cases

Initial position condition System constraint equations involve both kinematic and driving constraint of the form g-08 Initial position conditions are defined in the form ow-- Which is required that (1)The number of the equations be equal to the number of system degrees of freedom (2)(g(t),t)=0 must be independent to uniquely determine g(to)
Initial position condition ( , ) ( ) ( , ) t t D K q q q Initial position conditions are defined in the form 0 ( ( ), ) ( ( )) ( ( ), ) 0 0 0 0 0 t t t t t D K l q q q Which is required that (1) The number of the equations be equal to the number of system degrees of freedom (2) must be independent to uniquely determine q (t0 ( ( ), ) 0 ) 0 0 t t l q System constraint equations involve both kinematic and driving constraint of the form

Initial velocity condition System constraint Jacobian Initial position conditions are defined in the form Φ,(to)i(t)=v(to) Which is required that (1)The number of the equations be equal to the number of system degrees of freedom (2)()()=v(t)must be independent to uniquely determine a(t)
Which is required that (1) The number of the equations be equal to the number of system degrees of freedom (2) (t0 ) (t0 ) (t0 ) must be independent to uniquely determine l q v q ( )0 q t Initial velocity condition D K q q q Initial position conditions are defined in the form ( ) ( ) ( ) 0 0 0 t t t l q v q System constraint Jacobian