上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_动力学上机_双摆动力学仿真说明

Dynamic Analysis of Double Pendulum 2 B2 Link BI is connected to the ground with revolute joint O,connect to B2 with revolute joint 4. Given parameters: m1=m2=m,1=l2=1,m=1kg,1=1m Initial condition 4(0)=0,4,(0)=0,,(0)=0,p2(0)=0 go-日0000,9o-p0000o Calculate time histories ofRR Constraint equation 1 xcos y Φ= ysin 中 ，0= X2 2c0s0-x- 2 cosd X2 片-2sin4-y-2sin4 2 Jacobian and right side of acceleration equation

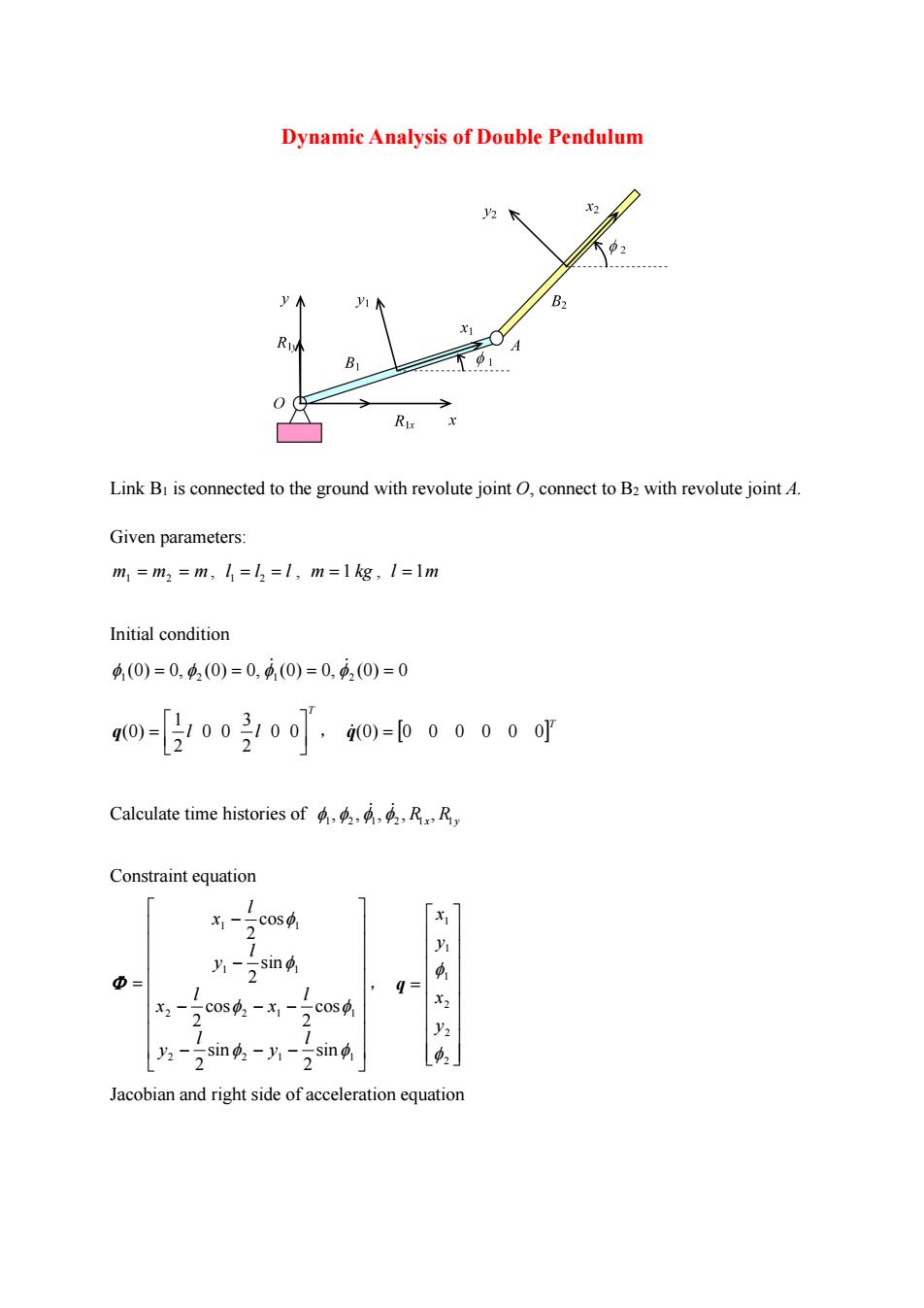
Dynamic Analysis of Double Pendulum Link B1 is connected to the ground with revolute joint O, connect to B2 with revolute joint A. Given parameters: m1  m2  m , 1 2 l  l  l , m  1 kg , l  1m Initial condition (0) 0, (0) 0, (0) 0, (0) 0 1   2  1   2    T l l        0 0 2 3 0 0 2 1 q(0) ，   T q(0)  0 0 0 0 0 0 Calculate time histories of 1 2 1 2 1 1 , , , , ,     R x R y   Constraint equation                2 2 1 1 2 2 1 1 1 1 1 1 sin 2 sin 2 cos 2 cos 2 sin 2 cos 2       l y l y l x l x l y l x  ，      2 2 2 1 1 1   y x y x q Jacobian and right side of acceleration equation

10sim4000 -2c0s4 21 01-cos4,00 2sin4 ,= y= 2 -10 sin 1 0 2 2c0s4- 2 2 0-1-2c0s401-2cos4 Solve &]图- m 0 m -mg ml2/12 M= Q1= 0 心 mg ml2/12 0 Rx=-,R,=-九2 For each time step,solve AX=B 4gx[[图- 头 丐 Let y=q= 3=9= 元2 y 乌 Differential equation: Initial condition y(0)] 4(0) ,0 (0)

            1 2 1 2 1 1 cos 2 cos 0 1 2 0 1 sin 2 sin 1 0 2 1 0 cos 0 0 0 2 0 1 sin 0 0 0 2 1 0       l l l l l l  q ，              2 2 1 2 2 1 2 2 1 2 2 1 1 2 1 1 2 1 sin 2 sin 2 cos 2 cos 2 sin 2 cos 2                   l l l l l l  Solve                     T A M q Q q q  0      /12 /12 2 2 ml m m ml m m M ，       0 0 0 0 mg mg A Q 1 1 1 2 , R x   R y   For each time step, solve A X  B 1 2 , , T A                             q q M X q Q A X B X  0     Let 1 1 1 1 2 2 2 x y x y           y q , 1 1 1 2 2 2 2 x y x y           y q        Differential equation:             1 2 2 1 X y y y   Initial condition             (0) (0) (0) (0) 2 1 q q y y 

Flow chart 开始00 9=90, 9=4o 计算A= M B= Lx] 0 是 A奇异 > 香 解方程AX=B,得到X=XIX, 令s=4,r=9 对方程 5=r, s(to)=90 积分一次 r=X1, r(to)=90 ↓ 1=1。+41,q=s(),9=r(t),违约校正 0-t 90=9 90=9 [Imax 是 否 结

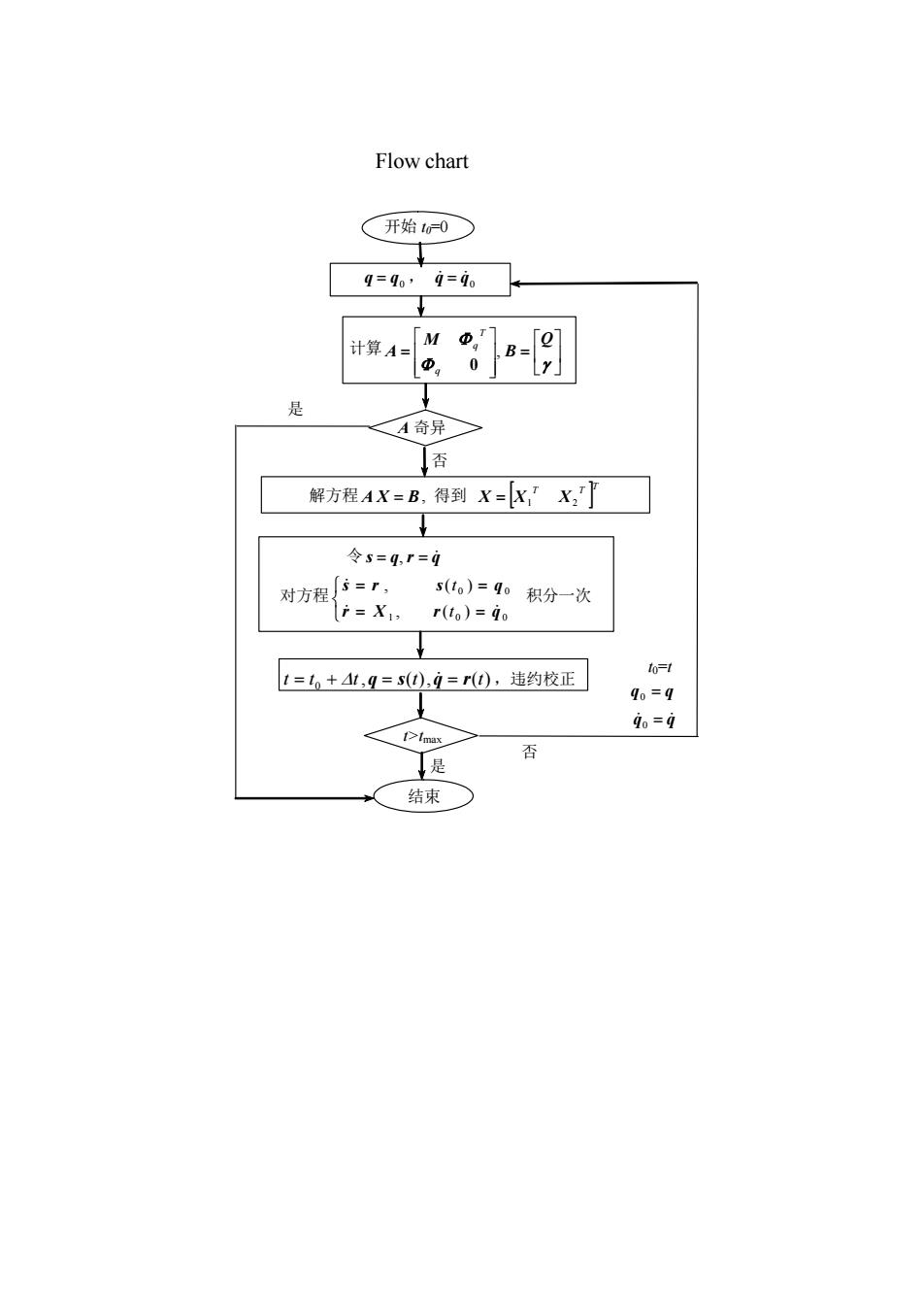
Flow chart 开始 t0=0 0 q  q ， 0 q  q 计算                Q B M A , 0 q T q 解方程 A X  B, 得到   T T T X  X1 X2 是 结束 对方程        1 0 0 0 0 , ( ) , ( ) r X r q s r s q    t t 积分一次 令 s  q, r  q , ( ), ( ) 0 t  t  t q  s t q  r t ，违约校正 是 否 q  q 0 t0=t A 奇异 t>tmax 否 q  q 0