上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 7_chap7-Numerical Methods in Dynamics

Chapter 7 Numerical Methods in Dynamics 7.1 Organization of Computations Dynamics computational flow 。Preprocessor Dynamic Analysis Program 。Postprocessor

Chapter 7 Numerical Methods in Dynamics Dynamics computational flow l Preprocessor l Dynamic Analysis Program l Postprocessor 7.1 Organization of Computations

Preprocessor 。Enter kinematic data Enter body inertia data Enter applied force data Enter spring-damper-actuator data Enter initial condition ·Define analysis mode (Equilibrium,dynamic,inverse dynamic) Define output desired

• Enter kinematic data • Enter body inertia data • Enter applied force data • Enter spring-damper-actuator data • Enter initial condition • Define analysis mode (Equilibrium, dynamic, inverse dynamic) • Define output desired Preprocessor

Dynamic analysis program Construct equations and matrices for dynamic analysis Assemble system or declare infeasible design Identify and eliminate redundant constraints Carry out equilibrium,dynamic and inverse dynamic analysis

Dynamic analysis program • Construct equations and matrices for dynamic analysis • Assemble system or declare infeasible design • Identify and eliminate redundant constraints • Carry out equilibrium, dynamic and inverse dynamic analysis

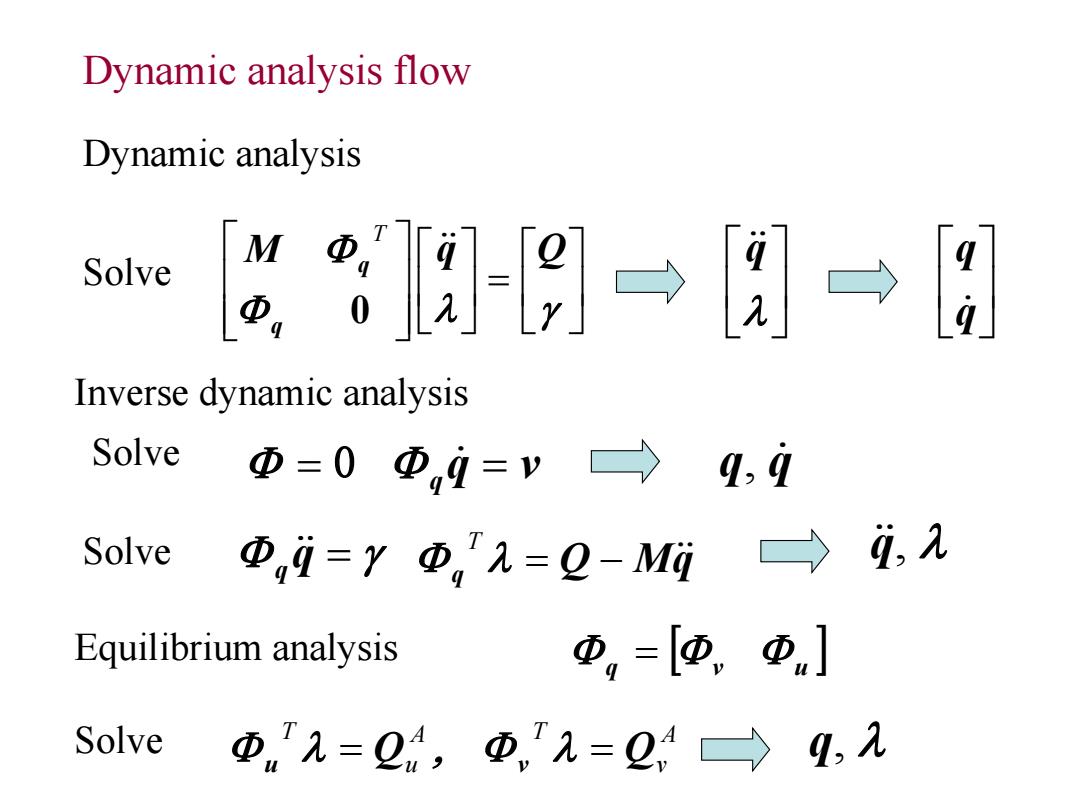
Dynamic analysis flow Dynamic analysis Solve 9→ Φg 牙 → Inverse dynamic analysis Solve Φ=0Φi=v→ q,9 Solve ΦD,i=YΦ，'九=2-Mi 〉 i,2 Equilibrium analysis Φ，=[匝，中] Solve Φ元=2，Φ，1=2，之q,九

Dynamic analysis flow Dynamic analysis Solve                    M  q Q q q  0 T        q       q q  Inverse dynamic analysis Solve  q   q  Q Mq q      T q,  Solve q v   0  q   q, q Equilibrium analysis    q   v  u A v A T u T Solve  u   Q   v   Q q, 

Postprocessor Print alphanumeric results ·Plot curves Transmit graphic animation to terminal screen/ video tape

Postprocessor • Print alphanumeric results • Plot curves • Transmit graphic animation to terminal screen / video tape

7.2 Mixed differential-algebraic equations M Dynamic equations 9 Kinematic constraint equations Φ(q)=0Φ，9=v Comprise the mixed differential-algebraic equations of motion

7.2 Mixed differential-algebraic equations Dynamic equations                    M  q Q q q  0 T Kinematic constraint equations (q)  0 q v  q   Comprise the mixed differential-algebraic equations of motion

7.3 Proposed solution methods for Mixed differential- algebraic equations 1.Coordinates partitioning v:Independent coordinates g= u:coordinates dependent on v u=f(v) 功，=[ Φ] Φ4=V Φ，i=Y Φi+Φ=VΦi+Φ，i=Y In case that is nonsingular i=Φw(V-Φ) i=Φ(y-更)

7.3 Proposed solution methods for Mixed differential- algebraic equations        v u q u  q   u  v   qq V  q   q   uu  v v V  u  v   u v   ( ) 1 u V v u v      ( ) 1 u v u v       u  f (v)

We can write M+Φ，=24 M as 如百®-8 (1) M Substitute i=Φn(y-Φ into equation (1) and eliminate M节=9 Where i=M"-M“D..-,7画.Y(M"-M"电.'，） 2=g-M"更.y-更西yg-Mm中.y）

( ) 1 u v u v       T A Mq q   Q                          Av Au T T vu vv uu uv Q Q v u M M M M v u      M ˆ v Q ˆ       M M M  u  v  v  u M M  u  v 1 1 1 ˆ        uv uu T vv vu T          1 1 1 ˆ    Q  Q  M u  v u Q  M u Au uu T Av vu T

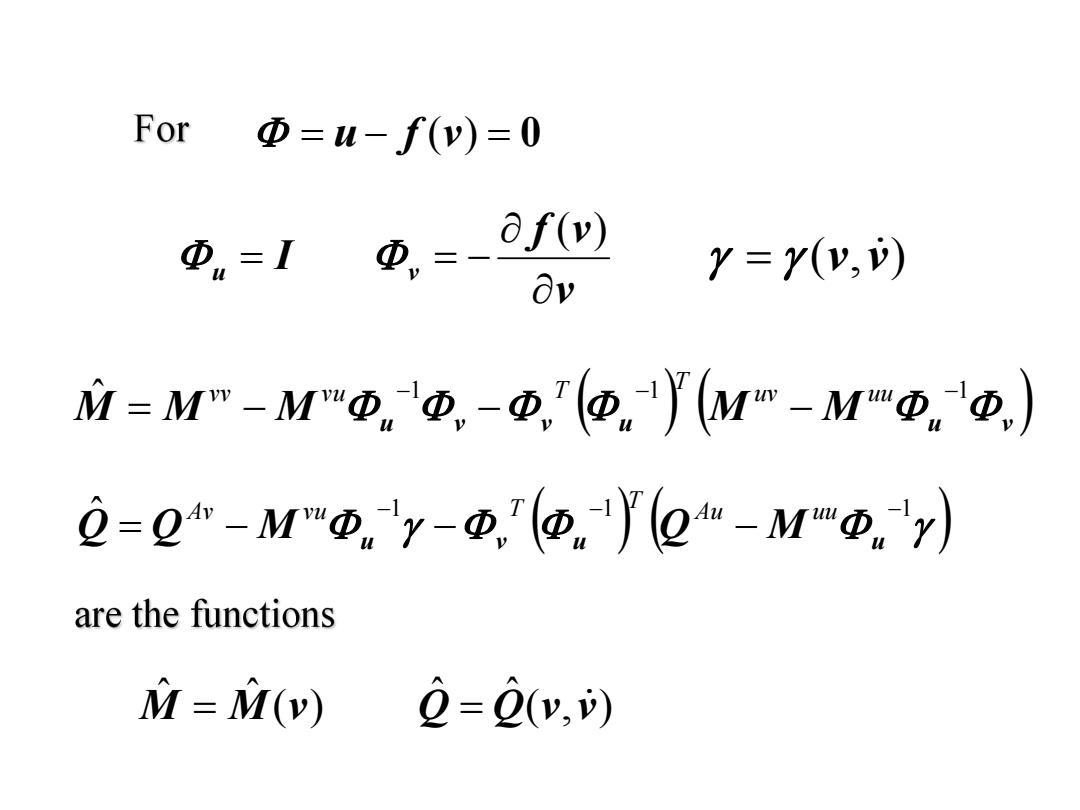
For Φ=u-f(v)=0 D=1D= of(v) Y=Y(v,v) Ov =M"-MmD.更，-更，西，y(Mm-M中.'o） ⑨=0-M更，y-更，西.y但-MΦy） are the functions M=M(v) 0=0(,)

  u  f (v)  0 I  u      M M M  u  v  v  u M M  u  v 1 1 1 ˆ        uv uu T vv vu T          1 1 1 ˆ    Q  Q  M u  v u Q  M u Au uu T Av vu T v f v v     ( )  ( ) ˆ ˆ M  M v ( , ) ˆ ˆ Q  Q v v    (v,v)

Step 1: For t=0v(0),(0) are given Solve u(0)=f(v(0) a(0)=af(0)0) 〉 (0),(0) Step 2: Solve M节=Q i =M-Q Step 3: Let S=V,P=少 5=r,r=M0 Integrate for one time step s(to)=v(to),r(to)=v(to)

( ) ( ), ( ) ( ) ˆ ˆ , 0 0 0 0 1 s t v t r t v t s r r M Q         M ˆ v Q ˆ   v Mˆ 1Qˆ   s v,r v 0 t0  v(0), v(0) u(0)  f (v (0)) (0) (0) ( ) (0) v v f v u     u(0), u(0)