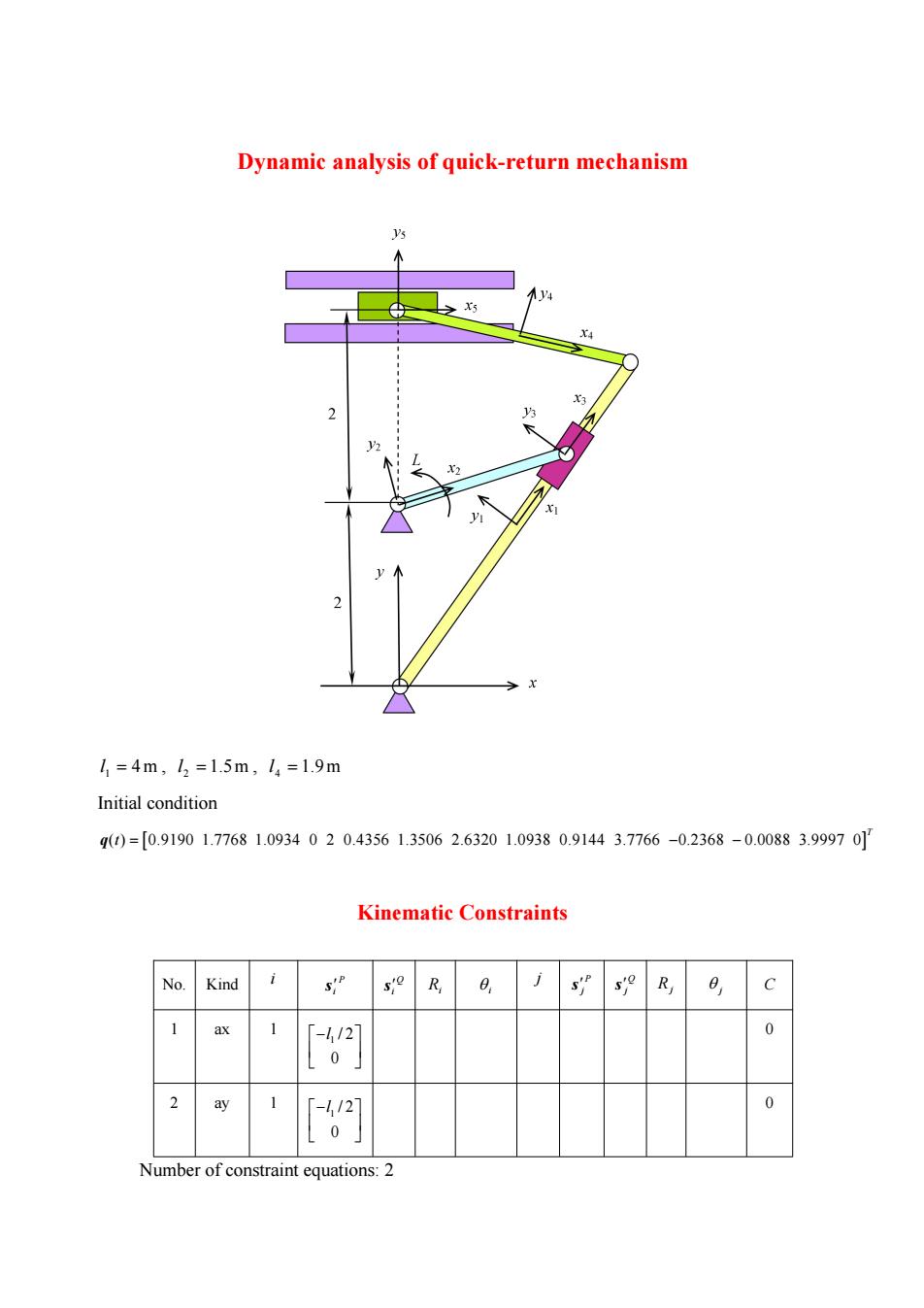
Dynamic analysis of quick-return mechanism 小4 >X5 X3 V2 X2 1=4m,12=1.5m,14=1.9m Initial condition q()=[0.91901.77681.0934020.43561.35062.63201.09380.91443.7766-0.2368-0.00883.99970 Kinematic Constraints No. Kind o R 0 s so R, C 1 ax 1 -4/2 0 ay 12 0 0」 Number of constraint equations:2
Dynamic analysis of quick-return mechanism l1 4m , l2 1.5m , l4 1.9m Initial condition ( ) 0.9190 1.7768 1.0934 0 2 0.4356 1.3506 2.6320 1.0938 0.9144 3.7766 0.2368 0.0088 3.9997 0 T q t Kinematic Constraints No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C 1 ax 1 1 / 2 0 l 0 2 ay 1 1 / 2 0 l 0 Number of constraint equations: 2

os 2 Φ0=y- sin No. Kind i SiP 59 R j R 3 ax v [8 0 4 ay 2 2 o Number of constraint equations:2 Φ2)=X2, Φ2)=y2-2 No. Kind o R 0, j s s R, 0 C 5 2 3 o Number of constraint equations:2 (2,3) -[ c0s4,- sin; No. Kind sip sio 父 0, j s 。 &) 8 6 1 8 8 Number of constraint equations:2 - 中-4
(1) 1 1 1 cos 2 ax l x , (1) 1 1 1 sin 2 ay l y No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C 3 ax 2 0 0 0 4 ay 2 0 0 2 Number of constraint equations: 2 ( 2 ) 2 ax x , (2) 2 2 ay y No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C 5 r 2 20 l 3 0 0 Number of constraint equations: 2 ( 2,3) 3 2 2 2 2 3 2 2 2 cos sin sin cos 0 r x x l y y No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C 6 t 1 0 0 1 0 3 0 0 1 0 Number of constraint equations: 2 (1,3) 1 3 1 1 3 1 3 1 sin cos t x x y y

No. Kind s"o R 59 R C 7 4 0 0 Number of constraint equations:2 Φ1,4) cosφ4 sinφ4 2-[ sin No. Kind i s 59 R 0, s9 R, 8 C -112 J Ce Number of constraint equations:2 (45) [-[- cos sin 厂2] -sin No. Kind siP 。 0 j 59 R 8 C 9 ay 5 [8 4 10 a 5 0 Number of constraint equations:2 Φ5)=y5-4, Φ5)=4
No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C 7 r 1 1 / 2 0 l 4 4 / 2 0 l Number of constraint equations: 2 (1,4 ) 4 4 4 4 1 1 1 1 4 4 4 1 1 1 cos sin / 2 cos sin / 2 sin cos 0 sin cos 0 r x l x l y y No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C 8 r 4 4 / 2 0 l 5 0 0 Number of constraint equations: 2 ( 4,5) 5 4 4 4 4 5 4 4 4 cos sin / 2 sin cos 0 r x x l y y No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C 9 ay 5 0 0 4 10 a 5 0 Number of constraint equations: 2 (5) 5 4 ay y , (5) 5 a

Driving Constraints No. Kind s siQ R 0, s R C() 12 aod 2 ot+0.44 Φd0=4,-0.44-01 The Jacobian matrix 1 0 I sin/2 00 0 0 0000 0 000 0 1 -1cos4/200 0 0 0000 0 000 0 0 0 10 0 0 0000 0 000 0 0 0 01 0 0 0000 0 000 0 0 0 -10l2sin42 0000 0 000 0 0 0 0-1-2c0s42 0 1000 0 000 sing-cos a 00 0 -sing cos 00 0 0 000 0,= 0 0 -1 00 0 00100 0 000 -1 0 I sin/2 00 0 0 0010-1,si吨/2000 0 -1 -41cos4/200 0 0 00011cos4/2000 0 0 0 00 0 0 00-10-l4sip/2100 0 0 0 00 0 0 000-114c04/2010 0 0 0 00 0 0 0000 0 010 0 0 0 00 0 0 0000 0 001 0 0 0 00 1 0 0000 0 000 a=-sind(y;-y)-cos (x3-x)
Driving Constraints No. Kind i P i s Q i s Ri i j P j s Q j s Rj j C(t) 12 ad 2 t+0.44 (1) 2 0.44 a d t The Jacobian matrix 1 1 1 1 2 2 2 2 1 1 1 1 1 1 4 1 0 sin / 2 0 0 0 0 0 0 0 0 0 0 0 0 0 1 cos / 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 sin 1 0 0 0 0 0 0 0 0 0 0 0 0 1 cos 0 1 0 0 0 0 0 0 0 sin cos 0 0 0 sin cos 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 sin / 2 0 0 0 0 0 0 1 0 sin l l l l a l l q 4 1 1 4 4 4 4 4 4 / 2 0 0 0 0 1 cos / 2 0 0 0 0 0 0 0 1 cos / 2 0 0 0 0 0 0 0 0 0 0 0 0 1 0 sin / 2 1 0 0 0 0 0 0 0 0 0 0 0 0 1 cos / 2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 l l l l sin ( ) cos ( ) 1 3 1 1 3 1 a y y x x

-1cos442/2 0000000 -1sin4i2/2 0 0 -人c0s442 -4sin%42 2sin4(y3-)4+2c0s4(年-元)4+cos4(%-片)42-sin4(x-x)42 y= 0 Y= 0 -1c0s42/2+14cos项画2/2 0000000 -1sin442/2+l4sin项画2/2 14c0s项项,2/2 1,sin4域2/2 0 00
0 0 0 0 0 0 0 0 0 0 0 0 0 0 v , 2 1 1 1 2 1 1 1 2 2 2 2 2 2 2 2 2 2 1 3 1 1 1 3 1 1 1 3 1 1 1 3 1 1 2 2 1 1 1 4 4 4 2 2 1 1 1 4 4 4 2 4 4 4 4 cos / 2 sin / 2 0 0 cos sin 2sin ( ) 2cos ( ) cos ( ) sin ( ) 0 cos / 2 cos / 2 sin / 2 sin / 2 cos / 2 s l l l l y y x x y y x x l l l l l l 2 4 4 in / 2 0 0 0