上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.1-Basic Concepts

Chap.3 Planar Cartesian Kinematics 3.1 Basic Concepts in Planar Kinematics Body-fixed reference frame:A reference frame that is attached to and moves with the body Rigid body:If movement associated with deformation is small,compared with the overall movement of a body, then the body is considered as a rigid body Mechanism:A collection of rigid bodies that are arranged to allow relative motion Kinematics:The study of position,velocity and acceleration of a system of interconnected bodies that make up a mechanism

3.1 Basic Concepts in Planar Kinematics Body-fixed reference frame: A reference frame that is attached to and moves with the body Rigid body: If movement associated with deformation is small, compared with the overall movement of a body, then the body is considered as a rigid body Mechanism: A collection of rigid bodies that are arranged to allow relative motion Kinematics: The study of position, velocity and acceleration of a system of interconnected bodies that make up a mechanism Chap. 3 Planar Cartesian Kinematics

Kinematic analysis:The process of predicting position, velocity and acceleration once a design is specified A set of generalized coordinates:A set of variables that uniquely specifies the position and orientation of all bodies in a mechanism (the configuration of a rigid body) q=[4g2…9c]7 The vector of planar Cartesian generalized coordinates of body i: 4,=[飞，y]

Kinematic analysis: The process of predicting position, velocity and acceleration once a design is specified A set of generalized coordinates: A set of variables that uniquely specifies the position and orientation of all bodies in a mechanism (the configuration of a rigid body)   T q  q1 q2  qnc The vector of planar Cartesian generalized coordinates of body i:   T i i i i q  x y 

If a planar mechanism is made of nb rigid bodies,the number of planar Cartesian generalized coordinates is nc 3nb The vector of planar Cartesian generalized coordinates of the system: 9=la9.'…467] Holonomic kinematic constraint equation *(q,) Φ(q,t)=: =0 The constraint equations must imply the geometry of the joint

If a planar mechanism is made of nb rigid bodies, the number of planar Cartesian generalized coordinates is nc = 3nb   T T nb T T q  q1 q2  q Holonomic kinematic constraint equation The vector of planar Cartesian generalized coordinates of the system:  0        ( , ) ( , ) ( , ) 1 t t t k nh k k q q q     The constraint equations must imply the geometry of the joint

If the constraint equations are independent,the system is said to have nc-nh degrees of freedom DOF nc-nh=3xnb-nh If DOF independent driving constraints are specified for kinematic analysis ΦP(g,t)=0 Then,the configuration of the system can be determined by solving the constraint equations: mwy-l8ad-t Such a system is called kinematically driven

If the constraint equations are independent, the system is said to have nc – nh degrees of freedom Then, the configuration of the system can be determined by solving the constraint equations: If DOF independent driving constraints are specified for kinematic analysis   0       ( , ) ( , ) ( , ) t t t D k q q q    DOF  nc  nh  3 nb  nh ( ,t)  0 D  q Such a system is called kinematically driven

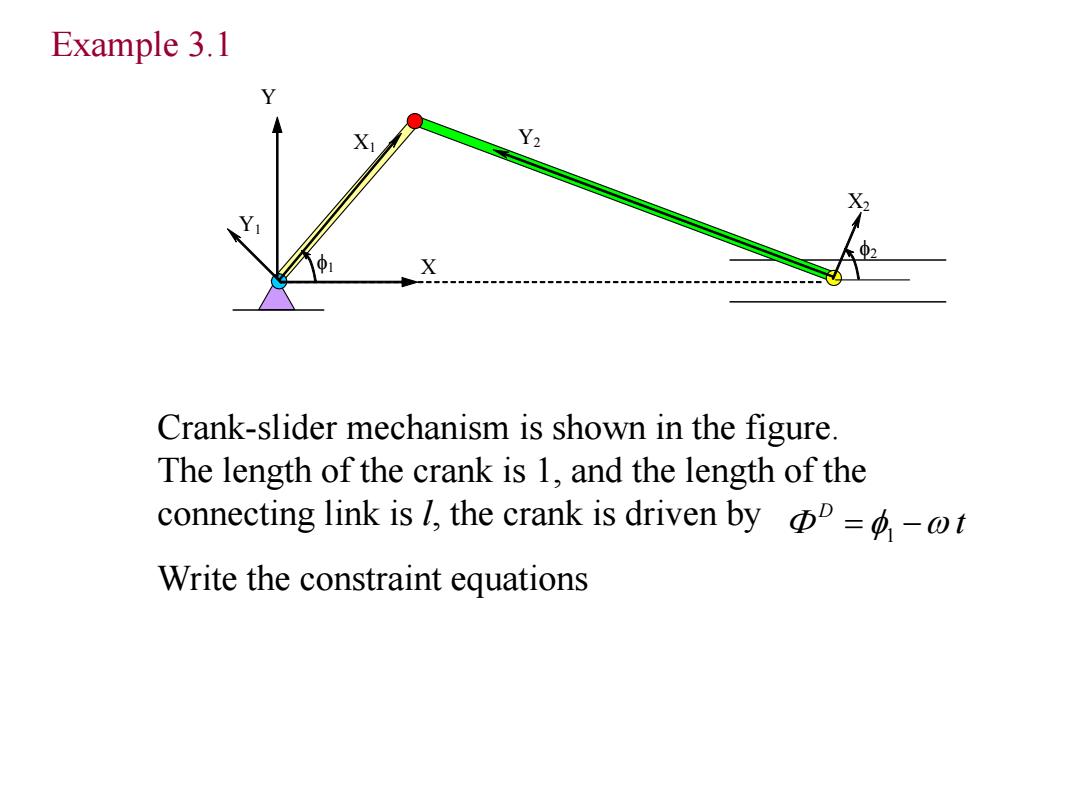
Example 3.1 Y Y2 X Crank-slider mechanism is shown in the figure. The length of the crank is 1,and the length of the connecting link is l,the crank is driven by=-t Write the constraint equations

1 X1 Y1 X2 Y2 2 X Y Example 3.1 Crank-slider mechanism is shown in the figure. The length of the crank is 1, and the length of the connecting link is l, the crank is driven by Write the constraint equations t D   1 

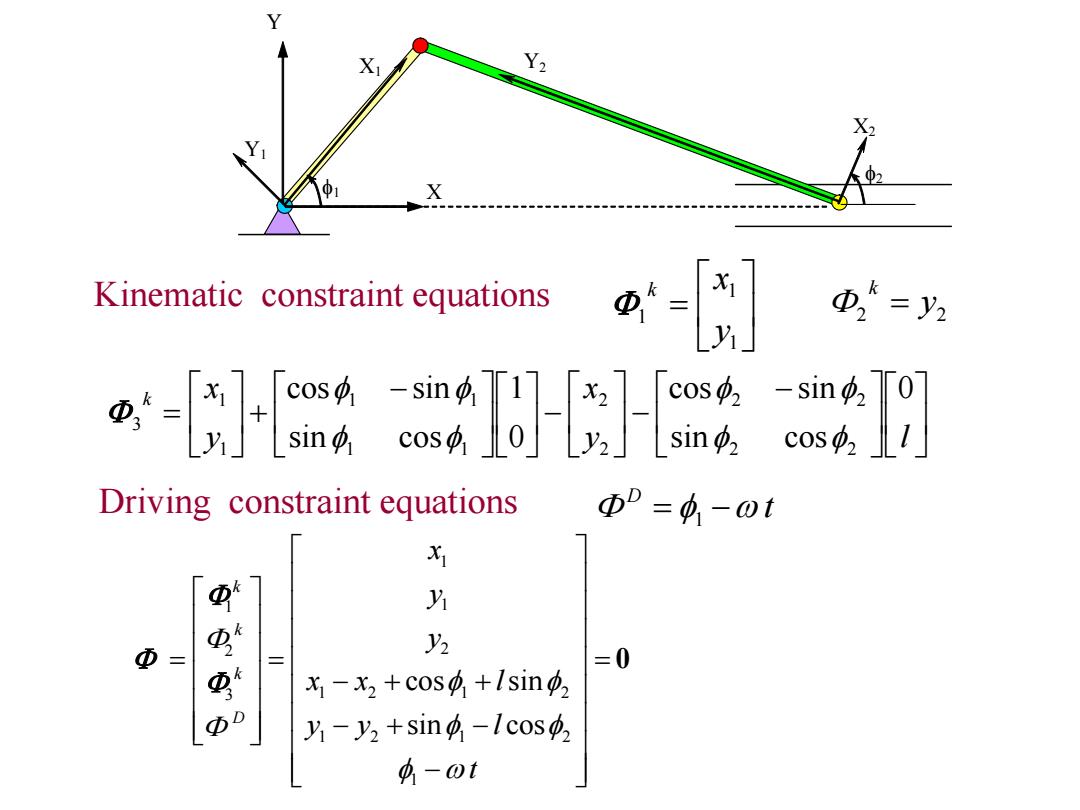
Y Y2 Kinematic constraint equations ,=2 cos2 Driving constraint equations Φ”=功-0t y Φ= y2 =0 -x2+cos +lsin y-y2+sin4-Icos中， 4-0t

1 X1 Y1 X2 Y2 2 X Y Kinematic constraint equations        1 1 1 y k x                                         y l x y x k 0 sin cos cos sin 0 1 sin cos cos sin 2 2 2 2 2 2 1 1 1 1 1 1 3          2 2 y k   t D   1  1 1 1 2 2 3 1 2 1 2 1 2 1 2 1 cos sin sin cos k k k D x y y x x l y y l t                                              0 Driving constraint equations

IfD,is nonsingular,.that isΦ，≠0 Time derivative of equations (g,t)=0I leads to (q,4,)=D,9+④，=0 更，9=-D,=v Time derivative of equations (g,t)=0 leads to 市=④，i+(中，)，1+D,i+亚g9+D:=0 Φ，i=Y Y=-(Φ，)m9-2Φ9-Φa TΦ nhx1 nhxnc

Time derivative of equations qt  0 leads to      0 t  q,q,t qq  Time derivative of equations q q,t  0 leads to         0     t t tt q q q q q q q q q q       ( )  q   q    t tt   ( qq)q q  2 q q  1 2 2           nh i tt t   1          nh i t t   nh nc j i q          q   nh nc nc k k k i j q q q                   1    q q  q q v q   t  If q is nonsingular, that is q  0

Example 3.2 Y X Y2 X Crank-slider mechanism is shown in the figure. The length of the crank is 1,and the length of the connecting link is l,write the velocity and acceleration constraint equations

1 X1 Y1 X2 Y2 2 X Y Example 3.2 Crank-slider mechanism is shown in the figure. The length of the crank is 1, and the length of the connecting link is l, write the velocity and acceleration constraint equations

Constraint equations X1 y Φ ] 2 =0,q= x-x2 +cos +lsin y-y2+sing -lcos 4,-ot Velocity constraint equations 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 二 =-①，=y 1 0 -sin o -1 lcosφ2 0 0 coS中， 0 -1 Isin2 0 0 0 0

Constraint equations                          2 2 2 1 1 1 1 1 2 1 2 1 2 1 2 2 1 1 sin cos cos sin          y x y x , t y y l x x l y y x D k 0 q   Velocity constraint equations q v q                     t y x y x l l          0 0 0 0 0 0 0 1 0 0 0 0 1 cos 0 1 sin 1 0 sin 1 0 cos 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 2 2 2 1 1 1 1 2 1 2       

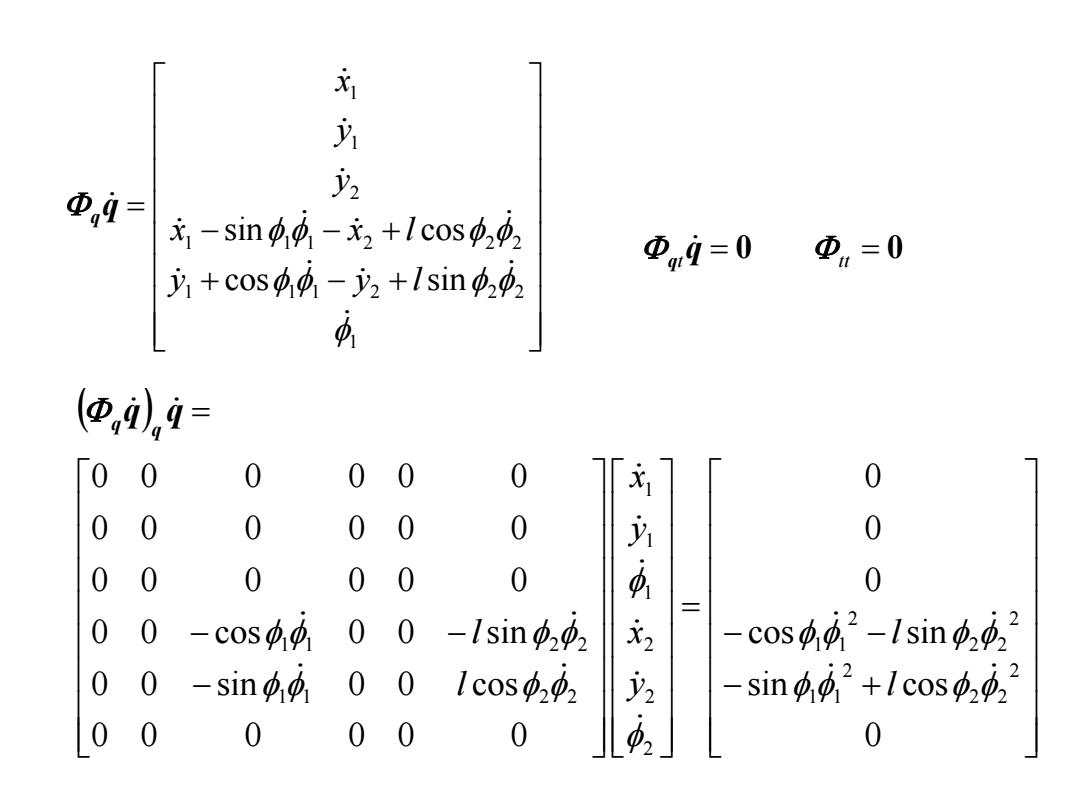
1 少 少2 中，1= 元-sin,4-元2+1cos, Φ，m9=0=0 +cos-i+lsin2 中 (，，9= 00 0 0 0 元1 0 0 0 0 00 0 0 00 0 00 0 0 00 -cos 0 0-Isin 元2 -cos2-Isin 00 -sin 00 Icos 少2 sin+lcos 0 0 0 00 0 可 0

           1 1 1 1 2 2 2 1 1 1 2 2 2 2 1 1 cos sin sin cos                       y y l x x l y y x qq                       0 sin cos cos sin 0 0 0 0 0 0 0 0 0 0 0 sin 0 0 cos 0 0 cos 0 0 sin 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 1 1 2 2 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 1 2 2                                   l l y x y x l l q q q q qtq  0 tt  0